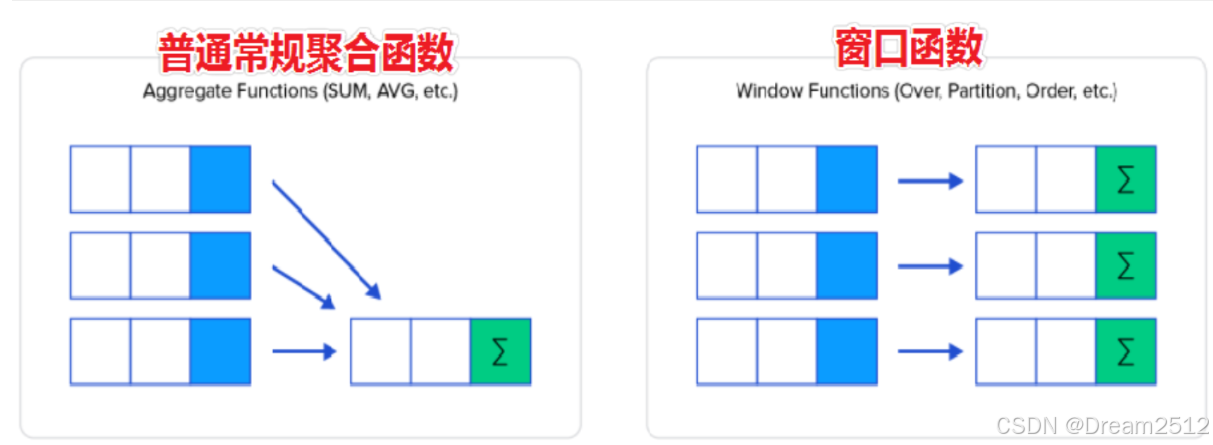
本文是对数学二线性代数基础进行总结,一些及极其简单的被省略了,代数的概念稀碎,不如高数关联性高,所以本文仅供参考,做题请从中筛选!
本文为初稿,后面会根据刷题和自己的理解继续更新
第一章:行列式:
基本概念:
link:
- 求n阶行列式:
- 余子式:
的余子式
是除去i行、j列的其余项组成的行列式
- 代数余子式:
- 按某行展开:
,元素乘其代数余子式,然后相加
记:
- 行列互换值不变
- 若某行元素全为0,行列式为0
- k*行列式=对行列式的一行都乘k倍
- 某行元素是两个数之和,可以拆成两个行列式之和
- 行列式两行互换,行列式变号
- 行列式中某行的k倍加到另一行,行列式不变
重要行列式:
link:
- 主对角线行列式:无论上下都是主对角线的乘积(这个概念对于分块矩阵也成立,称为拉普拉斯展开式)
- 副对角线行列式
副对角线元素的乘积(分块阵:
,AB为副对角线行列式乘积,m、n分别为A、B的阶数)
- 范德蒙德行列式:形如
 的行列式,其值为:
的行列式,其值为:
行列式计算:
link:
- 爪型行列式:利用斜爪消去竖爪或者横爪。然后展开
- 递推法:找规律,适用与宽对角类型的行列式行列式递推法1_哔哩哔哩_bilibili
- 抽象型行列式:性质、|AB|=|A||B|、将行列式拆分成两个行列式的乘积
- 余子式和代数余子式的线性组合:行列式按行(或按列)展开的“逆过程”。如:给|A|,和代数余子式的线性组合,把线性组合的系数换掉其按行展开的行,求出行列式就是代数余子式的和
- 求解n元非齐次方程组:克拉默法则:非齐次线性方程组的行列式(行列式不带等号右边的常数项),若不等于0,则方程组存在唯一解且解为
,
是常数项(等号右边的值
)替换第i列得到的行列式。
第二章:矩阵:
矩阵基本运算:
link:
- 不满足交换律
- 加法:每项相加;数乘:每项都乘
- 转置矩阵的性质:
相当重要
特殊矩阵:
link:
- 数量矩阵:k倍的单位矩阵
- 对称矩阵:满足条件
的矩阵称为对称矩阵
- 反对称矩阵:满足条件
,对角线为0,
- 分块矩阵:比较特殊的就是分块矩阵的n次幂
、求逆:
、
- 正交矩阵:
A的行(列)向量是规范正交基(正交的长度为单位1的向量)。
矩阵的逆
link:
- 本质:定义:AB=BA=E,则B为A的逆
- 可逆的充要条件是:
,可以把-1理解成负一次方:
,或者就是,把A做的变换反向变回去
- 重要性质:
、
、
- 求逆矩阵:定义法(AB=BA=E,
)、用伴随矩阵、初等变换求逆矩阵
伴随矩阵
link:
- 本质:定义:由A的代数余子式构成的矩阵
、
、
、
、
- 求逆矩阵的公式:
- 求伴随矩阵:定义法、用逆矩阵求伴随
初等矩阵:
link:
- 本质:对另一个矩阵进行初等变换,初等变换包括:数乘、互换、倍加
- 初等矩阵都可逆,逆矩阵也为初等矩阵(后面可以看一下初等变换逆前后对另一个矩阵的影响的变化)
- 可逆矩阵可表示为有限个初等矩阵的乘积。
- 对A作初等行变换,相当于左乘初等矩阵,列则是右。
- 初等变换求逆矩阵
矩阵方程:
,类似可自行推理
等价矩阵和等价标准型:
,P、Q为初等矩阵,也就是说,A通过初等变换可以变成B,则A和B等价。将其化为
,r为矩阵的秩。这个矩阵为等价标准型。
- 求可逆矩阵P:1、单个,把A化到B的过程每次行变换的矩阵相乘即可。2、求所有的可逆矩阵P:第四讲方程组求解再来看????
矩阵的秩:
- 本质:定义:存在k阶子式子不为0,任意k+1阶子式全为0,矩阵的秩r(A)=k。
- k是A的线性无关向量的个数;k个线性无关的向量,任意k+1个向量线性相关。
- 如何理解线性相关和线性无关:线性无关的向量撑起“整个空间”,线性相关的则是由这些线性无关向量表示,“躺平”在这个空间里。
- 重要式子:
、
、
、
、
、
、
、
第三章:向量组:
link:
- 正交向量:
,本质是垂直向量
- 向量的模:
,二维向量为例好记
- 标准正交基:本质就是相互垂直的单位向量组
- 线性无关:向量组中的每个向量都是“基础”的,它们独立存在,没有多余的部分
- 线性相关:向量组中有一些向量是“多余的”,可以由其他向量通过线性组合得到(存在不全为0的数,使
成立,其中k为0的就是多余的向量)
线性相关、线性无关
link:
判定线性相关的定理:
- 线性相关<=>向量组中,至少有一个向量可由其余的向量线性表示。(本质是存在非0的k),逆否命题:线性无关<=>向量中任何向量都不能由其余向量表示(本质不存在非0的k)
- 向量组a线性无关,a加一个向量
后线性相关,则
可由向量组a线性表示且唯一。(本质是引入了冗余向量)
- 大向量组b可由小a线性表示(大小体现在列),则向量组b线性相关。(本质:b 中所有向量实际上都“依赖”于 a)
- m(m列)个n(行)维向量组线性相关<=>其所构成的齐次线性方程组=0,有非零解<=>构成的矩阵的秩<m(列数)(本质:把方程列出来化简之后就是线性相关的定义,若有非零解就是k不全为0;m-秩=自由度,存在自由度,使方程=0)等价就是:线性无关充要条件是齐次方程组只有零解
可由向量组a表示<=>非齐次线性方程组=
有解<=>r([a,
])=r([a]) (本质:
在a的空间内,可由a表示)
- 如果向量组a一部分线性相关,则整个向量组线性相关,(小部分就能概括整个空间,则其余的都是多余向量)逆否命题:如果a向量无关,则任何一部分向量组都线性无关。
- 如果n维向量组a线性无关,则向量组添加m个分量得到的向量组(m+n)维也是线性无关。(添加的分量,是独立的信息,没有引入与原来a线性相关的冗余)逆否命题:a线性相关,去掉若干分类后也是线性相关。
- 总结:判断能不能线性表示,就看添加后是否多一维(秩),如果向量为撑起空间的向量,则不能被线性表示,如果向量不是撑起空间的向量,则可以被线性表示
记:
- 自由度:就是对秩展成的空间的约束
极大线性无关组
link:
- 本质:向量组中撑起空间的那几个向量的集合
- 求极大线性无关组用进行初等行变换,找出和矩阵秩相同的子矩阵就是(不唯一)
- 也就是说,求极大线性无关组可以作为空间的基向量,表示其他向量。那怎么表示其他向量呢:用矩阵乘法,基向量*倍数矩阵。
等价向量组:
link:
- 本质:两个向量组可以相互线性表示(同一个空间中的同一个子空间,只是使用的基向量不同),记为
- 等价向量组有传递性、对称性
- 若
<=>r(a)=r(B)=r(A,B)(三秩相同)
向量组的秩:
link:
- 三秩相等:r(A)=A的行秩=A的列秩
- 等价向量组=>秩相等
- 对A进行初等行变换后变为B,A、B的行向量是等价向量组
- 向量组A、B,若A中向的向量均可由B线性表示,则r(A)<=r(B)(A 的向量组实际上“依赖于” B 的向量组,说明 A 张成的子空间是 B 张成空间的子空间)
- r(A+B)<=r(A,B)<=r(A)+r(B)
第四章:线性方程组:
齐次线性方程组:
- r(A)=n,n为未知数的数量,此时有唯一0解,(此时,向量组为线性无关,只有x全为0的时候成立)
- r(A)=r<n,有非零解(无穷多个),且有n-r个线性无关解(自由度)(基础空间r+约束(自由度)=总维度n,)。
- 求解方法:1、行变换化为行阶梯型矩阵(方便看秩)。2、找出一个秩为r的子矩阵,其余位置为自由变量(明确自由变量)。3、设基础解系个数为n-r。4、设解中自由变量的位置为任意值(方便解题就行,一般是0或1),然后用A的每非0行和基础解系相乘,求出基础解系所有项。5、k*基础解系然后相加即可。
- 基础解系的理解:秩组成了基本的空间,如三维,自由项就是在三维上开辟一个二维的子空间(通过原点的线性子空间),这个子空间由基础解系描述
非齐次线性方程组:
为A的增广矩阵。
,方程无解(说明增广矩阵引入了新的独立方向,B不在A的空间内)
方程有唯一解(B在A内,没有自由项,所以解空间被完全限制,只要一个)
,方程有无穷多解
- 基础解系的理解:与非齐次的相同,但其描述的是偏移的线性子空间,与一阶的通过原点的不同。
- 求解方法:1、求出齐次方程通解,2、求出特解(设一个特解,选出秩相同的子矩阵,令自由变量全为0,带入行求出其他值)3、解=通解+特解
公共解:
- A与B的公共解:
,其实就是求通解的公共部分
同解方程组:
- A与B有完全相同的解
(三秩相同)
第五章:特征值与特征向量
矩阵的特征值和特征向量:
link:
- 本质:矩阵A对这个特殊的向量的变换就是λ,而这个特殊的向量就是特征向量
,
为特征值<=>方程有非零解<=>所以
(这个叫做特征方程,可求出
的n个解)。(求这个
需要做多项式除法)
- 若
为A的n个 特征值,
,
是A的属于
的特征向量<=>
是
的解
- k重特征值
至多只有k个线性无关的特征向量(k重特征值,是A对多个不同的k个特征向量有相同的作用效果)(特征值的“重数”表示矩阵 A 对某些方向(特征向量)的作用是重复的,但这些方向独立的最大数量(几何自由度)由重数 k 限制)其实跟没说一样,就是说当k个重复特征值的时候,仍可以有k个线性无关向量,只是提供一个上限,提示一下比k少的可以有。
- 若n个特征向量是A的属于不同特征值的特征向量,则这n个特征向量线性无关(线性相关的特征向量,A的特征值一定相同,而线性无关的可以相同也可以不同)
- 若
为A的属于同一(不同)特征值
的特征向量,则
仍是(不是)A的属于特征值
的特征向量(线性子空间的任意线性组合仍然属于这个子空间)
- 常规矩阵的特征值和特征向量

相似矩阵:
link:
,则AB相似记为A~B,这个相似有传递性
- 相似矩阵的必要性:|A|=|B|、r(A)=r(B)、tr(A)=tr(B)、
、
、A,B的各阶主子式之和分别相等
- A~B则
、
、
。以上结论A到B的手段与其变化后A到B的手段相同;
。
- 若A~C,B~D则
- 如何求相似:定义、传递性、必要性反正不相似
相似对角化:
- 本质:
,
为对角矩阵,则A可相似对角化,
是A的相似标准型
- 可相似对角化的充要条件:n阶矩阵A有n个线性无关的特征向量。(A对应每个k重特征值都有k个线性无关的特征向量)
- 可相似对角化的充分条件:n阶矩阵有n个不同的特征值;n阶矩阵为实对称矩阵(满秩)
- 计算:
- 求可逆阵P:1、求特征值,2、求特征向量,3、把向量按列排就是P
- 由特征值、特征向量反推A:
实对称矩阵的相似对角化:
link:
- 对称阵A的不同特征值的特征向量相互正交
- 利用
的性质推出:
- 求实对称矩阵的相似对角化的基本步骤是:1、求特征值,2、求特征向量,3、将特征向量正交化(why:因为要求正交矩阵Q),4、按列排就是Q
- 施密特正交化公式(将非正交积化为正交积):

第六章:二次型:
二次型的定义:
link:
- 本质:就是个二元齐次多项式f(x),写成
 的形式,用矩阵A表示。A为f(x)的二次型矩阵。
的形式,用矩阵A表示。A为f(x)的二次型矩阵。
合同变换:
link:
- 本质:把x换成y,把一个二次型(
)通过线性变换化为另一个二次型(
),A和B的关系 .若存在可逆矩阵C使
。则
。(从表达式A表示,到表达式B表示(换系))
- 合同必等价、对称矩阵合同也是对称矩阵
- 合同标准型:没有交叉项,只有平方项
- 规范型:把标准型的系数都化为1,0,-1
- 定理:1、任何实对称矩阵A(任何二次型),必存在可逆矩阵C,使得:
(对角阵,且为规范型)2、扩展到正交变换Q,
。
- 惯性定理:正系数(正惯性指数)和负系数(负惯性指数)的个数是不变的。合同变换下的不变量就是惯性指数
- 秩r=正惯性指数+负惯性指数
- 合同的充要条件:有相同的正负惯性指数;
- 在对称条件下,相似一定合同
- 合同和相似的区别:??
- 配方法化二次型:1、把二次型化成
的形式,2、令y1,y2,y3等于平方项内的x的和,3、解出x=y1+...,也就是x=Cy,4、然后换元带入,把二次型变为y的标准型,5、求出|C|不为0则可以做可逆线性变换。
正定二次型:
- 正定二次型<=>
<=>正惯性指数p=n<=>存在可逆矩阵D,
<=>A=E<=>A的特征值全部>0<=>A的全部顺序主子式均大于0
- 顺序主子式:看图

- 二次型正定的必要条件:系数都大于0;|A|>0