31. 873. 最长的斐波那契子序列的长度
题目:
如果序列
X_1, X_2, ..., X_n满足下列条件,就说它是 斐波那契式 的:
n >= 3- 对于所有
i + 2 <= n,都有X_i + X_{i+1} = X_{i+2}给定一个严格递增的正整数数组形成序列 arr ,找到 arr 中最长的斐波那契式的子序列的长度。如果一个不存在,返回 0 。
(回想一下,子序列是从原序列 arr 中派生出来的,它从 arr 中删掉任意数量的元素(也可以不删),而不改变其余元素的顺序。例如,
[3, 5, 8]是[3, 4, 5, 6, 7, 8]的一个子序列)
题目链接
873. 最长的斐波那契子序列的长度 - 力扣(LeetCode)
画图分析
代码
class Solution { public: int lenLongestFibSubseq(vector<int>& arr) { int n = arr.size(); vector<vector<int>>dp(n,vector<int>(n,0)); map<int,int>hash; hash.insert({arr[0],0}); int len = 0; for(int j = 2;j < n;j++) { hash.insert({arr[j - 1],j - 1}); for(int i = j - 1;i >= 1;i--) { int x = arr[j] - arr[i]; if(hash.count(x) && hash[x] < i) { dp[i][j] = max(dp[i][j],dp[hash[x]][i] + 1); len = max(len,dp[i][j]); } } } if(len == 0) { return 0; } return len + 2; } };
32. 1027. 最长等差数列
题目:
给你一个整数数组
nums,返回nums中最长等差子序列的长度。回想一下,
nums的子序列是一个列表nums[i1], nums[i2], ..., nums[ik],且0 <= i1 < i2 < ... < ik <= nums.length - 1。并且如果seq[i+1] - seq[i](0 <= i < seq.length - 1) 的值都相同,那么序列seq是等差的。
题目链接
1027. 最长等差数列 - 力扣(LeetCode)
文字分析
主要解题思路参考 873.最长的斐波那契子序列的长度
同样的我们可以通过两个元素,反推前面一个数
注意:
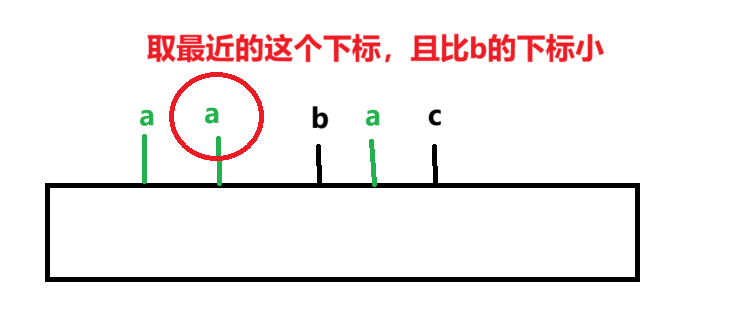
1. 这道题目没有规定一个数不能重复出现,所以判断前一个数是否存在,得到的下标有多个,要得到最大的子序列,下标应该最近的那个(实现这一点,hash表可以采取覆盖式的更新下标)
2. 这里的最长长度至少是2,任意两个数也构成定差子序列
代码
class Solution { public: int longestArithSeqLength(vector<int>& nums) { map<int,int> hash; hash[nums[0]] = 0; int n = nums.size(); int Max = 2; vector<vector<int>> dp(n,vector<int>(n,2)); for(int i = 1;i < n;i++) { for(int j = i + 1;j < n;j++) { int a = 2 * nums[i] - nums[j]; if(hash.count(a)) { dp[i][j] = dp[hash[a]][i] + 1; } Max = max(Max,dp[i][j]); } hash[nums[i]] = i; //更新下标 } return Max; } };
33. 446. 等差数列划分2 -- 子序列
题目:
给你一个整数数组
nums,返回nums中所有 等差子序列 的数目。如果一个序列中 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该序列为等差序列。
- 例如,
[1, 3, 5, 7, 9]、[7, 7, 7, 7]和[3, -1, -5, -9]都是等差序列。- 再例如,
[1, 1, 2, 5, 7]不是等差序列。数组中的子序列是从数组中删除一些元素(也可能不删除)得到的一个序列。
- 例如,
[2,5,10]是[1,2,1,2,4,1,5,10]的一个子序列。题目数据保证答案是一个 32-bit 整数。
题目链接
446. 等差数列划分 II - 子序列 - 力扣(LeetCode)
文字分析
这道题和 1027.最长等差数列 相似,唯一最大的不同是:
由题目的示例2可知,子序列可以重复多算
注意:
这道题算出来的一些数很可能会越界,得用 long long 存储
代码
class Solution { public: int numberOfArithmeticSlices(vector<int>& nums) { unordered_map<long long, vector<int>> hash; int n = nums.size(); vector<vector<long long>>dp(n, vector<long long>(n, 0)); //模拟哈希桶 int len = 0; hash[nums[0]].push_back(0); for (int j = 2; j < n; j++) { for (int i = j - 1; i >= 1; i--) { long long x = (long long)2 * nums[i] - nums[j]; //不做强转,数据会溢出 if (hash.count(x)) { for (int e : hash[x]) { if (e < i) { dp[i][j] += (dp[e][i] + 1); } } len += dp[i][j]; } } hash[nums[j - 1]].push_back(j - 1); } return len; } };