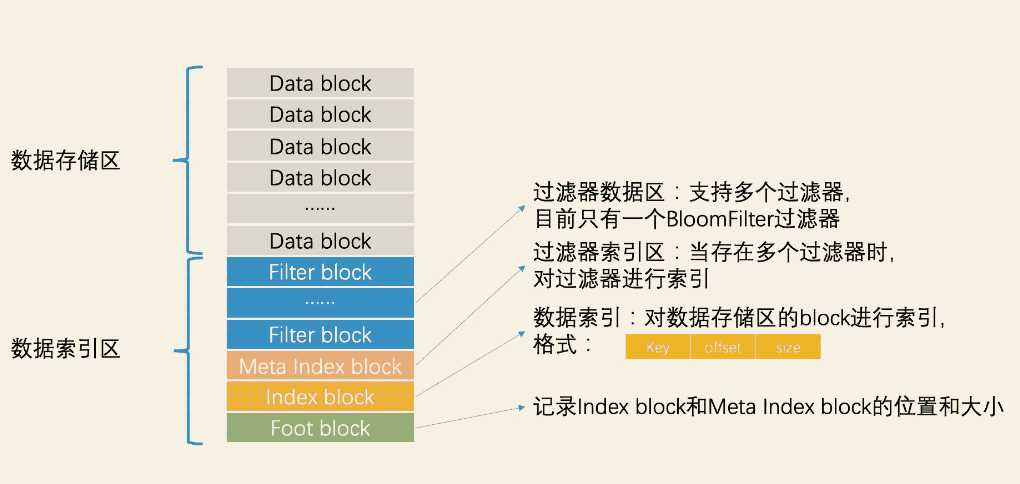
学习资料:bilibili 西湖大学赵世钰老师的【强化学习的数学原理】课程。链接:强化学习的数学原理 西湖大学 赵世钰
文章目录
- 一、为什么return重要?如何计算return?
- 二、state value的定义
- 三、Bellman公式的详细推导
- 四、公式向量形式与求解
- 五、Action value的定义
- 六、本节课内容summary
一、为什么return重要?如何计算return?

上面三幅图分别代表三个策略,从直观上我们可以判断,左边策略是最好的,因为它不经过forbidden area就能到达终点;中间策略是最差的,因为它经过了forbidden area;右边策略是既不好也不差的,因为它有一定的概率经过forbioden area到达终点,也有一定的概率不经过forbidden area而直接到达终点。
那么,该如何用数学的方式来直观地表达不同策略的优劣呢?答案就是用return来表示。
对于左边策略,计算return1:

对于中间策略,计算return2:

对于右边策略,计算return3:
严格来说这个return3已经不再是return的概念了,因为return的定义表明,return是根据一个轨迹trajectory计算出来的,而这里的return3是根据两个轨迹共同计算出来的。这里的return3其实是后面state value的概念。

得出结果,return1>return3>return2。所以,可以用return来直观地表达不同策略的优劣。
那么该如何计算return呢?
请看下图推导过程。发现从不同状态出发得到的return,依赖于从其他状态得到的return。这个idea在强化学习中被称为bootstrapping,常常指从自己出发,不断迭代所得到的结果。因此,下面有4个未知数v1-v4,同时也有4个方程,所以可以使用线性代数的方法解出未知数。


上图中的式子其实就是贝尔曼公式,但只适用于确定性问题。上面这个式子告诉我们:一个状态的value实际上依赖于其他状态的value。
下图是一个应用的小例子,可以辅助理解。

二、state value的定义
下图介绍了一些符号。
注意:
(1)
R
t
+
1
R_{t+1}
Rt+1其实也可以写成
R
t
R_{t}
Rt,就是说在状态
S
t
S_{t}
St下选择了动作
A
t
A_{t}
At,得到了奖励
R
t
R_{t}
Rt。这是说得通的,但一般都习惯性地写成
R
t
+
1
R_{t+1}
Rt+1。
(2)S、A、R都是随机变量,所以可以对它们求期望等操作。
(3)这个single-step process是由概率分布决定的。(见下图三行蓝字)
(4)我们假设我们已知模型,即已知概率分布。

考虑下面的trajectory。在状态
S
t
S_{t}
St下选择了动作
A
t
A_{t}
At,得到了奖励
R
t
R_{t}
Rt,转移到状态
S
t
+
1
S_{t+1}
St+1,再选择动作
A
t
+
1
A_{t+1}
At+1……对这一个trajectory,可以求discounted return,结果用
G
t
G_t
Gt表示。

有了上面的铺垫,下面来讨论state value。下图是对state value的定义。
G
t
G_t
Gt表示一个trajectory的discounted return,而state value就是
G
t
G_t
Gt的期望值/平均值,这个期望值是在当前状态s下来计算的,也就是对多个trajectory的平均。
state value表示为
v
π
(
s
)
v_π(s)
vπ(s),也可以表示为
v
(
s
,
π
)
v(s, π)
v(s,π)。
注意:
(1)
v
π
(
s
)
v_π(s)
vπ(s)是关于s的一个函数,所以从不同的状态s出发,会得到不同的trajectory,因而discounted return也不同,期望值也不同。
(2)
v
π
(
s
)
v_π(s)
vπ(s)是一个与策略相关的函数。不同的策略也会带来不同的state value。
(3)
v
π
(
s
)
v_π(s)
vπ(s)代表状态s的价值,如果某一个状态s的state value更大,则代表从该状态s出发,可能得到更多的return。
(4)return 和 state value 有什么区别?return是针对单个trajectory求出来的奖励,而state value是对多个trajectory得到的奖励再求平均值。

例:针对图中3个策略分别计算其state value。

三、Bellman公式的详细推导
下图回顾了trajectory的含义,以及
G
t
G_t
Gt可以被写成当前的即时回报
R
t
+
1
R_{t+1}
Rt+1与未来回报
G
t
+
1
G_{t+1}
Gt+1的和。然后我们再看state value的定义,state value本质上是对多个trajectory的累计回报求均值,而求均值这个操作是可以被拆分的,因此可以转化成下图中蓝字所呈现的形式。其中,
E
[
R
t
+
1
∣
S
t
=
s
]
E[R_{t+1}|S_t=s]
E[Rt+1∣St=s] 表示在状态s下获得的即时回报
R
t
+
1
R_{t+1}
Rt+1的期望,
E
[
G
t
+
1
∣
S
t
=
s
]
E[G_{t+1}|S_t=s]
E[Gt+1∣St=s] 表示在状态s下,从下一个状态出发,走过多个trajectory的累计回报的均值。下面,分别计算
E
[
R
t
+
1
∣
S
t
=
s
]
E[R_{t+1}|S_t=s]
E[Rt+1∣St=s] 和
E
[
G
t
+
1
∣
S
t
=
s
]
E[G_{t+1}|S_t=s]
E[Gt+1∣St=s] 。

首先,计算
E
[
R
t
+
1
∣
S
t
=
s
]
E[R_{t+1}|S_t=s]
E[Rt+1∣St=s]。
E
[
R
t
+
1
∣
S
t
=
s
]
E[R_{t+1}|S_t=s]
E[Rt+1∣St=s] 表示在状态s下获得的即时回报
R
t
+
1
R_{t+1}
Rt+1的期望。在状态s下,我可以选择动作
a
1
a_1
a1,
a
2
a_2
a2,
a
3
a_3
a3…,而对于其中任意一个动作
a
i
a_i
ai,都有可能带来不同的即时回报
r
1
r_1
r1,
r
2
r_2
r2,
r
3
r_3
r3…,所有这些即时回报的均值就是我们要求的
R
t
+
1
R_{t+1}
Rt+1。所以,要求
E
[
R
t
+
1
∣
S
t
=
s
]
E[R_{t+1}|S_t=s]
E[Rt+1∣St=s],先算在状态s下可能选择哪些动作a,以及选择动作a的概率
π
(
a
∣
s
)
π(a|s)
π(a∣s)有多大,如下图推导过程中第1行所示。然后再算
E
[
R
t
+
1
∣
S
t
=
s
,
A
t
=
a
]
E[R_{t+1}|S_t=s, A_t=a]
E[Rt+1∣St=s,At=a],即在状态s的情况下,选择动作a可能会带来哪些回报r,带来回报r的概率
p
(
r
∣
s
,
a
)
p(r|s,a)
p(r∣s,a) 有多大。

然后,计算 E [ G t + 1 ∣ S t = s ] E[G_{t+1}|S_t=s] E[Gt+1∣St=s] 。 E [ G t + 1 ∣ S t = s ] E[G_{t+1}|S_t=s] E[Gt+1∣St=s] 表示在状态s下,从下一个状态出发,走过多个trajectory的累计回报的均值。
先看下面推导过程中的第1行。要算 E [ G t + 1 ∣ S t = s ] E[G_{t+1}|S_t=s] E[Gt+1∣St=s],也就是要算从当前状态s出发,能够到达哪些状态?这些状态的每一个 G t + 1 G_{t+1} Gt+1 分别是什么?把所有的 G t + 1 G_{t+1} Gt+1 都求出来,再取一个均值,就得到了 E [ G t + 1 ∣ S t = s ] E[G_{t+1}|S_t=s] E[Gt+1∣St=s]。第1行中的 p ( s ′ ∣ s ) p(s'|s) p(s′∣s) 表示从当前状态s出发,转移到状态s’的概率。 E [ G t + 1 ∣ S t = s , S t + 1 = s ′ ] E[G_{t+1}|S_t=s, S_{t+1}=s'] E[Gt+1∣St=s,St+1=s′] 表示当前状态为s,下一个状态为s’时所获得的state value。
再看下面推导过程中的第2行。第2行其实是对第1行进行了简化。根据马尔科夫决策过程的无记忆性(memoryless property),在t+1时刻所获得的累计回报return G t + 1 G_{t+1} Gt+1 只和 t+1 时刻的状态有关,和 t 时刻的状态是没关系的,所以可以去掉公式中的 S t = s S_t=s St=s 部分。
再看下面推导过程中的第3行。 E [ G t + 1 ∣ S t + 1 = s ′ ] E[G_{t+1}|S_{t+1}=s'] E[Gt+1∣St+1=s′] 其实就是 v π ( s ′ ) v_π(s') vπ(s′) ,可以再进一步简化。
再看下面推导过程中的第4行。
p
(
s
′
∣
s
)
p(s'|s)
p(s′∣s) 表示从当前状态s出发,转移到状态s’的概率,可对其进一步扩展。表示从当前状态s出发,选择状态a,转移到状态s’的概率
p
(
s
′
∣
s
,
a
)
p(s'|s, a)
p(s′∣s,a),再乘上从当前状态s出发,选择动作a的概率
π
(
a
∣
s
)
π(a|s)
π(a∣s)。

现在,可以给出贝尔曼公式的表达式。

Highlights:
(1)贝尔曼公式描述了不同状态的state value之间的关系。比如,在上式中,状态s的state value 和状态s’的state value,两者的关系就可以通过贝尔曼公式表达出来。
(2)公式包含两项,一部分是即时奖励,一部分是未来奖励。
(3)这个式子不仅仅针对一个状态s,对于状态空间S中的任意一个状态s,上述式子都是成立的。所以如果有n个状态,就对应着n个式子。
(4)
v
π
(
s
)
v_π(s)
vπ(s) 的计算可以通过bootstrapping的方法。(n个方程,n个未知数,联立求解。)
(5)贝尔曼公式是依赖于policy
π
(
a
∣
s
)
π(a|s)
π(a∣s) 的。所以对于任何一个policy
π
(
a
∣
s
)
π(a|s)
π(a∣s) ,如果把state value计算出来,那也就能够评判这个policy
π
(
a
∣
s
)
π(a|s)
π(a∣s) 的好坏了。这个过程就是policy evaluation。
(6)
p
(
s
′
∣
s
,
a
)
p(s'|s, a)
p(s′∣s,a) 和
p
(
r
∣
s
,
a
)
p(r|s, a)
p(r∣s,a) 被称作dynamic model。在本节学习过程中,假设这个model是已知的。若不知道这个model,仍然可以计算出state value,这是model free reinforcement learning相关的算法。
下面是一个小练习。参考下面这张图,根据贝尔曼公式,写出这张图对应的贝尔曼方程。得到最下面的结果。其实最终结果也可以通过直接手写方便地得到,0表示即时奖励(r=0),
v
π
(
s
3
)
v_π(s_3)
vπ(s3)表示未来的奖励,再乘上一个折扣因子γ即可。

四、公式向量形式与求解
把贝尔曼公式转换成 Matrix-vector form,更加有利于我们去求解。先对贝尔曼公式进行烟花,转换成下图所示的“即时奖励+未来奖励”的形式。

为了识别不同的状态,在下图的贝尔曼公式中,给状态标上号。如下图所示,
v
π
(
s
i
)
v_{\pi}(s_i)
vπ(si)等于即时奖励
r
Π
(
s
i
)
r_Π(s_i)
rΠ(si)再加上未来奖励。从状态
s
i
s_i
si 跳转到下一个状态有j中可能性,用转移概率乘上每个状态的state value,就是未来奖励。这个公式可以简化成下图中蓝字的形式。

举一个具体的例子,当只有4种状态的时候,贝尔曼公式可以写成下图的矩阵表示。

这是另一个例子:

为什么要求解state value?
求解出state value后,方便我们去评价一个policy究竟是好还是坏。这也被称作policy evaluation。
如何求解state value?

策略一: closed-form solution
但是,如果状态空间比较大,那么矩阵的维数也比较大,不方便求解。

策略二: iterative solution
在k=0时,假设对于所有的状态s,
v
π
(
s
)
v_{\pi}(s)
vπ(s) 都等于0,把0带入到贝尔曼公式进行计算,得到k=1时的所有
v
π
(
s
)
v_{\pi}(s)
vπ(s) , 再把所有k=1时的
v
π
(
s
)
v_{\pi}(s)
vπ(s) 代入到贝尔曼公式进行计算,得到k=2时的所有
v
π
(
s
)
v_{\pi}(s)
vπ(s) …… 一直以此类推下去。可以证明,当k趋向于 无穷的时候,
v
k
v_k
vk 会收敛到
v
π
v_\pi
vπ (证明过程略)。

下图展示了两个比较好的策略所计算出的state value.可以发现, (1)靠近target area的格子,它们的state value都比较大,远离target area的格子,它们的state value都比较小;(2)仔细观察能发现,上下两个策略略有不同,但他们算出来的state value都是一样的。所以即使策略不同,算出来的state value也可能相同。

下面是两个比较差的策略。格子的state value基本都是负值。因此可以更直观地发现,可以通过计算state value来评判一个policy是不是好。

五、Action value的定义
state value 和 action value有什么区别和联系呢?
state value 指的是从一个状态出发所得到的average return;
action value 指的是从一个状态出发,并且选择了一个action,所得到的average return。
为什么要关注action value?
因为强化学习的目标是得到一个最优策略,策略实际上是由一系列的action组成(在哪个状态应该选择什么样的action)。那么,对于若干可选的action,我可以选择哪些呢?这就需要根据action value来做判断。

下图是关于action value的定义。有两点需要注意:
(1)action value 是一个关于状态-动作对
(
s
,
a
)
(s, a)
(s,a) 的函数。
(2)action value 的值依赖于策略
π
{\pi}
π。

在数学上,action value 和 state value 有哪些联系?
本节开头种提到,state value 和 action value 实际上就差了一个动作a。所以 state value 可以写成 action value 再乘上
π
(
a
∣
s
)
\pi(a|s)
π(a∣s) 的形式。如下图所示。

根据之前的推导,贝尔曼公式可以写成下图公式(3)的形式。通过比较式(2)和式(3),可以推导出action value的表达式。如下图种式(4)所示。
公式(2)告诉我们,如果知道了action value,就可以算出state value。
公式(4)告诉我们,如果知道了state value,可以算出action value。

下图是一个例子,看图写action value。因为这个图比较简单,所以可以通过判断“即时奖励”和“未来奖励”的方式很快手写出来。


Highlights:
(1)action value是非常重要的,可以帮助我们确定该选择哪个action。
(2)如何计算action value?有两种方法。第一,可以先把state value都算出来,再套公式计算action value。第二,可以通过数据的方式,不计算state value而直接计算出action value(未来会介绍)。
六、本节课内容summary