优化求解 | 非线性最小二乘优化器Ceres安装教程与应用案例

news2024/11/26 5:48:46

目录

  • 0 专栏介绍
  • 1 `Ceres`库介绍
  • 2 `Ceres`库安装
  • 3 `Ceres`库概念
    • 3.1 构建最小二乘问题
      • 3.1.1 残差块
      • 3.1.2 代价函数
    • 3.2 求解最小二乘问题
  • 4 `Ceres`库案例
    • 4.1 Powell函数优化
    • 4.2 非线性曲线拟合

0 专栏介绍

🔥课设、毕设、创新竞赛必备！🔥本专栏涉及更高阶的运动规划算法轨迹优化实战，包括：曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等)，每个算法都包含代码实现加深理解

🚀详情：运动规划实战进阶：轨迹优化篇

1 Ceres库介绍

Ceres是一个开源的 C++ 库，用于求解大规模非线性最小二乘问题。它非常适用于优化问题，尤其是涉及到参数估计、图像处理、机器学习、机器人学、计算机视觉和计算几何等领域的问题。Ceres的设计强调高效性、灵活性和易用性，支持高效求解带有复杂约束的最优化问题，具有很强的扩展性。

在这里插入图片描述

非线性最小二乘应用于图像配准

在这里插入图片描述

非线性最小二乘应用于位姿估计

为了更好地使用Ceres，首先得了解什么是最小二乘问题

最小二乘问题表述如下

min ⁡ x F ( x ) = 1 2 min ⁡ x ∑ i ρ i ( ∥ f i ( x ) ∥ 2 2 ) s . t .      l ≤ x ≤ u \min _{\boldsymbol{x}}F\left( \boldsymbol{x} \right) =\frac{1}{2}\min _{\boldsymbol{x }}\sum_{i}{\rho_i( \left\| f_i\left( \boldsymbol{x} \right) \right\| _{2}^{2})} \\ s.t.\ \ \ \ \boldsymbol{l} \le \boldsymbol{x} \le \boldsymbol{u} xmin​F(x)=21​xmin​i∑​ρi​(∥fi​(x)∥22​)s.t.    l≤x≤u

其中 ρ i ( ∥ f i ( x ) ∥ 2 2 ) \rho_i( \left\| f_i\left( \boldsymbol{x} \right) \right\| _{2}^{2}) ρi​(∥fi​(x)∥22​)称为残差块(residual block)，一个优化问题通常由多个残差块组成，每个残差块负责计算一个或多个残差； f i ( ⋅ ) f_i\left( \cdot \right) fi​(⋅)是代价函数， ρ i ( ⋅ ) \rho_i\left( \cdot \right) ρi​(⋅)是损失函数； x \boldsymbol{x} x是优化变量或称为参数块(parameter blocks)。

Ceres建模了上述有界非线性最小二乘问题，通过更新优化变量，使残差达到最小，此时的优化变量就是该问题的数值最优解

2 Ceres库安装

Ceres库的安装需要很多依赖项，比较繁琐。为了方便起见，本文采用Conan在不影响系统文件的情况下一键安装

Conan是一个开源的C/C++包管理器，类似于Python中的第三方管理Anaconda，开发人员可以通过Conan轻松地下载、构建、安装和管理各种C/C++库，并将它们集成到他们的项目中，加快构建过程，提高项目构建的效率。具体请参考Conan安装与C++第三方环境配置保姆级图文教程(附速查字典)

在这里插入图片描述
首先新建3rd目录，编写conanfile.py文件

from conan import ConanFile
from conan.tools.cmake import cmake_layout

class ExampleRecipe(ConanFile):
    settings = "os", "compiler", "build_type", "arch"
    generators = "CMakeDeps", "CMakeToolchain", "cmake_find_package", "cmake"
    
    def configure(self):
        self.options["ceres-solver"].shared = True
        self.options["ceres-solver"].use_glog = True
        self.options["glog"].shared = True
        self.options["glog"].with_threads = True
        self.options["gflags"].shared = True

    def requirements(self):
        self.requires("ceres-solver/1.14.0")

    def layout(self):
        cmake_layout(self)

接着只要在该目录启动终端运行

conan install . --output-folder=build --build=missing -s compiler.libcxx=libstdc++11

Conan会自动从云端拉取Ceres库所需要的依赖，并自动在本地编译

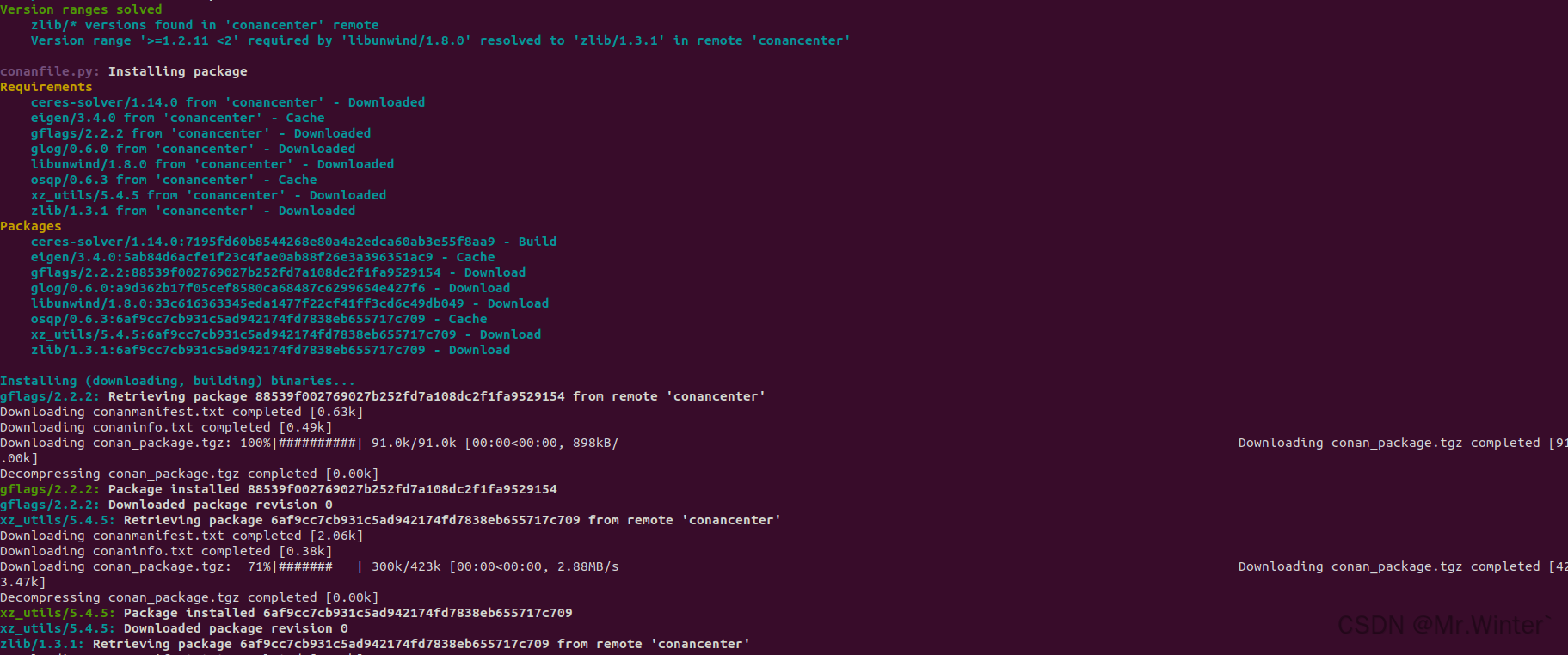
在这里插入图片描述
编译好的文件在~/.conan/data目录

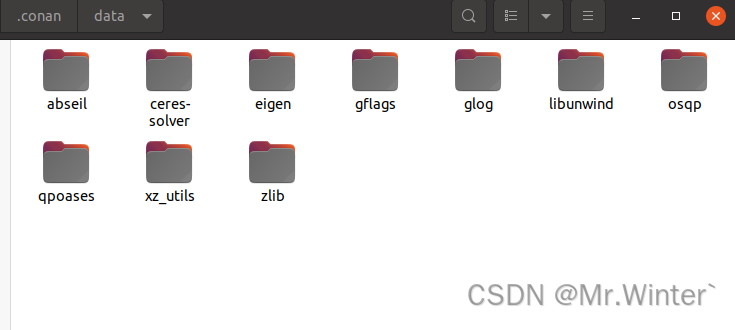
在这里插入图片描述

3 Ceres库概念

Ceres的求解过程包括构建最小二乘和求解最小二乘问题两部分

3.1 构建最小二乘问题

3.1.1 残差块

Ceres库通过向Ceres::Problem添加残差块构建最小二乘问题，因此其中最核心的函数为Problem::AddResidualBlock( )

ResidualBlockId Problem::AddResidualBlock(CostFunction *cost_function, 
										  LossFunction *loss_function, 
										  const vector<double *> parameter_blocks)
										  
ResidualBlockId Problem::AddResidualBlock(CostFunction *cost_function, 
										  LossFunction *loss_function,
										  double *x0, double *x1, ...)
  • 代价函数：包含了参数模块的维度信息，内部使用仿函数定义误差函数的计算方式，传入的参数模块需要和代价函数模块中定义的维数一致，维度不一致时程序会强制退出
  • 损失函数：用于处理参数中含有野值的情况，避免错误量测对估计的影响，常用参数包括HuberLoss、CauchyLoss等；该参数可以取nullptr，此时损失函数为单位函数。
  • 参数模块：待优化的参数，可一次性传入所有参数的指针容器vector<double*>或依次传入所有参数的指针double*。

3.1.2 代价函数

与其他非线性优化工具包一样，Ceres库的性能很大程度上依赖于导数计算的精度和效率。这部分工作在Ceres库中用CostFunction类封装，较为常用的包括以下三种：

  • 自动导数(AutoDiffCostFunction)：由Ceres库自行决定导数的计算方式，最常用的求导方式，其中的计算原理类似于深度学习框架中采用的计算图，几乎没有数值误差；
  • 数值导数(NumericDiffCostFunction)：由用户手动编写导数的数值求解形式，针对无法定义自动求导的模板仿函数的情况, 比如参数的估计调用了无法控制的库函数或外部函数，实现原理上通过有限差分实现导数的计算
  • 解析导数(Analytic Derivatives)：当导数存在闭合解析形式时使用，用于可基于CostFunciton基类自行编写；但由于需要自行管理残差和雅克比矩阵，除非闭合解具有具有明显的精度和效率优势，否则不建议使用

代价函数的定义采用仿函数，必须遵守一定的接口规范

考虑如下方程：
y = e a x 2 + b x + c + w \boldsymbol{y}=e^{a\boldsymbol{x}^2+b\boldsymbol{x}+c}+\boldsymbol{w} y=eax2+bx+c+w
其中 a a a、 b b b、 c c c是待估计的曲线参数， w \boldsymbol{w} w是高斯噪声，假设有 n n n个观测样本 ( x i , y i ) (x_i,y_i) (xi​,yi​)，希望根据这组样本得到最佳的曲线参数，构造如下的优化问题
F ( θ ) = min ⁡ 1 2 n ∑ i = 1 n ( y i − e a x i 2 + b x i + c ) 2 F(\boldsymbol{\theta})=\min \frac{1}{2n}\sum_{i=1}^{n}{(y_i-e^{ax_i^2+bx_i+c})^2} F(θ)=min2n1​i=1∑n​(yi​−eaxi2​+bxi​+c)2

此时代价函数定义为

struct ExponentialResidual
{
  ExponentialResidual(double x, double y) : x_(x), y_(y)
  {
  }
  template <typename T>
  bool operator()(const T* const a, const T* const b, const T* const c, T* residual) const
  {
    residual[0] = y_ - exp(a[0] * x_ * x_ + b[0] * x_ + c[0]);
    return true;
  }

private:
  const double x_;
  const double y_;
};

const double data[] = {...};
double a = 0, b = 0, c = 0;
problem.AddResidualBlock(new ceres::AutoDiffCostFunction<ExponentialResidual, 1, 1, 1, 1>(
                                 new ExponentialResidual(data[2 * i], data[2 * i + 1])),
                             nullptr, &a, &b, &c);

在CostFunction模板中：

  • 第一个参数FunctorType：表示代价函数的类型
  • 第二个参数kNumResiduals：表示代价函数的残差维度，如果代价函数是标量，则kNumResiduals是1；如果代价函数是向量（例如多个误差项的和），则kNumResiduals是该向量的维度
  • 后面若干参数kNumParameters：表示每个优化参数的维度，代价函数中有多少个输入的优化变量，就需要在模板里写多少个该参数

所以上面的引例也可以写为

struct ExponentialResidual
{
  ExponentialResidual(double x, double y) : x_(x), y_(y)
  {
  }
  template <typename T>
  bool operator()(const T* const params, T* residual) const
  {
    residual[0] = y_ - exp(params[0] * x_ * x_ + params[1] * x_ + params[2]);
    return true;
  }

private:
  const double x_;
  const double y_;
};

const double data[] = {...};
std::vector<double> params(3);
problem.AddResidualBlock(new ceres::AutoDiffCostFunction<ExponentialResidual, 1, 3>(
                                 new ExponentialResidual(data[2 * i], data[2 * i + 1])),
                             nullptr, params.data());

3.2 求解最小二乘问题

使用ceres::Solve进行求解，其函数原型如下：

void Solve(const Solver::Options& options, Problem* problem, Solver::Summary* summary)

其中

  • options：求解器的配置，求解的配置选项
  • problem：求解的问题，也即3.1节构建的最小二乘问题
  • summary：求解的优化信息，用于存储求解过程中的优化信息

对求解器可选的配置Solver::Options做如下说明：

  • minimizer_type：迭代的求解方式，可选如下：
    • TRUST_REGION：信赖域方式，默认值
    • LINEAR_SEARCH：线性搜索方法
  • trust_region_strategy_type：信赖域策略，可选如下：
    • LEVENBERG_MARQUARDT：列文伯格-马夸尔特方法，默认值
    • DOGLEG：狗腿法
  • linear_solver_type：求解线性方程组的方式
    • DENSE_QR：QR分解法，默认值，用于小规模最小二乘求解
    • DENSE_NORMAL_CHOLESKY和 SPARSE_NORMAL_CHOLESKY：CHolesky分解，用于有稀疏性的大规模非线性最小二乘求解
    • CGNR：共轭梯度法求解稀疏方程
    • DENSE_SCHUR和SPARSE_SCHUR：SCHUR分解，用于BA问题求解
    • ITERATIVE_SCHUR：共轭梯度SCHUR，用于求解BA问题
  • num_threads：求解使用的线程数
  • minimizer_progress_to_stdout：是否将优化信息输出至终端，默认为false。若设置为true输出根据迭代方法而输出不同：
    • 信赖域方法
      • cost：当前目标函数的数值
      • cost_change：当前参数变化量引起的目标函数变化
      • |gradient|：当前梯度的模长
      • |step|：参数变化量
      • tr_ratio：目标函数实际变化量和信赖域中目标函数变化量的比值
      • tr_radius：信赖域半径
      • ls_iter：线性求解器的迭代次数
      • iter_time：当前迭代耗时
      • total_time：优化总耗时
    • 线性搜索方法
      • f：当前目标函数的数值
      • d：当前参数变化量引起的目标函数变化
      • g：当前梯度的模长
      • h：参数变化量
      • s：线性搜索最优步长
      • it：当前迭代耗时
      • tt：优化总耗时

4 Ceres库案例

4.1 Powell函数优化

Powell函数是数值优化实验中常用的测试函数，其表达式为

min ⁡ x 1 2 ∥ F ( x ) ∥ 2 \min _{\boldsymbol{x}} \frac{1}{2}\|F(\boldsymbol{x})\|^2 xmin​21​∥F(x)∥2

其中 x = [ x 1 , x 2 , x 3 , x 4 ] T \boldsymbol{x}=[x_1,x_2, x_3, x_4]^T x=[x1​,x2​,x3​,x4​]T

f 1 ( x ) = x 1 + 10 x 2 f 2 ( x ) = 5 ( x 3 − x 4 ) f 3 ( x ) = ( x 2 − 2 x 3 ) 2 f 4 ( x ) = 10 ( x 1 − x 4 ) 2 F ( x ) = [ f 1 ( x ) , f 2 ( x ) , f 3 ( x ) , f 4 ( x ) ] \begin{aligned}f_1(\boldsymbol{x})&=x_1 + 10x_2 \\ f_2(\boldsymbol{x})&=\sqrt{5}(x_3 -x_4) \\ f_3(\boldsymbol{x})&=(x_2 -2x_3)^2 \\ f_4(\boldsymbol{x})&=\sqrt{10}(x_1 -x_4)^2 \\ F(\boldsymbol{x}) &= [f_1(\boldsymbol{x}), f_2(\boldsymbol{x}), f_3(\boldsymbol{x}), f_4(\boldsymbol{x})] \end{aligned} f1​(x)f2​(x)f3​(x)f4​(x)F(x)​=x1​+10x2​=5 ​(x3​−x4​)=(x2​−2x3​)2=10 ​(x1​−x4​)2=[f1​(x),f2​(x),f3​(x),f4​(x)]​

首先构造四个仿函数

struct F1 {
  template <typename T>
  bool operator()(const T* const x1, const T* const x2, T* residual) const {
    // f1 = x1 + 10 * x2;
    residual[0] = x1[0] + 10.0 * x2[0];
    return true;
  }
};
struct F2 {
  template <typename T>
  bool operator()(const T* const x3, const T* const x4, T* residual) const {
    // f2 = sqrt(5) (x3 - x4)
    residual[0] = sqrt(5.0) * (x3[0] - x4[0]);
    return true;
  }
};
struct F3 {
  template <typename T>
  bool operator()(const T* const x2, const T* const x3, T* residual) const {
    // f3 = (x2 - 2 x3)^2
    residual[0] = (x2[0] - 2.0 * x3[0]) * (x2[0] - 2.0 * x3[0]);
    return true;
  }
};
struct F4 {
  template <typename T>
  bool operator()(const T* const x1, const T* const x4, T* residual) const {
    // f4 = sqrt(10) (x1 - x4)^2
    residual[0] = sqrt(10.0) * (x1[0] - x4[0]) * (x1[0] - x4[0]);
    return true;
  }
};

接着构建最小二乘问题

double x1 = 3.0;
double x2 = -1.0;
double x3 = 0.0;
double x4 = 1.0;
ceres::Problem problem;
problem.AddResidualBlock(
    new ceres::AutoDiffCostFunction<F1, 1, 1, 1>(new F1), nullptr, &x1, &x2);
problem.AddResidualBlock(
    new ceres::AutoDiffCostFunction<F2, 1, 1, 1>(new F2), nullptr, &x3, &x4);
problem.AddResidualBlock(
    new ceres::AutoDiffCostFunction<F3, 1, 1, 1>(new F3), nullptr, &x2, &x3);
problem.AddResidualBlock(
    new ceres::AutoDiffCostFunction<F4, 1, 1, 1>(new F4), nullptr, &x1, &x4);

最后优化求解

ceres::Solver::Options options;
options.max_num_iterations = 100;
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = false;
// clang-format off
std::cout << "Initial x1 = " << x1
          << ", x2 = " << x2
          << ", x3 = " << x3
          << ", x4 = " << x4
          << "\n";
// clang-format on
// Run the solver!
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
// std::cout << summary.FullReport() << "\n";
// clang-format off
std::cout << "Final x1 = " << x1
          << ", x2 = " << x2
          << ", x3 = " << x3
          << ", x4 = " << x4
          << "\n";
// clang-format on
return 0;

输出结果

Initial x1 = 3, x2 = -1, x3 = 0, x4 = 1
Final x1 = 0.000146222, x2 = -1.46222e-05, x3 = 2.40957e-05, x4 = 2.40957e-05

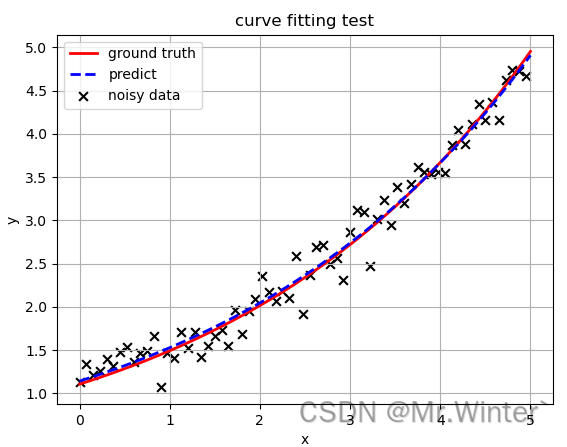
4.2 非线性曲线拟合

考虑如下方程：
y = e m x + c + w y=e^{m{x}+c}+\boldsymbol{w} y=emx+c+w
其中 m m m、 c c c是待估计的曲线参数， w w w是高斯噪声，假设有 n n n个观测样本 ( x i , y i ) (x_i,y_i) (xi​,yi​)，希望根据这组样本得到最佳的曲线参数，构造如下的优化问题

F ( θ ) = min ⁡ 1 2 n ∑ i = 1 n ( y i − e m x i 2 + c ) 2 F(\boldsymbol{\theta})=\min \frac{1}{2n}\sum_{i=1}^{n}{(y_i-e^{mx_i^2+c})^2} F(θ)=min2n1​i=1∑n​(yi​−emxi2​+c)2

struct ExponentialResidual
{
  ExponentialResidual(double x, double y) : x_(x), y_(y)
  {
  }
  template <typename T>
  bool operator()(const T* const params, T* residual) const
  {
    residual[0] = y_ - exp(params[0] * x_ + params[1]);
    return true;
  }

private:
  const double x_;
  const double y_;
};

int main(int argc, char** argv)
{
  std::vector<double> pt_x, pt_y, ground_truth_x, ground_truth_y, predict_x, predict_y;
  const double initial_m = 0.0;
  const double initial_c = 0.0;
  std::vector<double> params(2);
  ceres::Problem problem;
  for (int i = 0; i < kNumObservations; ++i)
  {
    pt_x.push_back(data[2 * i]);
    pt_y.push_back(data[2 * i + 1]);
    problem.AddResidualBlock(new ceres::AutoDiffCostFunction<ExponentialResidual, 1, 2>(
                                 new ExponentialResidual(data[2 * i], data[2 * i + 1])),
                             nullptr, params.data());
  }
  ceres::Solver::Options options;
  options.max_num_iterations = 25;
  options.linear_solver_type = ceres::DENSE_QR;
  options.minimizer_progress_to_stdout = false;
  ceres::Solver::Summary summary;
  ceres::Solve(options, &problem, &summary);
  std::cout << "Initial m: " << initial_m << " c: " << initial_c << "\n";
  std::cout << "Final   m: " << params[0] << " c: " << params[1] << "\n";

  double dx = 0.1, x = 0.0;
  while (x < 5.0)
  {
    ground_truth_x.push_back(x);
    ground_truth_y.push_back(std::exp(0.3 * x + 0.1));
    predict_x.push_back(x);
    predict_y.push_back(std::exp(params[0] * x + params[1]));
    x += dx;
  }
  plt::plot(ground_truth_x, ground_truth_y,
            { { "color", "r" }, { "linewidth", "2.0" }, { "linestyle", "-" }, { "label", "ground truth" } });
  plt::plot(predict_x, predict_y,
            { { "color", "b" }, { "linewidth", "2.0" }, { "linestyle", "--" }, { "label", "predict" } });
  plt::scatter(pt_x, pt_y, 40, { { "color", "k" }, { "marker", "x" }, { "label", "noisy data" } });
  plt::xlabel("x");
  plt::ylabel("y");
  plt::title("curve fitting test");
  plt::legend();
  plt::grid(true);
  plt::show();
  return 0;
}

在这里插入图片描述

完整工程代码请联系下方博主名片获取

🔥 更多精彩专栏：

  • 《ROS从入门到精通》
  • 《Pytorch深度学习实战》
  • 《机器学习强基计划》
  • 《运动规划实战精讲》
  • …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2247646.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Flink Transformation-转换算子

Flink Transformation-转换算子

map算子的使用 假如有如下数据&#xff1a; 86.149.9.216 10001 17/05/2015:10:05:30 GET /presentations/logstash-monitorama-2013/images/github-contributions.png 83.149.9.216 10002 17/05/2015:10:06:53 GET /presentations/logstash-monitorama-2013/css/print/paper…
阅读更多...
记录一些PostgreSQL操作

记录一些PostgreSQL操作

本文分享一些pg操作 查看版本 select version(); PostgreSQL 11.11 查看安装的插件 select * from pg_available_extensions; 查看分词效果 select ‘我爱北京天安门,天安门上太阳升’::tsvector; ‘天安门上太阳升’:2 ‘我爱北京天安门’:1select to_tsvector(‘我爱北京天…
阅读更多...
【ubuntu】数学人的环境搭建

【ubuntu】数学人的环境搭建

Python 语言环境 python 的 pip 第三方库管理 sudo apt install python3-pippython 的 idle 界面 sudo apt install idle3R 语言环境 sudo apt install r-cran-zoo### RStudio 界面 ubuntu sudo snap install rstudio --classicJulia 语言环境 sudo snap install julia --…
阅读更多...
android 11添加切换分屏功能

android 11添加切换分屏功能

引言 自Android 7开始官方就支持分屏显示，但没有切换分屏的功能，即交换上下屏幕。直到Android 13开始才支持切换分屏，操作方式是：分屏模式下双击中间分割线就会交换上下屏位置。本文的目的就是在Android 11上实现切换分屏的功能。 下图是Android13切换分屏演示 切换分屏…
阅读更多...
数据结构——排序算法第一幕（插入排序：直接插入排序、希尔排序 选择排序：直接选择排序，堆排序）超详细！！！！

数据结构——排序算法第一幕（插入排序：直接插入排序、希尔排序 选择排序：直接选择排序，堆排序）超详细！！！！

文章目录 前言一、排序1.1 概念1.2 常见的排序算法 二、插入排序2.1 直接插入排序2.2 希尔排序希尔排序的时间复杂度 三、选择排序3.1 直接选择排序3.2 堆排序 总结 前言 时间很快&#xff0c;转眼间已经到数据结构的排序算法部分啦 今天我们来学习排序算法当中的 插入排序 和 …
阅读更多...
C++网络编程之多播

C++网络编程之多播

概述 在移动互联网时代&#xff0c;随着多媒体应用的日益普及&#xff0c;如何高效地将数据传输给多个接收者成为了网络通信领域的一个重要课题。多播&#xff08;英文为Multicast&#xff09;作为一种高效的网络通信方式&#xff0c;可以将数据同时发送到多个接收者&#xff0…
阅读更多...
AWS的流日志

AWS的流日志

文章目录 一、aws如何观察vpc的日志&#xff1f;二、aws观测其vpc的入口日志三、 具体配置3.1、配置你的存储神器 S33.2、建立子网的流日志 一、aws如何观察vpc的日志&#xff1f; 排查问题的时候除了去抓包看具体的端口信息的时候&#xff0c;还可以根据其所在的vpc的子网信息…
阅读更多...
C++ —— 以真我之名 如飞花般绚丽 - 智能指针

C++ —— 以真我之名 如飞花般绚丽 - 智能指针

目录 1. RAII和智能指针的设计思路 2. C标准库智能指针的使用 2.1 auto_ptr 2.2 unique_ptr 2.3 简单模拟实现auto_ptr和unique_ptr的核心功能 2.4 shared_ptr 2.4.1 make_shared 2.5 weak_ptr 2.6 shared_ptr的缺陷&#xff1a;循环引用问题 3. shared_ptr 和 unique_…
阅读更多...
DAMODEL丹摩｜《ChatGLM-6B 在丹摩智算平台的部署与使用指南》

DAMODEL丹摩｜《ChatGLM-6B 在丹摩智算平台的部署与使用指南》

目录 一、引言 二、ChatGLM-6B 模型简介 ChatGLM-6B 的特点 三、DAMODEL 平台部署 ChatGLM-6B 1. 实例创建 2. 模型准备 3. 模型启动 四、通过 Web API 实现本地使用 1. 启动服务 2. 开放端口 3. 使用 PostMan 测试功能 4. 本地代码使用功能 五、总结 一、引言 Ch…
阅读更多...
【AI大模型】LLM的检索增强--SELF-RAG

【AI大模型】LLM的检索增强--SELF-RAG

本篇博客参考论文&#xff1a; 《SELF-RAG: LEARNING TO RETRIEVE, GENERATE, AND CRITIQUE THROUGH SELF-REFLECTION》 在自然语言处理&#xff08;NLP&#xff09;领域&#xff0c;大型语言模型&#xff08;LLMs&#xff09;已成为处理复杂语言任务的强大工具。然而&#xf…
阅读更多...
Linux—进程概念学习-03

Linux—进程概念学习-03

目录 Linux—进程学习—31.进程优先级1.1Linux中的进程优先级1.2修改进程优先级—top 2.进程的其他概念3.进程切换4.环境变量4.0环境变量的理解4.1环境变量的基本概念4.2添加环境变量—export4.3Linux中环境变量的由来4.4常见环境变量4.5和环境变量相关的命令4.6通过系统调用获…
阅读更多...
C# 读取多条数据记录导出到 Word标签模板之图片输出改造

C# 读取多条数据记录导出到 Word标签模板之图片输出改造

目录 应用需求 设计 范例运行环境 配置Office DCOM 实现代码 组件库引入 ​核心代码 调用示例 小结 应用需求 在我的文章《C# 读取多条数据记录导出到 Word 标签模板》里&#xff0c;讲述读取多条数据记录结合 WORD 标签模板输出文件的功能&#xff0c;原有输出图片的…
阅读更多...
Android 性能优化：内存优化（理论篇）

Android 性能优化：内存优化（理论篇）

内存作为App程序运行最重要的资源之一&#xff0c;需要运行过程中做到合理的资源分配与回收&#xff0c;不合理的内存占用轻则使得用户应用程序运行卡顿、ANR、黑屏&#xff0c;重则导致用户应用程序发生 OOM&#xff08;out of memory&#xff09;崩溃。喜马直播随着近些年的业…
阅读更多...
【AI技术赋能有限元分析应用实践】pycharm终端与界面设置导入Abaqus2024自带python开发环境

【AI技术赋能有限元分析应用实践】pycharm终端与界面设置导入Abaqus2024自带python开发环境

目录 一、具体说明1. **如何在 Windows 环境中执行 Abaqus Python 脚本**2. **如何在 PyCharm 中配置并激活 Abaqus Python 环境**3. **创建 Windows 批处理脚本自动执行 Abaqus Python 脚本**总结二、方法1：通过下面输出获取安装路径导入pycharm方法2：终端脚本执行批处理脚本…
阅读更多...
arm学习总结

arm学习总结

AHB总线连接的都是这些需要高速处理的内存、内核啥的 APB连接的都是些外设 GPIO并不需要高速处理的
阅读更多...
【redis 】string类型详解

【redis 】string类型详解

string类型详解 一、string类型的概念二、string类型的常用指令2.1 SET2.2 GET2.3 MSET2.4 MGET2.5 SETNX2.6 INCR2.7 INCRBY2.8 DECR2.9 DECRBY2.10 INCRBYFLOAT2.11 APPEND2.12 GETRANGE2.13 SETRANGE2.14 STRLEN 三、string类型的命令小结四、string类型的内部编码五、strin…
阅读更多...
Mysql案例之COALESCE函数使用详解

Mysql案例之COALESCE函数使用详解

hello&#xff0c;大家好&#xff0c;我是灰小猿&#xff01;最近在做一个三表关联查询的场景处理时&#xff0c;遇到了一个比较有用的MySQL函数&#xff0c;在这里记录一下&#xff0c;大概场景如下&#xff1a; 需求场景 场景&#xff1a;有一张object_rel表&#xff0c;表中…
阅读更多...
C语言菜鸟入门·关键字·int的用法

C语言菜鸟入门·关键字·int的用法

目录 1. int关键字 1.1 取值范围 1.2 符号类型 1.3 运算 1.3.1 加法运算() 1.3.2 减法运算(-) 1.3.3 乘法运算(*) 1.3.4 除法运算(/) 1.3.5 取余运算(%) 1.3.6 自增()与自减(--) 1.3.7 位运算 2. 更多关键字 1. int关键字 int 是一个关键字&#xff0…
阅读更多...
D74【 python 接口自动化学习】- python 基础之HTTP

D74【 python 接口自动化学习】- python 基础之HTTP

day74 http基础定义 学习日期&#xff1a;20241120 学习目标&#xff1a;http定义及实战 -- http基础介绍 学习笔记&#xff1a; HTTP定义 HTTP 是一个协议&#xff08;服务器传输超文本到浏览器的传送协议&#xff09;&#xff0c;是基于 TCP/IP 通信协议来传递数据&…
阅读更多...
基于FPGA（现场可编程门阵列）的SD NAND图片显示系统是一个复杂的项目，它涉及硬件设计、FPGA编程、SD卡接口、NAND闪存控制以及图像显示等多个方面

基于FPGA（现场可编程门阵列）的SD NAND图片显示系统是一个复杂的项目，它涉及硬件设计、FPGA编程、SD卡接口、NAND闪存控制以及图像显示等多个方面

文章目录 0、前言 1、目标 2、图片的预处理 3、SD NAND的预处理 4、FPGA实现 4.1、详细设计 4.2、仿真 4.3、实验结果 前言 在上一篇文章《基于FPGA的SD卡的数据读写实现&#xff08;SD NAND FLASH&#xff09;》中&#xff0c;我们了解到了SD NAND Flash的相关知识&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023