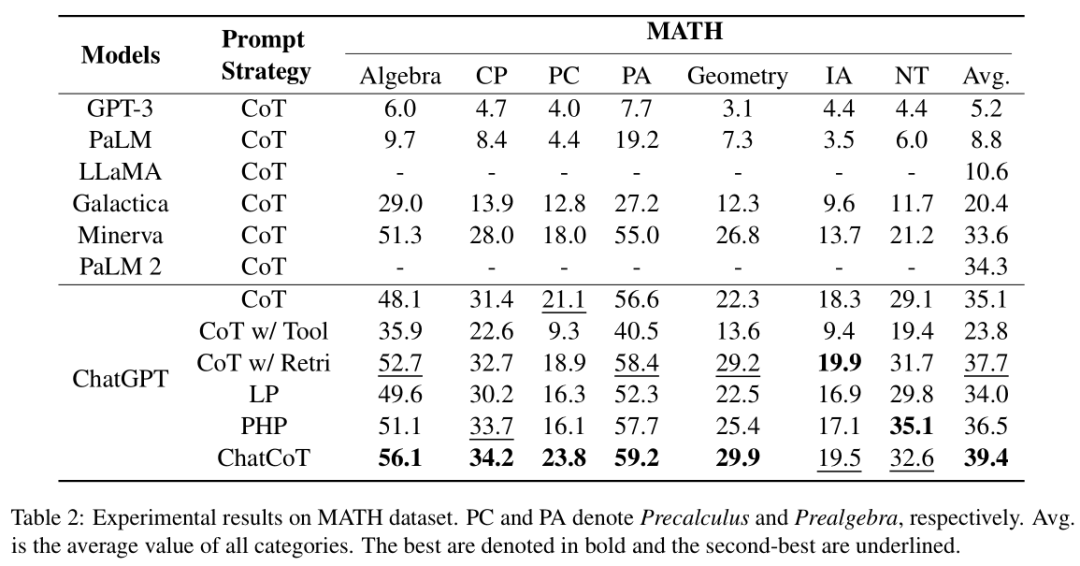
学习曲线是帮助理解学习算法如何工作的一种方法,作为它所拥有的经验的函数。
绘制一个符合二阶模型的学习曲线,多项式或二次函数,画出交叉验证错误Jcv,以及Jtrain训练错误,所以在这个曲线中,横轴将是Mtrain,即训练集大小或算法可以从中学习的示例数,在垂直轴上,画出误差,所以让我们从绘制交叉验证错误开始,绿线代表Jcv(w,b),当Jtrain训练集规模变大,所以交叉验证错误现在下降了,绘制训练错误的Jtrain(w,b),随着训练集的规模越来越大,原来训练错误实际上会是这样的(蓝线),随着训练集的规模越来越大,训练集误差实际上增大了,为什么会出现这种情况?
将从一个例子开始,当你只有一个训练例子,如果你拟合一个二次模型,你可以很容易的知道直线或曲线,你的训练误差将为0,如果你有两个这样的训练例子,你可以再次拟合一条直线,实现零训练误差,事实上,如果你有三个训练例子,二次函数仍可以很好的拟合这一点,几乎没有训练错误,但是如果你的训练集再大一点,假设你有四个训练例子,然后要完美地适应所有四个例子就变得有点难了,你可能会得到一条曲线,看起来很适合它,所以当你把训练集的大小增加到四个,训练误差实际上上升了一点,我们有五个训练例子怎么样你可以更好的适应它?但是要完全适应它们就更难了,当你有一个更大的训练集,只是越来越难适应每一个你的训练例子,所以总结一下,当你有非常少的训练例子,像一两个甚至三个,相对容易得到零或非常小的训练误差,但是当你有一个更大的训练集,对于二次函数来说更难完美地拟合所有的训练示例,这就是为什么随着训练集变得越来越大,训练误差增加是因为很难拟合所有的训练示例,注意这些曲线的另一个特点,交叉验证误差通常会高于训练误差,因为你将参数拟合到训练集,或者当m小的时候,也许在训练集上比在交叉验证集上要好得多。

现在让我们看看学习曲线是什么样的?
对于高偏差算法和高方差算法,让我们从高偏差或不合身的情况开始,回想一下,高偏差的一个例子是如果你把一个线性函数拟合到一条曲线上,,如果你要绘制训练错误,然后训练误差会像你预期的那样上升,事实上,这条训练误差曲线可能会开始变平,或者称之为高原,意思是过了一段时间就变平了,这是因为当你得到越来越多的训练例子,当你拟合简单的线性函数时,你的模型实际上变化不大,它符合一条直线,即使你得到越来越多的例子,没有太多要改变的了,这就是为什么平均训练误差在那时间后就会变平,同样,交叉验证出错误也会下降,一段时间也会变平,这就是为什么Jcv又比Jtrain高,但Jcv往往看起来像那样,因为超过了某一点,即使你得到越来越多的例子,拟合的直线不会有太大的变化,这只是一个太简单的模型,不适用于这么多数据,所以这两条曲线,Jcv和Jtrain趋于平坦,如果你有一个基准性能水平的衡量标准,例如人的水平表现,然后它将倾向于一个低于Jtrain的值,还有Jcv,所以人类水平的表现可能是这样的。在性能的基线水平和Jtrain之间有很大的差距,我们发现这个算法有很高的偏差。

如果你能有一个更大的训练集,如果把m值增加到比这张图的右边更远的地方,会是什么样子?
想象如果把这两条曲线都向右延伸,它们都变平了,它们两个可能会继续像那样扁平,无论向右边延伸多远,这条曲线永远不会相交,找到一种方法来降低人类的表演水平,或者一直像这样扁平下去,不管训练集有多大,如果一个算法有很高的偏差,获取更多的训练数据本身并没有多大的帮助,我们习惯于认为有更多的数据是好的,但是如果算法有很高的偏差,那么唯一做的就是向它扔更多的训练数据,它本身不会让你降低那么多的错误率,无论在这个图中添加多少示例,直线拟合不会变的更好,这就是为什么再投入大量精力收集更多训练数据之前值得检查学习算法是否有很高的偏差。

现在让我们看看学习曲线是什么样子的?
对于一种高方差的学习算法,如果你拟合一个四阶多项式,对于小的lambda甚至lambda=0,得到一个曲线,如右上图所示,即使它很符合训练数据,它不能概括,在这种高方差的情况下,随着训练集模型的增加,Jtrain将上升,Jcv会更高,所以你的交叉验证错误比你的训练错误高得多,事实上,这里有一个巨大的差距,高方差在训练集上做得更好,比在交叉集上做得要多,如果你要绘制性能的基线水平,例如人的表现水平,Jtrain有时甚至比人类的性能水平还要低,也可能人类水平的表现比这低一点,但是当你过度训练的时候,也许能很好的适应训练集,有一个不切实际的低误差,比如这个例子中的零误差。人类实际上能够预测房价,或者正在处理应用的程序,高方差的信号是Jcv是否远高于Jtrain,当你有很高的方差时,那么增加训练集的大小可能会有很大的帮助,特别是如果我们能把这些曲线外推到合适的增量Mtrain上,训练误差还会继续往上走,但是交叉验证错误有希望下降并接近Jtrain,所以在这种情况下,仅仅通过增加训练集的大小来降低交叉验证错误是可能的,为了让你的算法性能越来越好,这与高偏差情况不同,如果你唯一要做的是得到更多的训练数据,这实际上不会帮助您的学习算法的性能,总而言之,如果学习算法存在高方差,那么获得更多训练的数据确实可能有所帮助。在这个例子中,只需获取更多训练数据,允许算法从这个相对较高的交叉验证错误更接近人类水平的表现。如果你增加更多的训练例子,并继续拟合四阶多项式,就会得到一个更好的四阶多项式拟合这个数据。

因此,如果你正在构建一个机器学习应用程序,你可以画出学习曲线,可以将训练集的不同子集,即使有一千个训练例子,可以用一百个训练例子来训练一个模型,看看训练错误和交叉验证错误,然后再两百个例子上训练一个模型,重复并绘制出学习曲线是什么样子,如果你的学习曲线看起来更像是高偏差或高方差,使用训练集的不同大小的子集。