LeetCode 力扣热题 100道（五）最长回文子串（C++）

news2024/11/19 5:45:14

最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

回文性
如果字符串向前和向后读都相同，则它满足 回文性
子字符串
子字符串 是字符串中连续的非空字符序列。

动态规划法

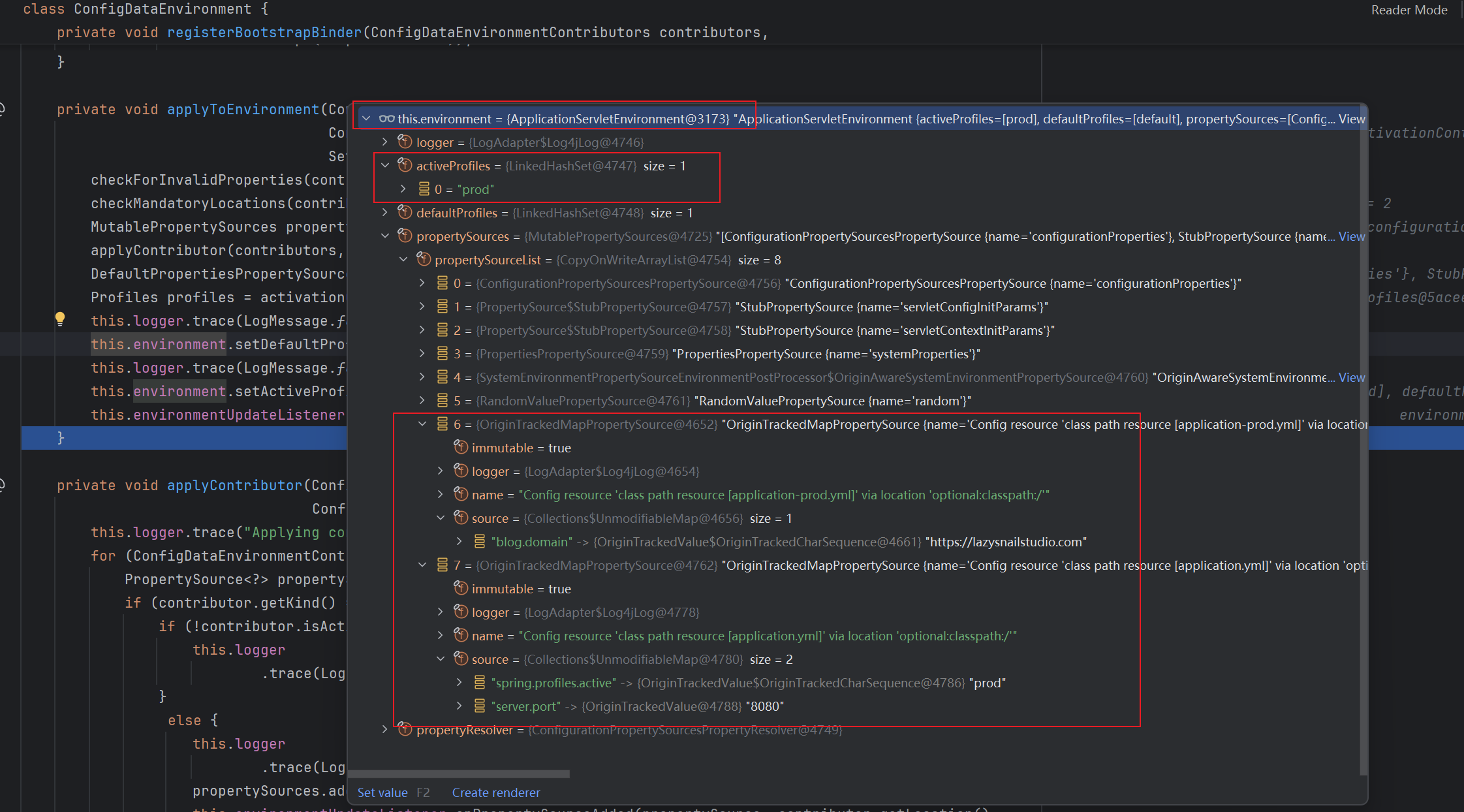
class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        if (n <= 1) return s;

        vector<vector<bool>> dp(n, vector<bool>(n, false));
        int start = 0, maxLen = 1;

        for (int i = 0; i < n; ++i) dp[i][i] = true;
        for (int i = 0; i < n - 1; ++i) {
            if (s[i] == s[i + 1]) {
                dp[i][i + 1] = true;
                start = i;
                maxLen = 2;
            }
        }

        for (int len = 3; len <= n; ++len) {
            for (int i = 0; i + len - 1 < n; ++i) {
                int j = i + len - 1;
                if (s[i] == s[j] && dp[i + 1][j - 1]) {
                    dp[i][j] = true;
                    start = i;
                    maxLen = len;
                }
            }
        }

        return s.substr(start, maxLen);
    }
};

首先，我们获取字符串 s 的长度 n。如果字符串长度小于或等于 1，则字符串本身就是回文的（单个字符本身就是回文），直接返回字符串。

dp 是一个二维布尔型数组，dp[i][j] 用来表示子串 s[i...j] 是否为回文串。数组大小为 n x n，初始化为 false。

每个单字符子串（即 s[i...i]）自然是回文的，因此将 dp[i][i] 设置为 true。

接下来，我们处理长度为 2 的子串。如果 s[i] == s[i+1]，那么 s[i...i+1] 是回文串，设置 dp[i][i+1] = true。此时，我们还更新 start 和 maxLen，记录最长回文子串的起始位置和长度。

从长度为 3 的子串开始，我们逐步扩展到更长的回文子串。具体来说，len 表示当前子串的长度，从 3 一直增加到 n。

对于每个长度为 len 的子串，我们通过以下条件判断是否为回文：

s[i] == s[j]：当前子串的首尾字符相同。
dp[i+1][j-1]：即子串 s[i+1...j-1] 是否是回文。

如果这两个条件都成立，那么 s[i...j] 也是回文子串，更新 dp[i][j] = true，并更新 start 和 maxLen，记录当前最长回文子串的起始位置和长度。

输入字符串 s = "babad"：

长度为 1 的子串：我们从一开始就知道每个单独的字符都是一个回文子串，所以 dp[i][i] = true 对于所有 i 都成立。对于 s = "babad"，初始化时，dp 数组是这样的：

dp = [ [true, false, false, false, false], [false, true, false, false, false], [false, false, true, false, false], [false, false, false, true, false], [false, false, false, false, true] ]

长度为 2 的子串：接着，代码检查相邻的字符是否相同。如果相同，设置 dp[i][i+1] = true。在 s = "babad" 中，s[0] != s[1]（b != a），s[1] != s[2]（a != b），s[2] != s[3]（b != a），s[3] != s[4]（a != d）。所以 dp 数组没有更新。

dp 仍然是：

dp = [ [true, false, false, false, false], [false, true, false, false, false], [false, false, true, false, false], [false, false, false, true, false], [false, false, false, false, true] ]

长度为 3 及以上的回文子串：接着，程序检查长度为 3 及以上的子串，逐步扩展回文子串的长度。对每一个 len（长度从 3 到 n），我们依次检查每个子串的起始位置 i。
- 当 len = 3 时：
  - 对于 s[0...2] = "bab"，s[0] == s[2]（b == b），并且 dp[1][1] = true（即 "a" 是回文）。所以 dp[0][2] = true，start = 0，maxLen = 3。
  - 现在 dp 数组更新为：
  dp = [ [true, false, true, false, false], [false, true, false, false, false], [false, false, true, false, false], [false, false, false, true, false], [false, false, false, false, true] ]
  
  这时，我们已经找到了 "bab" 作为一个回文子串。
继续检查更长的回文子串：
- 当 len = 4 时：
  - 对于 s[1...4] = "abad"，s[1] != s[4]（a != d），所以 dp[1][4] 不会被设置。
- 当 len = 5 时：
  - 对于 s[0...4] = "babad"，s[0] != s[4]（b != d），所以 dp[0][4] 也不会被设置。