消息鉴别的缺陷

消息鉴别保证了数据完整性，消息不被第三方侵犯，但是不保证双方之间的欺骗。如果A发送认证消息给B，可能会存在多种争议：
B伪造一个不同的消息，声称是A发的
A否认发过这个消息，B无法证明A确实发了消息。

比如股票交易亏损的抵赖等等。

数字签名

签名者无法否认。
接受者可以校验签名，任何其他人无法伪造签名。
有争议时第三方可验证。
对签名的作者，日期和时间提供验证。

因此签名提供了有别于鉴定的功能，抗抵赖。

签名方案的攻击模型

唯秘钥攻击：攻击者有公钥，即验证函数
已知消息攻击：攻击者有A过去签名的一系列消息和签名
选择消息攻击：攻击者可以要求A对一系列消息签名

签名方案的攻击目的

完全破译：攻击者掌握了私钥，可以任意制造A的签名
选择性伪造：攻击者有一定概率可以对另一个消息做出有效签名。
存在性伪造：攻击者至少能为一个A未签名过的消息做出有效签名。

数字签名设计

1.依赖被签名信息
2.依赖某些对发送者唯一的信息，以抗抵赖
3.相对容易生成
4.相对容易验证和识别
5.伪造签名计算不可行，包括根据签名伪造信息，或根据信息伪造签名
6.存储器中存储一个签名是可行的

数字签名分类

验证方式分类：直接数字签名，仲裁数字签名
计算能力分类：无条件安全，计算上安全
可签名次数分类：一次性，多次性
其他特殊性质

直接数字签名

签名依赖发送者的密钥，发送者要抵赖时可以宣称自己的私钥丢失或者失窃，从而被他人伪造签名。
改进:将已暴露的私钥交给授权中心，行政手段…

仲裁数字签名

引入仲裁者，所有签名信息交由仲裁者测试，关键在于仲裁者。参与者必须信任仲裁者系统的正常工作。

签名和加密

签名提供真实性，加密提供保密性。
可以先签名后加密
先加密后签名的方式存在安全隐患，容易导致已知明文攻击。

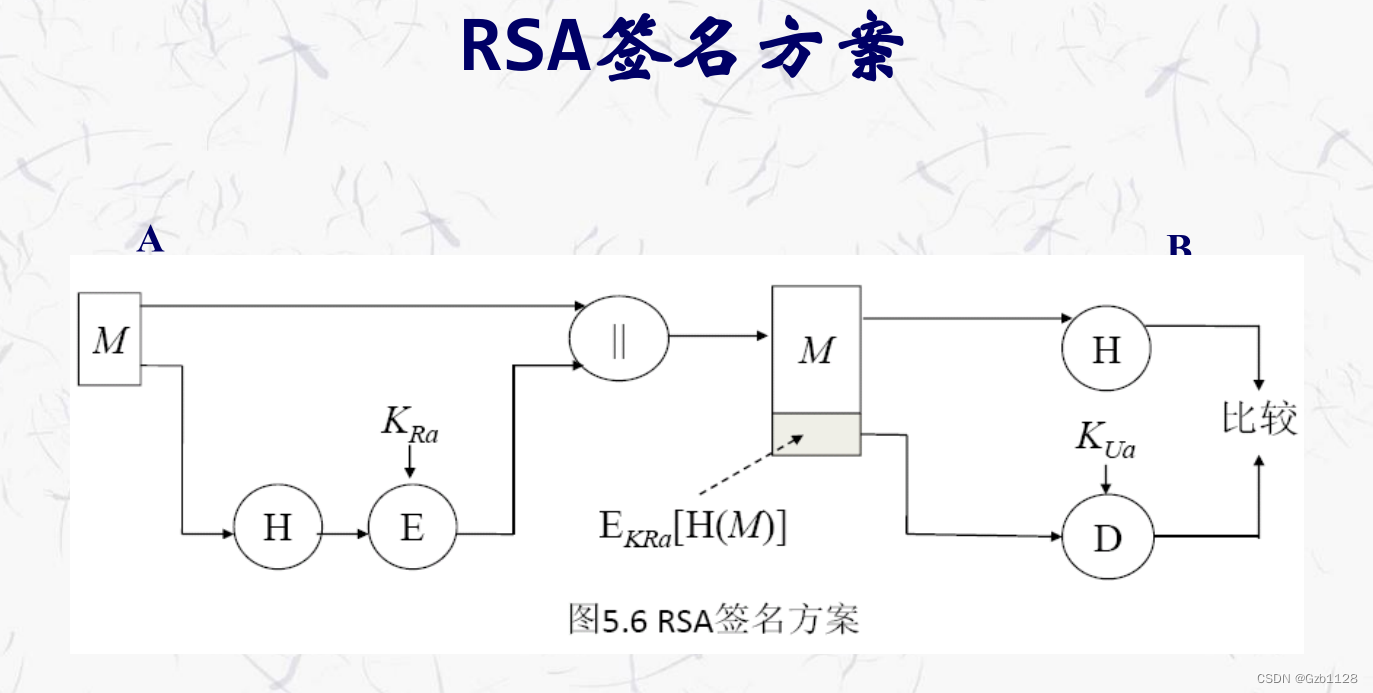
RSA签名

schnorr数字签名

基于离散对数
全局公钥{p,q,a}
p是素数，1024位整数，q是(p-1)的素因子，160位，选择a使得$a^q\equiv 1modp$
用户私钥{s}
s是随机整数,0<s<q
用户公钥{v}
$v=a^{-s}modp$

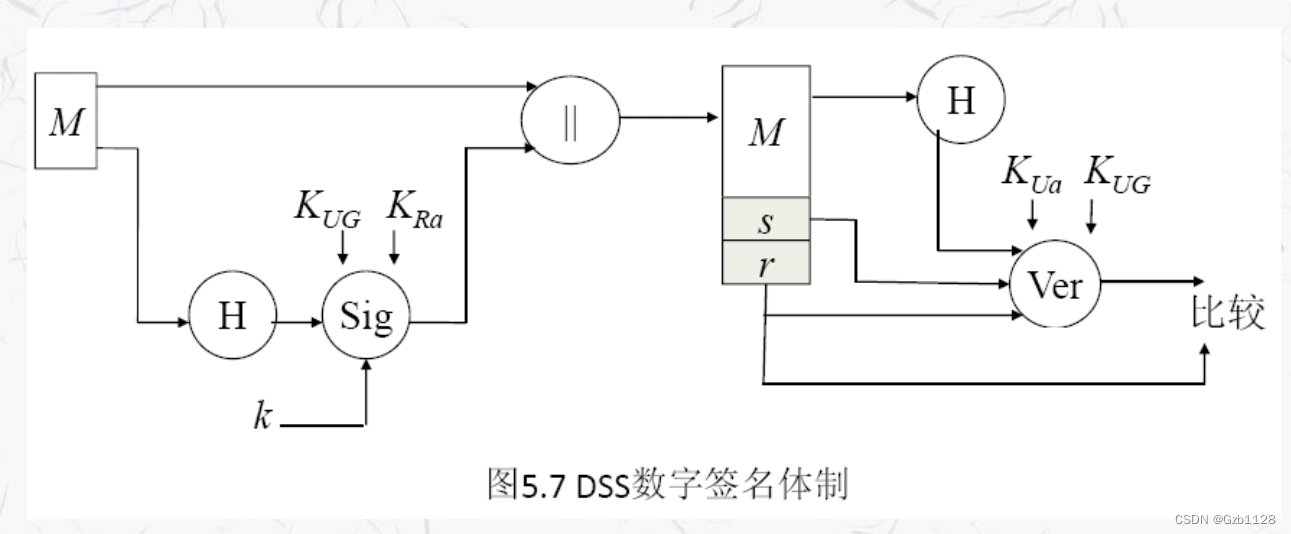
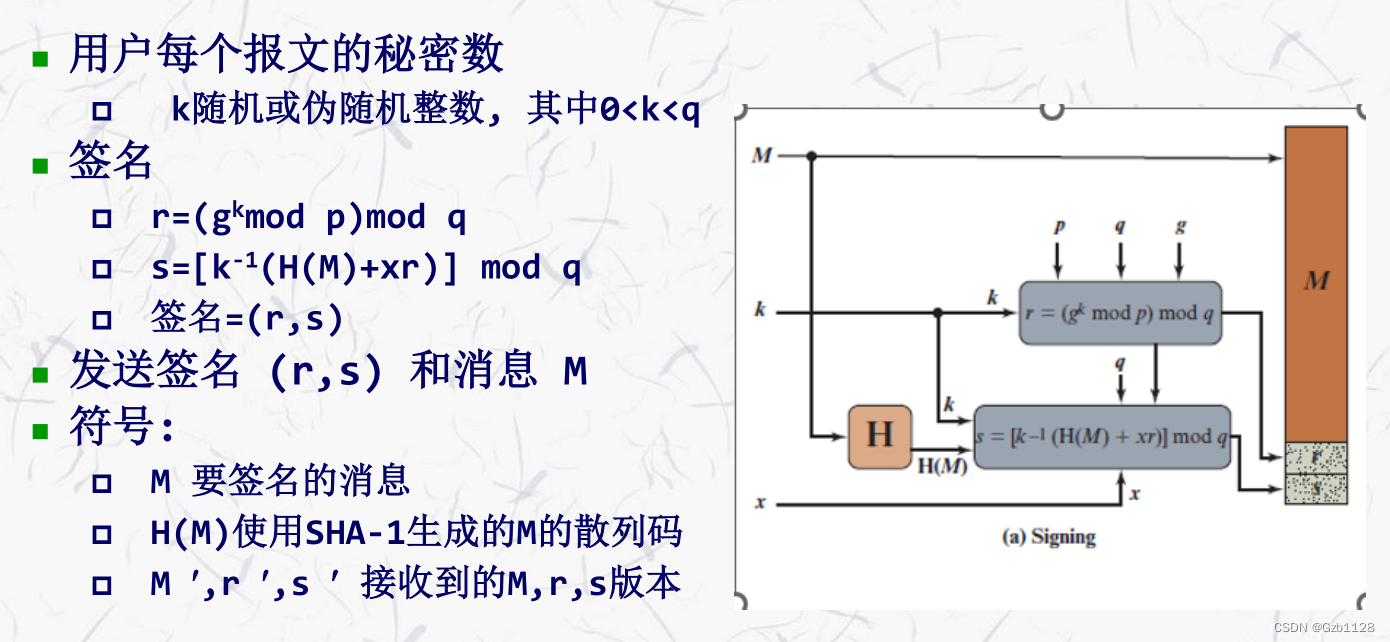
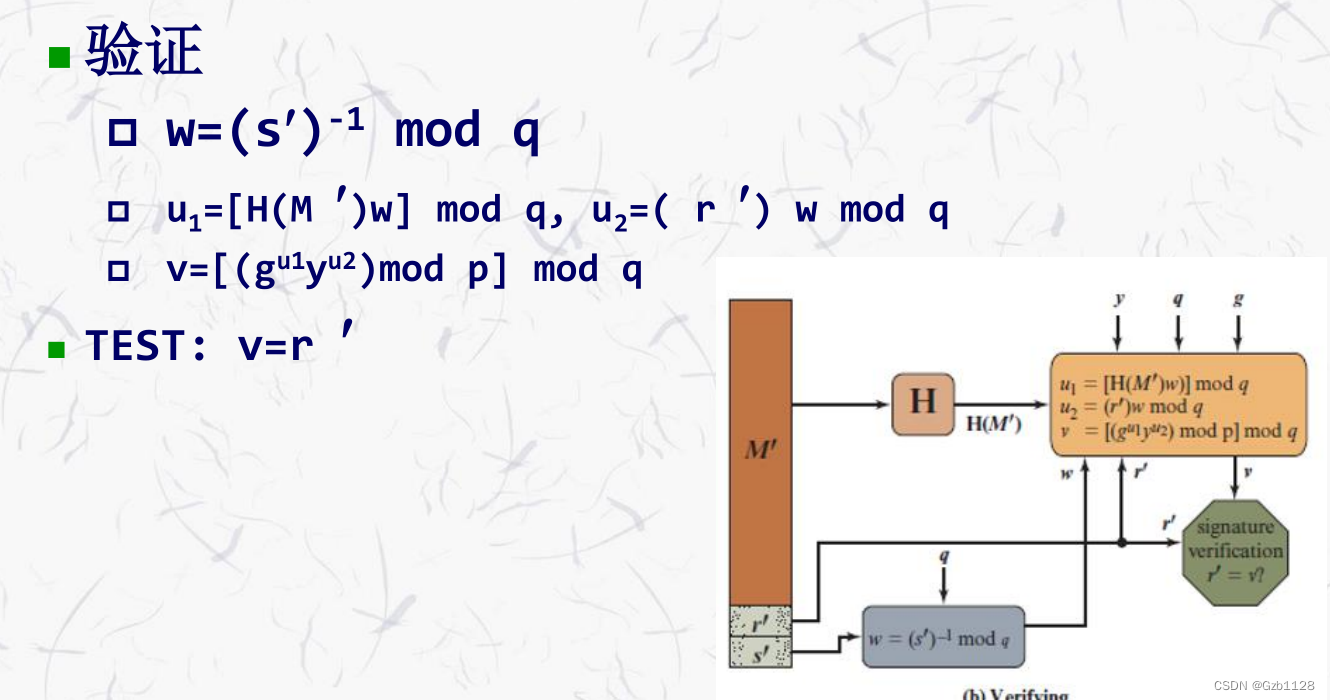
DSS签名方案