【机器学习】决定系数（R²：Coefficient of Determination）

news2024/11/14 11:54:23

决定系数 $R^{2}$ ，也称为 R 平方，是一种用于衡量回归模型预测效果的统计指标。它表示了模型解释目标变量总变异的程度，数值介于 0 和 1 之间，数值越接近 1 表明模型的解释力越强。

1. 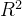$R^{2}$ 的定义和公式

$R^{2}$ 的公式如下：

$R^2 = 1 - \frac{\sum_{i=1}^n (y_i - \hat{y}_i)^2}{\sum_{i=1}^n (y_i - \bar{y})^2}$

其中：

$y_{i}$ 是真实值。
$\hat{y_{i}}$ 是模型的预测值。
$\bar{y}$ 是真实值的平均值。
$\sum_{i=1}^n (y_i - \hat{y}_i)^2$ 是残差平方和 (Residual Sum of Squares, RSS)。
$\sum_{i=1}^n (y_i - \bar{y})^2$ 是总平方和 (Total Sum of Squares, TSS)。

从公式可以看出， $R^2$ 表示残差平方和占总平方和的比例。换句话说， $R^2$ 越接近 1，表示模型的预测越接近真实值，模型解释越充分。

2. 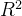$R^2$ 的计算步骤

计算 $R^2$ 的步骤如下：

计算真实值的平均值 $\bar{y}$ 。
计算残差平方和 $\sum (y_i - \hat{y}_i)^2$ 。
计算总平方和 $\sum (y_i - \bar{y})^2$ 。
计算 $R^2$ 值，即使用公式 $R^2 = 1 - \frac{\text{RSS}}{\text{TSS}}$ 。

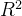3. $R^2$ 的解释和意义

解释度： $R^2$ 值表示自变量解释因变量变异的比例。例如， $R^2 = 0.8$ 表示模型能解释 80% 的目标变量变异。
值域： $R^2$ 的取值范围通常为 [0, 1]。0 表示模型无法解释任何目标变量的变异，1 表示模型可以完全解释目标变量的变异。
负值的情况：在某些情况下，当模型预测效果极差时（例如，模型欠拟合）， $R^2$ 可能为负数。这表示预测值甚至比用平均值预测的效果更差。

4. 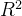$R^2$ 的优缺点

优点

直观解释： $R^2$ 直接表示了模型对目标变量的解释力。
适用性广：广泛应用于回归模型的效果评价。

缺点

对样本大小敏感：在小样本数据中， $R^2$ 值容易偏高，可能夸大模型的预测效果。
对异常值敏感：由于平方的存在， $R^2$ 对异常值敏感，异常值可能会过度影响结果。
无法区分方向性：仅仅反映解释力，不反映模型预测的方向性，容易掩盖预测偏差。

5. 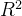$R^2$ 的应用

在回归分析、机器学习和经济学等领域， $R^2$ 是一种常用的评价指标。其应用场景包括：

回归模型效果评价：常用于衡量线性回归、多项式回归等模型的解释力。
经济和金融数据分析：例如评估某些经济指标对 GDP 增长的解释力。
机器学习模型调优：用于评估模型的拟合程度，帮助选择合适的模型或调参。

6. 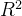$R^2$ 与其他误差指标的对比

指标	$R^2$	MAE、RMSE
计算方式	残差平方和和总平方和之比	绝对误差或平方误差
值域	[0, 1]（可能为负数）	非负值
异常值敏感性	高	MAE 低，RMSE 高
解释力	表示模型解释的变异比例	表示模型预测误差的均值

7.Python 实现代码

以下是计算 $R^2$ 的 Python 代码：

import numpy as np

def r2_score(y_true, y_pred):
    ss_res = np.sum((y_true - y_pred) ** 2)
    ss_tot = np.sum((y_true - np.mean(y_true)) ** 2)
    return 1 - (ss_res / ss_tot)

# 示例
y_true = np.array([3, -0.5, 2, 7])
y_pred = np.array([2.5, 0.0, 2, 8])

result = r2_score(y_true, y_pred)
print("R^2:", result)

说明

y_true 是真实值的数组，y_pred 是预测值的数组。
ss_res 是残差平方和，表示误差的总量。
ss_tot 是总平方和，表示目标变量的总变异。
1 - (ss_res / ss_tot) 得出 $R^2$ 值，表示模型对数据变异的解释程度。

图中 $R^2$ 的值接近 1 表示模型的预测接近真实值，具有较高的解释力。

8.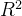 $R^2$ 图解示例

下面将生成一个包含 $R^2$ 计算图解的图示，以便更清楚地理解 $R^2$ 在模型解释力上的作用。

上图展示了 $R^2$ 的计算过程，其中：

蓝色圆点连线表示真实值 $y$ 。
红色叉点连线表示模型的预测值 $\hat{y}$ 。
每条灰色虚线表示预测值与真实值之间的差距，即残差。

# Re-import necessary libraries due to session context reset
import numpy as np
import matplotlib.pyplot as plt

# Generate sample data for illustration
np.random.seed(0)
x = np.linspace(0, 10, 10)
y_true = 2 * x + 1                       # True relationship (e.g., ground truth values)
y_pred = y_true + np.random.normal(0, 2, 10) # Predicted values with random noise

# Calculate R^2
ss_res = np.sum((y_true - y_pred) ** 2)   # Residual sum of squares
ss_tot = np.sum((y_true - np.mean(y_true)) ** 2) # Total sum of squares
r2_value = 1 - (ss_res / ss_tot)

# Plotting true vs predicted values and lines indicating residuals
plt.figure(figsize=(10, 6))
plt.plot(x, y_true, label="True Values", color="blue", marker='o')
plt.plot(x, y_pred, label="Predicted Values", color="red", marker='x')
plt.hlines(np.mean(y_true), x[0], x[-1], colors='green', linestyles='dashed', label='Mean of True Values')

# Add residual lines
for i in range(len(x)):
    plt.plot([x[i], x[i]], [y_true[i], y_pred[i]], color='gray', linestyle='dotted')

# Adding text and labels
plt.xlabel("x")
plt.ylabel("y")
plt.title(f"Illustration of R² (Coefficient of Determination)\nR² = {r2_value:.2f}")
plt.legend()
plt.grid(True)
plt.show()

为了更直观地理解 $R^2$ ，我们可以用一个散点图展示真实值和预测值的分布：