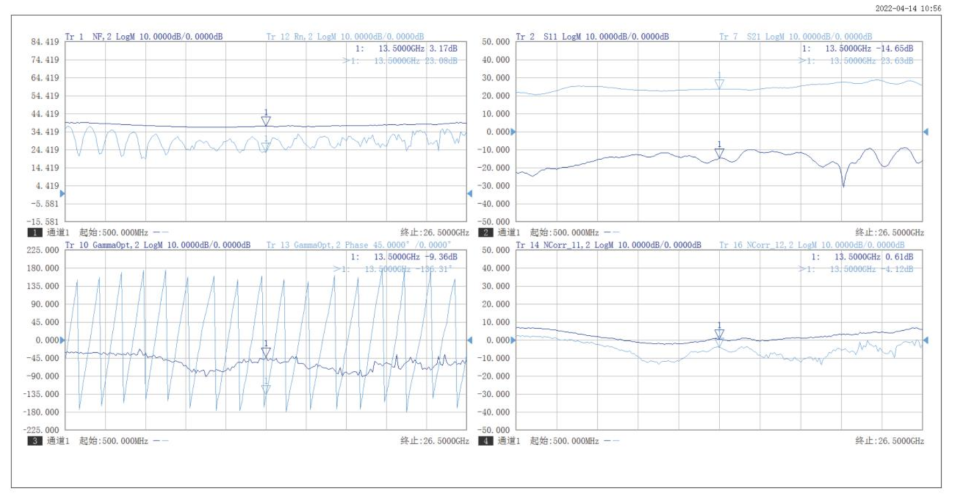
在多锚点定位系统中,锚点的选择对定位精度有重要影响。以下是几种常见的锚点选优方法,配合相应的公式和MATLAB代码示例进行详细分析。
文章目录
- 基于几何分布的选择
- 基于距离最小化的选择
- 加权优化选择
- 总结
基于几何分布的选择
方法描述:
锚点的几何分布影响定位的可辨识性。选择位置均匀分布的锚点组合可以提高定位精度。锚点之间的角度和距离应该尽可能大。
以下公式可以通过计算锚点之间的最小角度来评估锚点组合的几何分布:
θ = arccos ( ( x 2 − x 1 ) ( x 3 − x 1 ) + ( y 2 − y 1 ) ( y 3 − y 1 ) ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 ⋅ ( x 3 − x 1 ) 2 + ( y 3 − y 1 ) 2 ) \theta = \arccos\left(\frac{(x_2 - x_1)(x_3 - x_1) + (y_2 - y_1)(y_3 - y_1)}{\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \cdot \sqrt{(x_3 - x_1)^2 + (y_3 - y_1)^2}}\right) θ=arccos((x2−x1)2+(y2−y1)2⋅(x