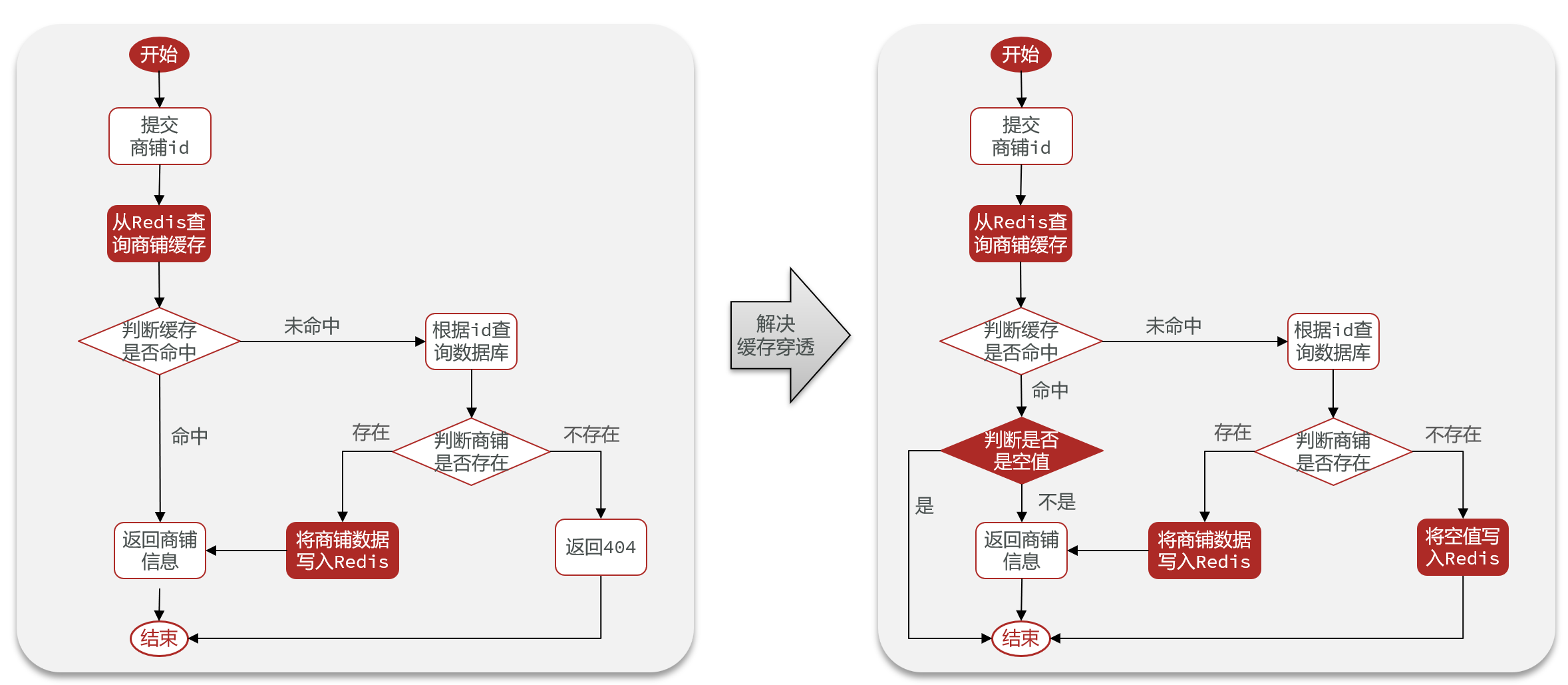
有关反向传播与梯度下降:流程与公式推导
- 背景
- 前向传播
- 反向传播
背景
反向传播则是一种训练神经网络的算法,目前我们使用的深度学习模型大都是通过这种方法训练的。它的核心思想是通过计算损失函数相对于每个参数的导数,来更新神经网络中的权重和偏置。反向传播负责计算梯度,梯度下降负责利用这些梯度来更新参数。两者的区别就是它们的目的不同:梯度下降是为了更新模型的权重和偏置;反向传播是为了在神经网络中获取损失函数关于每一层参数的导数(即每一层神经网络权重的梯度),为梯度下降提供依据。
前向传播
我们首先回顾一个简单的神经网络,使用两个输入,隐藏层有两个神经元(带有ReLU激活函数),以及一个预测(输出层):

每个隐藏神经元都在执行以下过程:

其中,input是我们输入的特征。weights是我们用来乘以输入的系数,我们算法的目标就是找到最优权重。Linear Weighted Sum将输入和权重的乘积相加,并加上一个偏置项b。之后经过一个激活函数增加非线性,ReLU是最常用的激活函数。
在我们上面提到的那个简单的神经网络中,hidden layer存储了多个神经元以学习数据模式。一个神经网络有可能是多层的,即包含多个hidden layers。
要训练一个神经网络,首先要让它生成预测,这被称为前向传播,即数据从第一层到最后一层(也称为输出层)遍历所有神经元的过程。以我们提到的简单的神经网络作为例子,我们首先为其创建一些任意的权重、偏置和输入:Input:
[
0.9
,
1.0
]
[0.9, 1.0]
[0.9,1.0]、输入到隐藏层的权重
W
1
W_1
W1:神经元1:
W
1
,
1
=
[
0.2
,
0.3
]
W_{1,1}= [0.2, 0.3]
W1,1=[0.2,0.3]
神经元2:
W
1
,
2
=
[
0.4
,
0.5
]
W_{1,2}=[0.4, 0.5]
W1,2=[0.4,0.5]、隐藏层偏置
b
1
:
[
0.1
,
0.2
]
b_1:[0.1, 0.2]
b1:[0.1,0.2]、隐藏层到输出层的权重
W
2
:
[
0.5
,
0.6
]
W_2:[0.5, 0.6]
W2:[0.5,0.6]、输出层偏置
b
2
:
[
0.4
]
b_2:[0.4]
b2:[0.4]。target/label设置为
[
2.0
]
[2.0]
[2.0]。
初始化之后,我们现在可以进行前向传播,过程如下:从输入到隐藏层的线性加权和
z
1
1
z¹_{1}
z11和
z
2
1
z¹_{2}
z21为:
z
1
1
=
W
1
,
1
⋅
I
n
p
u
t
+
b
1
,
1
=
[
0.2
,
0.3
]
⋅
[
0.9
,
1.0
]
+
0.1
=
0.58
z¹_{1}=W_{1,1}\cdot Input+b_{1,1}=[0.2,0.3]\cdot[0.9,1.0]+0.1=0.58
z11=W1,1⋅Input+b1,1=[0.2,0.3]⋅[0.9,1.0]+0.1=0.58
z
1
1
=
W
1
,
2
⋅
I
n
p
u
t
+
b
1
,
2
=
[
0.4
,
0.5
]
⋅
[
0.9
,
1.0
]
+
0.2
=
1.06
z¹_{1}=W_{1,2}\cdot Input+b_{1,2}=[0.4,0.5]\cdot[0.9,1.0]+0.2=1.06
z11=W1,2⋅Input+b1,2=[0.4,0.5]⋅[0.9,1.0]+0.2=1.06 然后,我们再隐藏层执行ReLU激活函数,得到
a
1
,
1
1
a^1_{1,1}
a1,11和
a
1
,
2
1
a^1_{1,2}
a1,21,然后生成整个网络的输出,这一步不涉及激活函数:
z
1
2
=
W
2
⋅
[
a
1
,
1
1
,
a
1
,
2
1
]
+
b
2
=
[
0.5
,
0.6
]
⋅
[
0.58
,
1.06
]
+
0.4
=
1.326
z^{2}_1=W_2\cdot[a^1_{1,1},a^1_{1,2}]+b_2=[0.5,0.6]\cdot[0.58,1.06]+0.4=1.326
z12=W2⋅[a1,11,a1,21]+b2=[0.5,0.6]⋅[0.58,1.06]+0.4=1.326 现在,我们就完成了第一次前向传播。这个过程可以直观地展示出来:

反向传播
完成前向传播后,我们拿到了网络的预测,我们希望通过预测和真实值的误差更新网络权重和偏置,以最小化网络预测结果的误差,这一步是通过反向传播算法实现的。
接下来,让我们深入了解这一算法的原理,反向传播旨在计算每个权重和偏置相对于误差(损失)的偏导数。然后,使用梯度下降法更新每个参数,从而最小化每个参数引起的误差(损失)。我们通过一个使用计算图的“简单”例子来说明。考虑以下函数:
f
(
x
,
y
,
z
)
=
z
(
x
−
y
)
f(x,y,z)=z(x-y)
f(x,y,z)=z(x−y) 我们将其绘制为计算图:

这是一个关于如何计算
f
(
x
,
y
,
z
)
f(x,y,z)
f(x,y,z)的流程图,将
p
p
p表示为
x
−
y
x-y
x−y,现在,让我们代入一些数值:

计算 f(x,y,z) 的最小值需要使用微积分,特别是,我们需要知道
f
(
x
,
y
,
z
)
f(x,y,z)
f(x,y,z)关于其三个变量
x
、
y
、
z
x、y、z
x、y、z的偏导数。我们可以从计算
p
=
x
−
y
p=x-y
p=x−y和
f
=
p
z
f=pz
f=pz的偏导数开始:
p
=
x
−
y
∂
p
∂
x
=
1
,
∂
p
∂
y
=
1
p=x-y\ \ \ \ \ \ \frac{\partial p}{\partial x}=1,\frac{\partial p}{\partial y}=1
p=x−y ∂x∂p=1,∂y∂p=1
f
=
p
z
∂
f
∂
p
=
z
,
∂
f
∂
z
=
p
f=pz\ \ \ \ \ \ \frac{\partial f}{\partial p}=z,\frac{\partial f}{\partial z}=p
f=pz ∂p∂f=z,∂z∂f=p 进一步地,我们使用链式法则来求解这些偏导:
∂
f
∂
x
\frac{\partial f}{\partial x}
∂x∂f、
∂
f
∂
y
\frac{\partial f}{\partial y}
∂y∂f、
∂
f
∂
z
\frac{\partial f}{\partial z}
∂z∂f,以x为例:
∂
f
∂
x
=
∂
f
∂
p
⋅
∂
p
∂
x
=
z
\frac{\partial f}{\partial x}=\frac{\partial f}{\partial p}\cdot \frac{\partial p}{\partial x}=z
∂x∂f=∂p∂f⋅∂x∂p=z 通过这种方式,我们对
y
,
z
y,z
y,z进行同样的操作,求得
∂
f
∂
y
=
z
\frac{\partial f}{\partial y}=z
∂y∂f=z、
∂
f
∂
z
=
x
−
y
\frac{\partial f}{\partial z}=x-y
∂z∂f=x−y,现在,我们可以在计算图上写下这些梯度及其对应的值:

请注意,在训练网络的过程中,我们的期望是最小化损失函数,那么这里的
f
(
x
,
y
,
z
)
f(x,y,z)
f(x,y,z)就相当于我们的损失函数,梯度下降法通过沿梯度的反方向更新值
(
x
,
y
,
z
)
(x,y,z)
(x,y,z)的一个小量来工作。例如,对于 x:
x
:
=
x
−
h
∂
f
∂
x
x:=x-h\frac{\partial f}{\partial x}
x:=x−h∂x∂f 那么这里的
h
h
h指的就是学习率,它决定了我们优化速度地大小,当我们将学习率设置为0.1,那么x被更新为3.7,我们再来观察现在的输出:

输出变小了,也就是说,它正在被最小化!现在,让我们将这个过程应用到上面提到的简单神经网络示例中。请记住,我们的预测值是 1.326,假设目标值是 2.0。以均方误差作为损失函数:
l
o
s
s
=
0.5
(
z
1
2
−
t
a
r
g
e
t
)
2
=
0.5
(
1.326
−
2
)
2
=
0.37826
loss = 0.5(z_1^{2} - target)^2 = 0.5(1.326 - 2)^2 = 0.37826
loss=0.5(z12−target)2=0.5(1.326−2)2=0.37826 请注意,在我们网络中使用的符号,上标表示层数。接下来,我们要计算损失相对于预测值的梯度:
∂
l
o
s
s
∂
z
1
2
=
z
1
2
−
t
a
r
g
e
t
=
−
0.674
\frac{\partial loss}{\partial z_1^{2}}=z_1^{2}-target=-0.674
∂z12∂loss=z12−target=−0.674 现在,我们需要计算损失相对于输出层偏置和权重(W_2 和 b_2)的梯度:
∂
l
o
s
s
∂
W
2
,
1
=
∂
l
o
s
s
∂
z
1
2
⋅
∂
z
1
2
∂
W
2
,
1
=
−
0.674
×
0.58
=
−
0.39092
\frac{\partial loss}{\partial W_{2,1}} = \frac{\partial loss}{\partial z_1^{2}} \cdot \frac{\partial z_1^{2}}{\partial W_{2,1}} = -0.674 \times 0.58 = -0.39092
∂W2,1∂loss=∂z12∂loss⋅∂W2,1∂z12=−0.674×0.58=−0.39092
∂
l
o
s
s
∂
W
2
,
2
=
∂
l
o
s
s
∂
z
1
2
⋅
∂
z
1
2
∂
W
2
,
2
=
−
0.674
×
1.06
=
−
0.71444
\frac{\partial loss}{\partial W_{2,2}} = \frac{\partial loss}{\partial z_1^{2}} \cdot \frac{\partial z_1^{2}}{\partial W_{2,2}} = -0.674 \times 1.06 = -0.71444
∂W2,2∂loss=∂z12∂loss⋅∂W2,2∂z12=−0.674×1.06=−0.71444
∂
l
o
s
s
∂
b
2
=
∂
l
o
s
s
∂
z
1
2
⋅
∂
z
1
2
∂
b
2
=
−
0.674
×
1
=
−
0.674
\frac{\partial loss}{\partial b_2} = \frac{\partial loss}{\partial z_1^{2}} \cdot \frac{\partial z_1^{2}}{\partial b_2} = -0.674 \times 1 = -0.674
∂b2∂loss=∂z12∂loss⋅∂b2∂z12=−0.674×1=−0.674 这些表达式看起来可能很复杂,但我们其实只是进行了部分微分,并多次应用了链式法则,根据这一公式:
z
1
2
=
W
2
,
1
×
a
1
1
+
W
2
,
2
×
a
2
1
+
b
2
z_1^{2}=W_{2,1}\times a_1^{1}+W_{2,2}\times a_2^{1}+b_2
z12=W2,1×a11+W2,2×a21+b2 最后一步是使用梯度下降法更新参数,学习率设置为
h
=
0.1
h=0.1
h=0.1:
W
2
,
1
:
=
W
2
,
1
−
h
∂
(
loss
)
∂
(
W
2
,
1
)
=
0.5
−
(
0.1
)
(
−
0.39092
)
=
0.539092
W_{2,1} :=W_{2,1} - h \frac{\partial (\text{loss})}{\partial (W_{2,1})}=0.5 - (0.1)(-0.39092)=0.539092
W2,1:=W2,1−h∂(W2,1)∂(loss)=0.5−(0.1)(−0.39092)=0.539092
W
2
,
2
:
=
W
2
,
2
−
h
∂
(
loss
)
∂
(
W
2
,
2
)
=
0.6
−
(
0.1
)
(
−
0.71444
)
=
0.671444
W_{2,2} :=W_{2,2} - h \frac{\partial (\text{loss})}{\partial (W_{2,2})}=0.6 - (0.1)(-0.71444)=0.671444
W2,2:=W2,2−h∂(W2,2)∂(loss)=0.6−(0.1)(−0.71444)=0.671444
b
2
:
=
b
2
−
h
∂
(
loss
)
∂
(
b
2
)
=
0.4
−
(
0.1
)
(
−
0.674
)
=
0.4674
b_2 :=b_2 - h \frac{\partial (\text{loss})}{\partial (b_2)}=0.4 - (0.1)(-0.674)=0.4674
b2:=b2−h∂(b2)∂(loss)=0.4−(0.1)(−0.674)=0.4674 我们已经更新了输出层的权重和偏置!接下来,我们要对隐藏层的权重和偏置重复这个过程,并使用梯度下降法更新这些权重:
w
1
,
1
:
=
w
1
,
1
−
h
∂
l
o
s
s
∂
w
1
,
1
=
0.23033
w_{1,1}:=w_{1,1}-h\frac{\partial loss}{\partial w_{1,1}}=0.23033
w1,1:=w1,1−h∂w1,1∂loss=0.23033
w
1
,
2
:
=
w
1
,
2
−
h
∂
l
o
s
s
∂
w
1
,
2
=
0.3337
w_{1,2}:=w_{1,2}-h\frac{\partial loss}{\partial w_{1,2}}=0.3337
w1,2:=w1,2−h∂w1,2∂loss=0.3337
b
1
:
=
b
1
−
h
∂
l
o
s
s
∂
b
1
=
0.1337
b_1:=b_1-h\frac{\partial loss}{\partial b_1}=0.1337
b1:=b1−h∂b1∂loss=0.1337
w
2
,
1
:
=
w
2
,
1
−
h
∂
l
o
s
s
∂
w
2
,
1
=
0.4364
w_{2,1}:=w_{2,1}-h\frac{\partial loss}{\partial w_{2,1}}=0.4364
w2,1:=w2,1−h∂w2,1∂loss=0.4364
w
2
,
2
:
=
w
2
,
2
−
h
∂
l
o
s
s
∂
w
2
,
2
=
0.54044
w_{2,2}:=w_{2,2}-h\frac{\partial loss}{\partial w_{2,2}}=0.54044
w2,2:=w2,2−h∂w2,2∂loss=0.54044
b
2
:
=
b
2
−
h
∂
l
o
s
s
∂
b
2
=
0.24044
b_2:=b_2-h\frac{\partial loss}{\partial b_2}=0.24044
b2:=b2−h∂b2∂loss=0.24044 这样,我们就进行了一次完整的反向传播迭代!对于训练集中所有样本的一次前向传播和一次反向传播构成一个训练周期(epoch)。下一步是使用更新后的权重和偏置进行另一次前向传播,使用新权重和偏置的前向传播结果为1.618296,这更接近目标值 2,因此网络已经“学习”到了更好的权重和偏置,这就是机器学习的实际应用。