将激光雷达点云投影到相机图像上做数据层的前融合，或者把激光雷达坐标系下标注的物体点云的3d bbox投影到相机图像上画出来，都需要做点云3D点坐标到图像像素坐标的转换计算，也就是LiDAR 3D坐标转像素坐标。

看了网上一些文章都存在有错误或者把公式推导说的含混不清有误导人的地方(如果你完全按那些列出来的公式去计算，发现投影结果在图像上怎么都不对！)，在此结合我经过验证是正确的代码详细解释一下，也供备忘，插图是对网上的原图做了正确修改的。

对于普通无畸变平面相机，坐标转换涉及到的主要是两个参数矩阵：用于激光雷达坐标系到相机坐标系转换的外参矩阵和用于相机坐标系到像素坐标系转换的相机本身的内参矩阵。

针孔相机模型下，相机坐标系下的三维空间中点P(X,Y,Z)，对应在相机成像平面的图像坐标系(注意不是像素坐标系!)中的坐标点是p(x,y)，焦距f是焦点到成像平面之间的距离，Z是P点到焦点的距离。

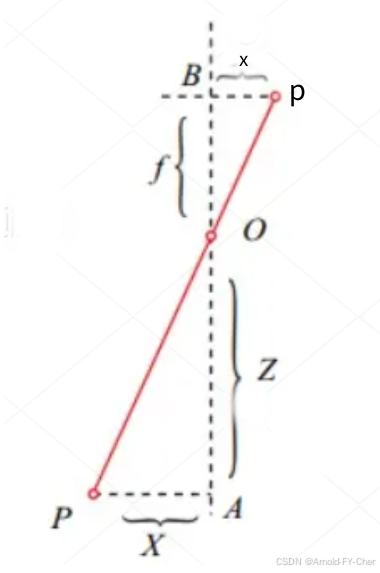
 根据相似三角形原理，有：

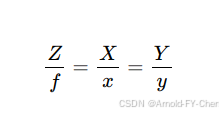
 由此可得，根据相机坐标系下的坐标(X,Y,Z)计算相机图像坐标系下的坐标(x,y)的计算公式：

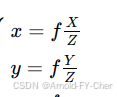
注意，此处的x、y、f都是实际空间尺寸，单位一般是mm，如果将等式两边都除以图像每像素对应的实际尺寸，等式仍然成立，此时的x、y、和f就都是像素了，所以我们平时看到的数据集里camera的焦距值都是像素值，正是我们计算像素为单位的x和y所需的，然后，因为把图像坐标坐标系下的像素为单位的坐标(x,y)转像素坐标系下的坐标(u,v)，只需加上图像横纵方向各自的偏移量cx和cy即可(因为图像坐标系的原点是在图像的中央，而像素坐标系的原点是在图像的左上顶点)，另外相机的纵横方向的焦距稍有差异，不是同一个f值，所以还区分为fx和fy，至此，稍做推导可以得出相机坐标系下的坐标P(X,Y,Z)转换为图像上的像素坐标的计算公式为:

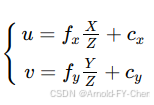
整理成矩阵运算形式就是:

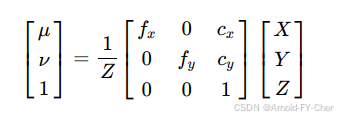
其中相机内参矩阵就是:

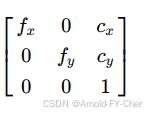
将激光雷达坐标系下的3D点坐标转换到相机图像上的像素坐标的过程就是先将激光雷达坐标系下的3D坐标(Xw,Yw,Zw)(此处假设雷达不动或者我们只关注激光雷达坐标系下的坐标转换到像素坐标，(Xw,Yw,Zw)表示激光雷达坐标系下的坐标，此处的(Xw,Yw,Zw)不是激光雷达坐标而是导航用的世界坐标系下的坐标的话，下面的表示是错的，需要先用global2ego之类参数矩阵将坐标转换到雷达坐标系下)，左乘以lidar2camera相机外参矩阵转换到相机坐标系下的3D坐标(Xc,Yc,Zc):

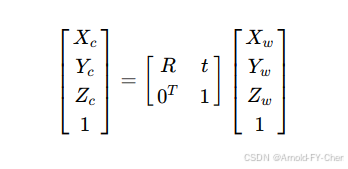
然后如上面所述使用相机本身的内参矩阵将相机坐标系下的3D坐标点转换到像素坐标系下的像素坐标，于是整个计算可以合并表示为(此处的fx、fy、Cx、Cy都是像素为单位的值！)：

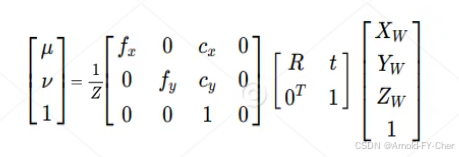
很多文章里列出连乘公式都漏了这个重要的 ，导致计算出来的像素坐标根本不对(把像素坐标点在图像上画出来看图像上的点投影效果比较直观)，包括一些BEV模型的实现代码都犯了这个错误，效果能好才怪！这个转换关系(K是相机内参矩阵)要记住：

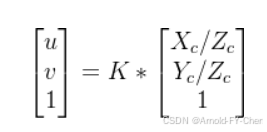
这里的Z就是相机坐标系下的3D坐标(Xc,Yc,Zc)的Zc，上面倒数第三个公式里也说明了。那么我们代码实现时，对于普通无畸变平面相机，非常简单，就是 (1/Z) X 相机的内参矩阵 X 相机的外参矩阵(lidar2camera)，即可由激光雷达下的3D坐标计算出像素坐标系下的坐标，用我写的经过验证是正确的C++代码作为示例，借助Eigen库实现非常简单：

    Eigen::Vector4f pointVec;
    pointVec << point3D, 1.0;

    Eigen::Vector4f cam_point3D =  K * extrinK * pointVec;
    Eigen::Vector3f point = cam_point3D.head<3>();
    float x = point.x();
    float y = point.y();
    float z = point.z();
    if (z < 1e-6) {
       return;
    }
    int u = static_cast<int>(x / z);
    int v = static_cast<int>(y / z);

上面K是4x4奇次相机内参矩阵，extrinK是4x4奇次外参矩阵，算出来的部分u,v值有的可能超出了相机图像的范围，用图像的cols和rows最大值最小值过滤一下就可以了，对于BEV模型，投影到6个相机的图像上使用各个相机各自的内外参矩阵依次做上述计算即可。

对于有畸变的平面相机，则不能使用内参和外参矩阵连乘，而是需要先左乘以外参矩阵把点云3D坐标转到相机坐标系下的坐标(Xc,Yc,Zc)后，把Zc小于等于0的坐标过滤掉，然后需要把Xc和Yc除以Zc，得到未校正的相机坐标系下的2D坐标(Xc/Zc,Yc/Zc)，然后根据相机厂家给出的计算公式使用相机的畸变系数对此2D坐标做校正得出校正后的坐标(X,Y)，再将此坐标扩展为奇次坐标后转置再左乘以相机的3x3原始内参矩阵，得出像素坐标(u,v)，可以参考相机标定之畸变矫正与反畸变计算 - 达达MFZ - 博客园这篇文章给出的去畸变算法的实现，代码如果借助Eigen矩阵运算，可以写得更简洁点，不过他这样写的好处就是比较容易看清楚。车载森云相机的去畸变就是这样的算法，我们借助Eigen库自己实现的代码涉及到商业秘密就不列出来了。

多说一点就是，根据上面的计算公式:

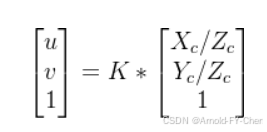
假设我们知道每个像素的深度值Zc的话，可以由下面的公式计算出图像里每个像素对应的相机坐标系下的3D点坐标(Xc,Yc,Zc) :

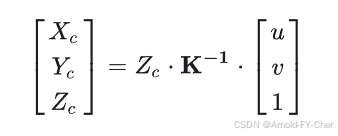
这就是LSS模型预测每像素的深度后获得对应的3D点坐标的计算原理，从而实现2D到3D的对应转换，进而Splat成BEV。