基于排名的股票预测的关系时态图卷积网络(RT-GCN)

“ 为了充分利用股票之间的关系，获得最高收益，提出了一种关系时态图卷积网络(RT-GCN)。”

标题：Relational Temporal Graph Convolutional Networks for Ranking-Based Stock Prediction

链接：https://ieeexplore.ieee.org/document/10184655

会议：ICDE

摘要：

股票预测是《金融科技》中颇具吸引力的话题。然而，传统的股票预测方法存在两个缺陷：(1)一些方法侧重于股票的时间模式，将每只股票建模为独立的个体，而忽略了它们之间的关系。有些模型考虑了股票之间的关系，但采用两步法(即先捕捉时间模式，再考虑关系相关性)，使得模型复杂且效率低下；(2)它们将股票预测建模为回归(预测股价)或分类任务(预测股票趋势)，不能优化投资目标，即从未来预期收益最高的交易所市场中选择最好的股票。为了充分利用股票之间的关系，获得最高收益，提出了一种关系时态图卷积网络(RT-GCN)。我们首先将股票及其日常特征之间的关系建模为一个关系-时态图。然后，我们应用RTGCN和三种关系感知策略来实现对每只股票的关系时态特征提取。最后，以学习排名的方式反馈特征进行评分计算，得分最高的股票代表未来投资收益最高。大量实验证明了该方法的有效性和高效性

—

创新点

为了充分利用每只股票的关系和时间信息，我们将股票关系和每只股票的时间特征建模为关系时间图，这是RT-GCN应用的基础，也是我们模型高效的前提。
我们提出RT-GCN 用于基于排名的股票预测任务。该模型采用纯卷积结构构建，可同时捕获时间动态和关系依赖性，从而实现更快的训练速度。这样的改进对于短期股票交易系统来说意义重大。
我们在RT-GCN 中设计了三种关系感知传播策略来满足股票预测任务的需求。 • 在纳斯达克、纽约证券交易所和中证指数数据集上进行的大量实验表明，RT-GCN 在有效性和效率方面可以超越最先进的方法

—

RT-GCN模型架构

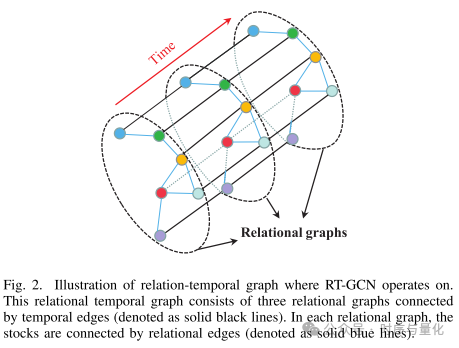
上图是最基本的RT-GCN的架构。RT-GCN 运行的关系时间图的图示。该关系时间图由通过时间边缘（表示为黑色实线）连接的三个关系图组成。在每个关系图中，股票通过关系边（表示为蓝色实线）连接。

我们提出的框架的插图。RT-GCN模块上方的循环标志代表RT-GCN网络可以堆叠成为更深的网络。

每个关系-时间图卷积层(RT-GCN)由关系卷积结构和时间卷积结构组成，输入数据将首先经过关系卷积，然后经过时间卷积。关系卷积结构旨在通过聚合其邻居信息和利用时间卷积结构来丰富每个节点的表示，以通过跨连续时间步提取关键信息来压缩时间维度。在 RT-GCN 层之后添加平均池化层以生成每只股票的表示。该表示将被馈送到全连接层以计算排名分数。整个模型通过反向传播以端到端的方式进行训练。我们将在下面详细介绍每个模块。

简单来说，模型主要关系卷积结构和时间卷积结构组成，然后添加时间池化层和全连接层计算股票排名分数。下面介绍这两个模块。

—

关系图卷积（Relational Graph Convolution）

提出了三种不同的策略来充分利用股票之间的这些关系。这三种策略是通过不同的关系感知函数R来实现的，R可以以关系矩阵为输入返回不同的加权邻接矩阵A。下面，我们详细介绍如何设计这三种策略。

1）统一策略：第一个策略是最简单的，它忽略了股票之间的不同关系，而对待股票之间的不同关系所有股票对都是相同的，因为这些不同的关系在图表中传播信息方面发挥着熟悉的作用。

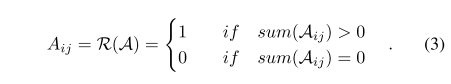
回想一下，是定义的关系矩阵，N为股票节点，K为边的类型，并且有了定义好的邻接矩阵A，GCN模型就可以对每个图关系卷积(GR)进行操作。请注意，在卷积过程中，不同时间步长的所有图关系卷积（关系-时序卷积图）共享相同的 A。

2）权重策略：然而，第一种策略是粗糙的，因为它忽略了不同的关系可能会导致两只股票之间不同的影响。为了克服这个缺点，我们在图上传播信息时应用非均匀系数，如下式所示：

其中 w 和 b 是要学习的参数。作为策略 1，在卷积过程中，不同时间步长的所有图关系卷积（关系-时序卷积图）也共享相同的 A。该策略更具关系性，因为它可以使用不同的关系向量作为输入返回不同的权重。

3）时间敏感策略：上述两种策略的共同限制是不同时间步长的所有关系图共享相同的权重。然而，股票市场是高度动态的，因此股票的状态和关系的强度可能会在不同的时间步长中不断变化。不同时间步长的所有关系图的固定权重无疑会限制我们的模型能力。例如，在前面图1(b)的例子中，苹果公司的股价在新版本产品发布期间对Lens股票的影响比平常更大。为了解决这个问题限制，我们将时间敏感的传播过程定义为等式：

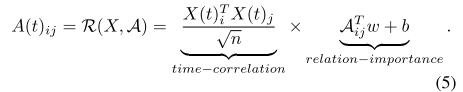
这里，，是股票i和j在时间步长t的特征，n是的维度，和b是可训练参数.

具体地说，第一项通过使用两只股票在当前时间步长的特征来衡量两只股票之间的相关性。我们采用缩放的点积来计算这一项，利用它来计算图中两个节点的权重。第二项与策略二·相同，返回关系向量的关系权重。与上述两种策略不同，该策略可以为GRT中的每个GR分配一个唯一的加权邻接矩阵。由于它同时考虑了两只股票之间的时间相关性和关系重要性，因此它是一种优势策略，比其他两种策略更适合于股票预测。

—

时间卷积（Temporal Convolution）

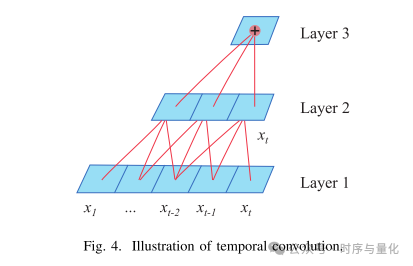
提出的时间卷积架构构建了时间卷积网络（TCN）模块。TCN 使用一维滤波器通过因果卷积来捕获时间依赖性，如图 4 所示，其中时间 t 的输出仅与前一层中时间 t 及更早时间的元素进行卷积，因此可以有没有从未来到过去的泄漏。例如，第 2 层中的仅与第 1 层中的、和进行卷积，并且不依赖于第 1 层中时间步 t + 1 和 t + 2 处的任何未来。这样，未来就不会泄漏到过去。为了捕获输入特征的较长距离依赖性，我们改变滤波器移动步幅以通过零填充扩展感受野组合。等式 (6) 给出了由滤波器操作的第 t 元素上的 TCN 数学表达式：

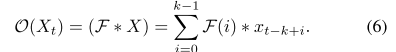
我们还在 TCN 层之后添加了残差连接 [，以简化网络训练并将权重归一化应用于卷积滤波器。此外，在每个 TCN 层之后添加了一个空间 dropout以进行正则化。

—

池化和预测（Pooling and Prediction）

经过 RT-GCN 处理后，我们可以获得关系时间图的关系时间特征，H 是时间卷积组件处理后的最终时间维度，N 是股票数量，F 是经过关系卷积组件处理后的库存特征维度。接下来，我们使用 stride=H 的平均池化层来生成每个股票的表示 (文章的这里我认为应该是）。最后，每只股票的表示将被输入到全连接层以计算排名分数。我们使用均方误差损失来优化模型，以最小化预测回报率和实际回报率之间的差异，并与成对排名感知损失配合，以维持排名股票的相对顺序。

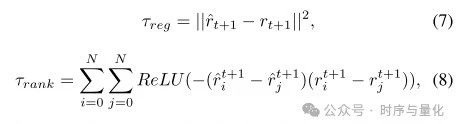
其中，是真实排名，是预测排名分数，RELU是激活函数。因此，我们的模型的最终损失函数可以写为Eq(9)：

其中，β是所有可学习参数的集合，λ是L2正则化的权重，α是回归损失和排名损失之间的平衡参数.

实验结果

—

实验（EXPERIMENTS）

数据集：

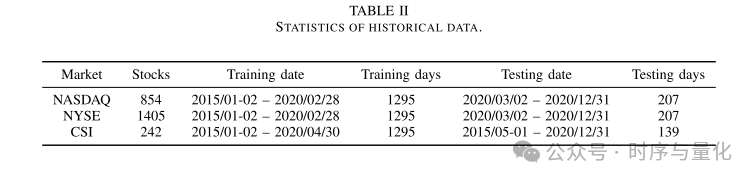
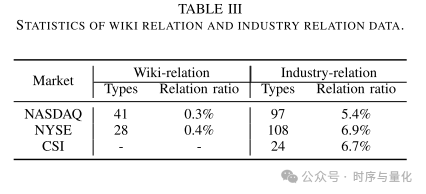
维基关联和行业关联数据统计。

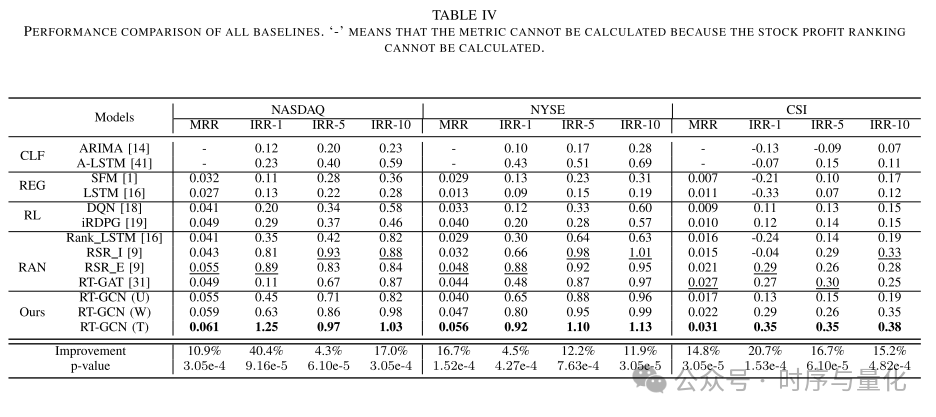
所有基线的性能比较。 “-”表示无法计算该指标，因为无法计算股票利润排名。

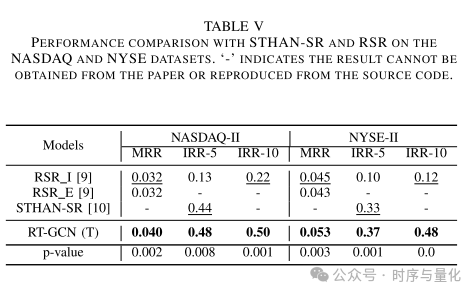
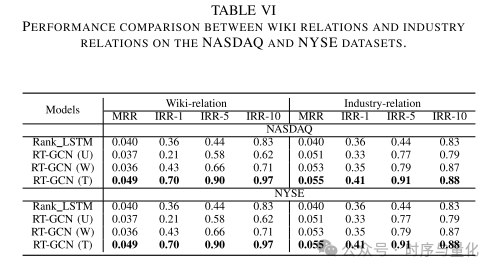
结论

—

结论（CONCLUSION）

提出了一种基于排名的股票预测的关系时间图卷积网络（RT-GCN），以充分利用股票之间的关系，实现股票投资的最高收益。我们首先将股票之间的关系及其每日特征建模为关系时间图。然后，我们应用图卷积网络和三种提出的关系感知策略来提取每个节点（股票）的关系时间特征。最后，将这些特征以学习排名的方式计算排名得分，得分最高的股票代表未来最高的投资收益。纳斯达克、纽约证券交易所和中证指数的实验结果证明了我们提出的模型的有效性和效率。

欢迎添加公众号，获取更多时间序列文章。