DOI: 10.1103/PhysRevLett.133.156702
摘要节选
与电子带的自旋分裂一样,预测交变磁体中的磁振子带也表现出交替的手性分裂。本文通过对α-MnTe进行非弹性中子散射(INS),直接观察到α-MnTe的磁振子分裂现象。磁振子的简并解除可以用对称交换起源很好地解释。根据得到的自旋波模型进一步计算表明,磁振子也是手性分裂的。此外,还通过实验确定了MnTe的g波磁性
引言节选
交变磁体中明显的自旋对称性在保持补偿自旋排列的同时打破了时间反转对称性(TRS)。因此,即使在没有相对自旋轨道耦合的情况下,交变磁体中的电子带也是自旋分裂的。
通过角分辨光发射光谱在交变磁候选MnTe , RuO2和CrSb中观察到能带的极化。
除能带分裂外,交变磁体还表现出与TRS断裂性质相关的各种奇异量子现象,如反常霍尔效应、电荷-自旋电流转换、自旋分裂扭矩、磁性圆二色性和压磁效应。
与电子带的自旋分裂类似,在考虑对称交换相互作用的情况下,理论上预测交变磁振子会表现出手性分裂。
结果与讨论
α-MnTe
空间群P63/mmc
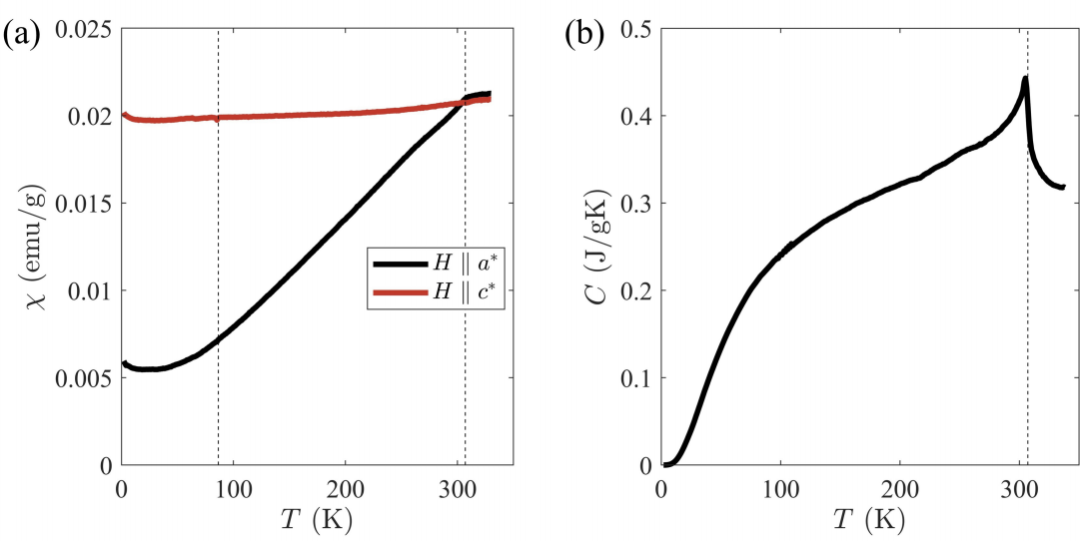
TN=307 K
a = b = 4:148Å, c = 6:712Å
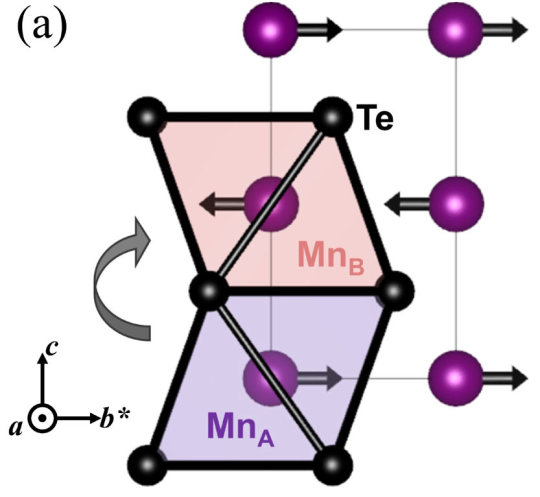
A型反铁磁(AFM)基态,其中Mn2+离子的自旋S=5/2在ab平面沿晶体b轴呈铁磁取向,并在相邻层之间呈反铁磁排列。两个相反自旋的子晶格,MnA和MnB,通过实空间镜像或六倍旋转对称连接。
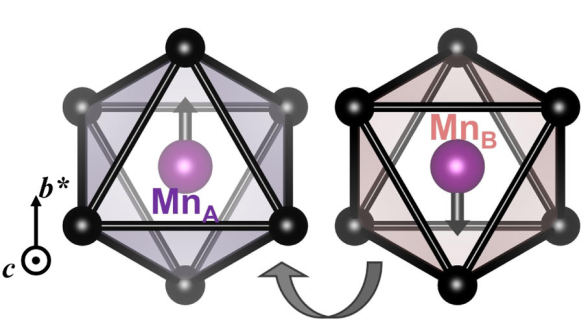
相反自旋亚晶格MnA和MnB通过镜像操作或六倍旋转连接,而不是任何平移或反转,这符合交变磁体的分类
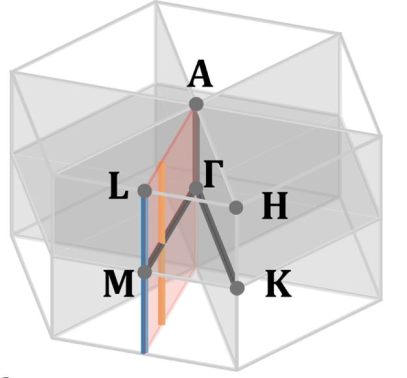
除了布里渊区(BZ)边界外,镜像和六重旋转对称保护了四个节点平面(NPs)中的电子带的简并性。MnTe的体敏x射线角分辨光发射光谱显示,在NPs的电子带中出现了1/2 eV尺度的自旋分裂,表明MnTe存在显著的交变磁效应。
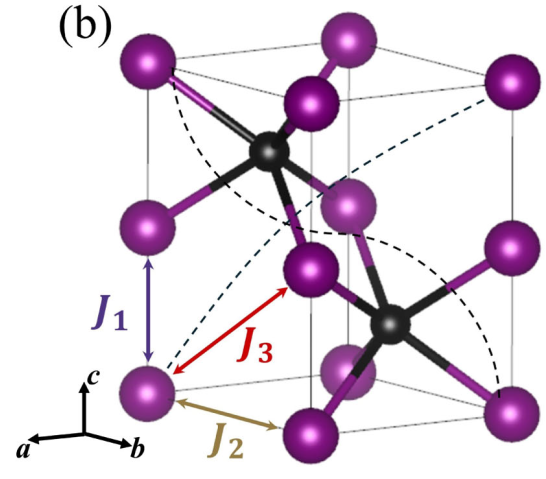
基于自旋对称性,分析了MnTe中的交替磁超交换相互作用为第十和第十一近邻相互作用J10和J11,它们交替地通过多个Te连接相同的自旋子晶格,如上图中的虚线所示。
虽然J10和J11的远距相互作用不可避免地很弱,但由于通过Te轨道的交换路径不同,它们的值甚至符号也可能不同。
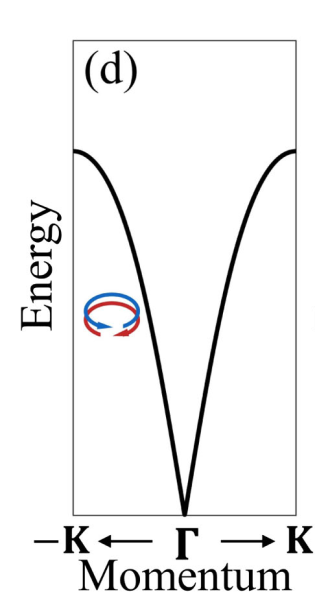
与电子带相似,手性磁振子的简并性也受到子晶格间对称性的保护。在NPs和BZ边界内,交替磁振子色散与传统AFM的磁振子色散相同,
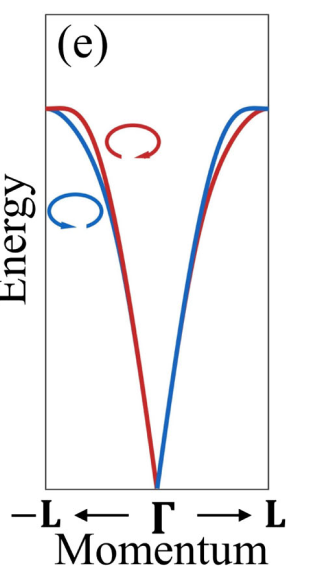
J10和J11之间的有限差异使磁振子简并远离NPs和BZ边界,而交变磁振子在Γ点附近仍然保持类似AFM的线性色散。在Γ点处,Mch为零。虽然易平面各向异性使磁振子在Γ点的双简并性得到提升,但由于TRS仍被保留,因此手性分裂是被禁止的。
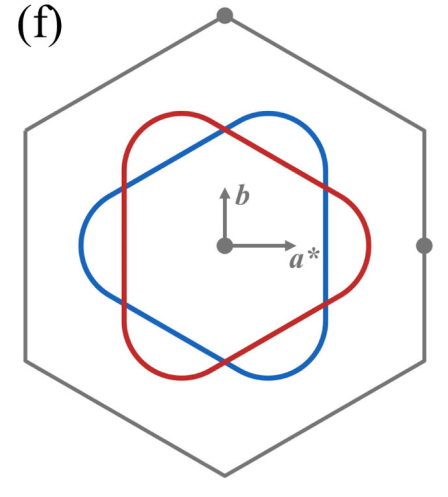
c*面非简并色散的常能量轮廓在MnTe中表现为g波谐波对称。
注意这些非简并色散也是交替的手性分裂。先前在MnTe上的INS实验受到相对宽松的能量分辨率的限制,只探测了第一、第二和第三近邻交换相互作用(记为J1、J2和J3),而忽略了磁振子色散的分裂特征。
为了实现INS,采用自通量法合成了大型MnTe单晶。
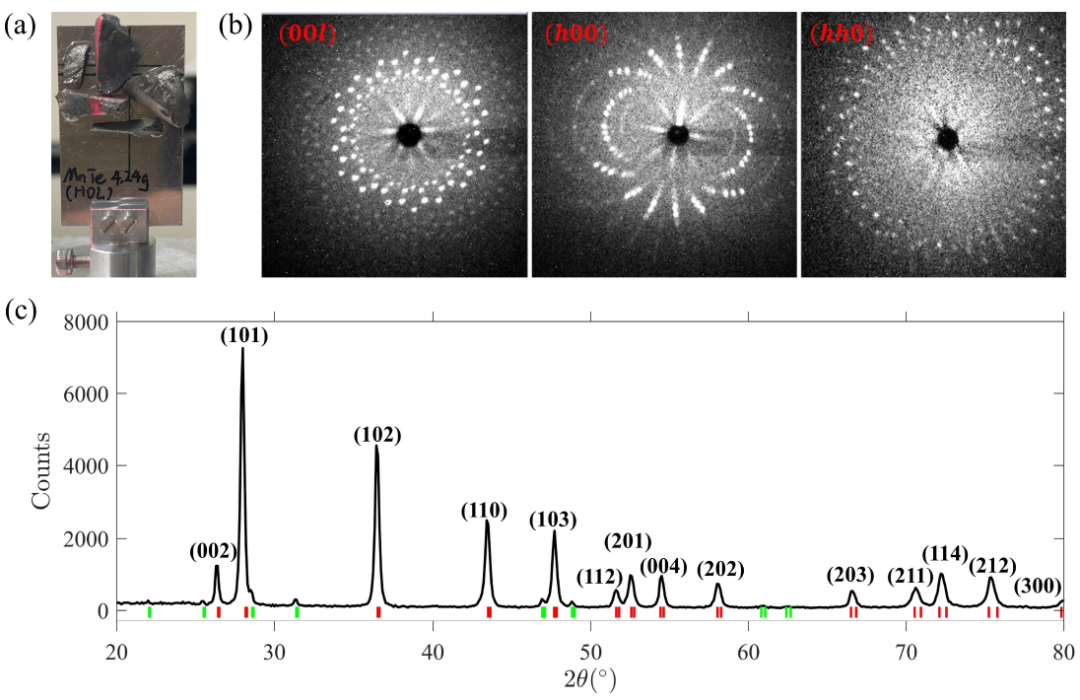
5个总质量为4.2 g的晶体在一个由(h,0,0)和(0,0,l)跨越的散射平面上排列。
在Ei为50.8 meV的INS实验中,观察到明确的磁振子激发。
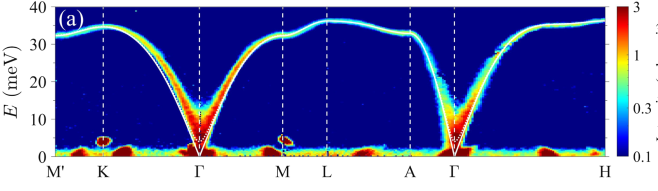
沿高对称Q路径的谱,M' (-1/2,1/2,1);K (-2/3,1/3,1) ;Γ (-1,0,1);L (-2/3,0,1);A (-1,0,3/2); Γ (-1,0,1);H (-1/2,1/2,3/2);都位于自旋体NPs内。
它表现出典型的类似AFM的磁振子色散,具有单离子易平面各向异性。在K点和M点附近E=5 meV的斑点被认为是伪影,因为它们在Ei=11.4 meV的光谱中不存在。
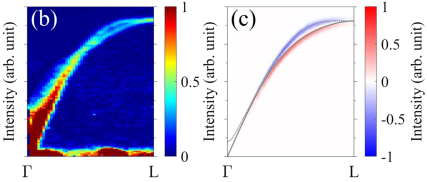
Γ−L方向谱图显示了在E ~ 30 meV以上的磁振子分裂,而色散在较低能量范围内保持线性特征。在自旋简并NP中,当接近Γ或L时,这种分裂逐渐消失。灰色实线和虚线表示计算出的两种磁振子模式。

在(-1.33,0,l)方向处明显观察到分裂色散。上图为INS谱和计算得到的结构因子和手性因子。两个非简并磁振子模式沿c*轴交替传播,在整数和半整数l处形成节点,这意味着Mn2+子晶格的镜像对称性。交替传播的磁振子色散也是交替的手性分裂。
作为比较,在沿BZ边界处(-1.5,0,l)测试和计算了类似的色散。
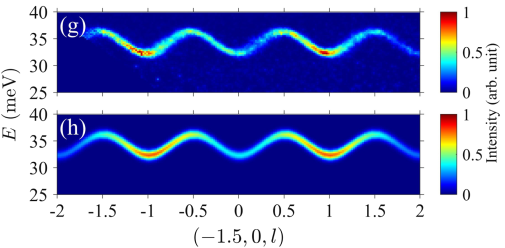
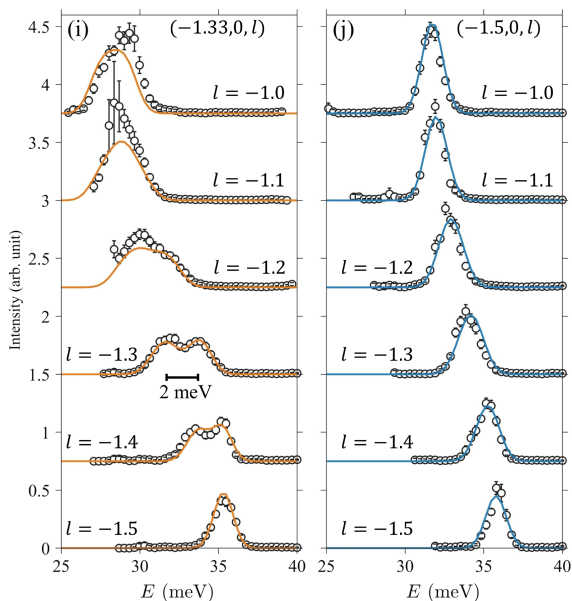
一维(1D)常数Q切割表明,在大多数中间l范围(- 1< l <-1.5)内,双峰分裂为2 meV。相反,在l=−1,−1.5和沿(-1.5,0,l)的每一个切口,激发为一个尖锐的单峰。
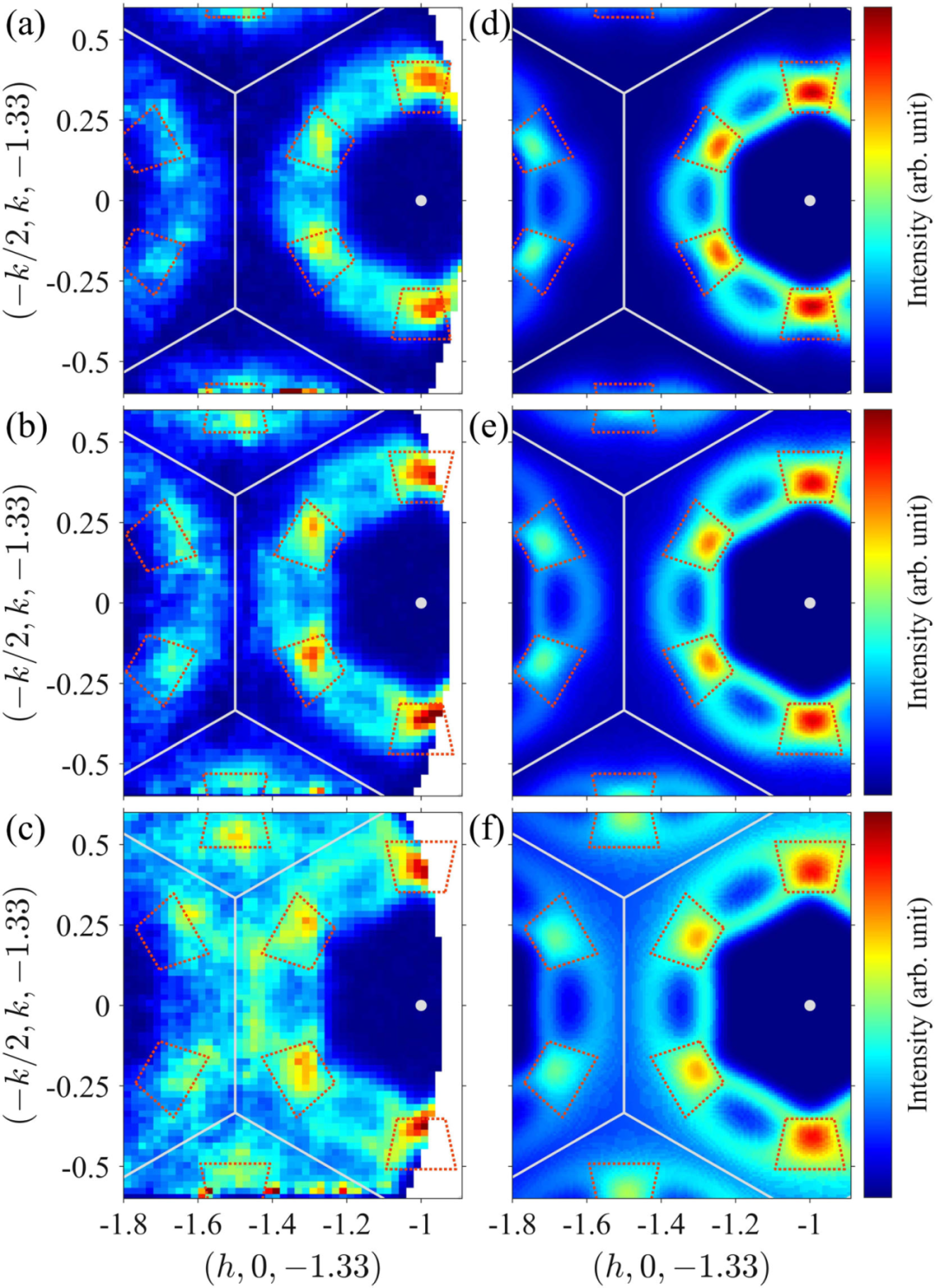
交替磁MnTe的g波谐波对称性是由Mn2+亚晶格之间不正确的六倍旋转引起的
这在非节位(h,k,-1.33)平面的的常E切片中得到了明确的验证。
在E=33 mev至34 mev范围内清晰地观察到6倍高强度节点。色散的分裂轮廓显示出典型的缠绕g波模式,再次将非常规的分裂与自旋对称联系起来。
方法
实验合成
采用flux法合成MnTe单晶。将摩尔成分为Mn0.436Te0.564,氧化铝坩埚,密封石英管中。
多余的Te用于将MnTe的结晶温度降低到1026℃以下的结构转变温度。1020℃,18h,0.9℃/h速度冷却到760℃。
非弹性中子散射INS实验
INS实验在J-PARC MLF BL-12的高分辨率斩波(HRC)光谱仪上进行。采用Gifford-McMahon型低温恒温器控制温度。费米斩波器的频率为200hz。在t10 K下测量的入射能量分别为50.8 meV和11.4 meV。HRC具有垂直的探测器组,因此可以进入散射平面外的动量(Q)空间。
自旋哈密顿量拟合
为了确定自旋哈密顿量,利用SpinW包基于线性自旋波理论(LSWT)进行了计算。由于变磁的概念属于对称交换相互作用的范畴,考虑具有单离子易平面各向异性的海森堡自旋哈密顿量,表示为
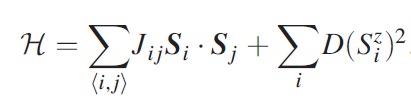
J1、J2和J3,以及更远的第4到第9近邻交换相互作用,都不能解释图中的分裂色散。
非常规的磁振子分裂也不是由相对论效应引起的;Dzyaloshinskii-Moriya相互作用在MnTe的中心对称晶格中不活跃。虽然单离子易平面各向异性提升了整个BZ的简并度,但劈裂能在Γ点以外减小,不能解释所观察到的劈裂。
因此,交替磁交换相互作用J10和J11在自旋哈密顿量中是至关重要的。
采用共线AFM自旋结构,在LSWT计算中采用S=5/2。
在MnTe中,通过磁有序形成了六个磁畴,其N´eel向量平行于晶体学b*轴。
计算的方法是考虑六个磁畴的平均分布。在NPs内部,J1、J2、J3、J10+J11和D是色散公式的参数。
通过加权最小二乘法拟合NPs中的谱,得到最佳解为J1= 3.99(3) meV, J2= −0.120(2) meV, J3= 0.472(3) meV,J10+J11= 0.0931(8) meV,D= 0.0482(5) meV。
其中,J10= 0.0681(7) meV和J11= −0.0221(2) meV。
虽然J10和J11的数值较小,但由于S的自旋值大,键的配位数大,分裂能与实验中观察到的一样大。
手性因子计算方法
利用LSWT计算了中子自旋哈密顿量的手性因子。表示为
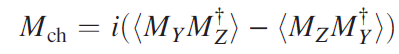
其中X平行于Q, Y与散射平面中的X正交,Z与散射平面正交。