摘要
本文研究了雪消融优化算法在二维路径规划问题中的应用。该算法基于自然界中雪消融现象的模拟,通过优化策略寻找无人机路径的最优解。实验结果表明,该算法在路径规划中表现出较高的效率和收敛速度,能够有效地避开障碍物并找到代价最低的路径。
理论
-
雪消融优化算法: 雪消融算法(SMA)模仿了自然界中雪在不同温度条件下融化的过程。该算法通过更新个体位置的方式,模拟了雪从冰冷坚固逐渐融化成液态的过程,从而达到优化目标。在路径规划问题中,目标是找到一条能够避开障碍物且距离最短的路径。
-
二维路径规划: 在二维平面上,为无人机寻找从起点到终点的最优路径,既要考虑路径的距离最短,又要避开可能存在的障碍物。SMA通过在解空间内随机搜索,结合模拟的雪消融过程不断逼近最优解。
实验结果
-
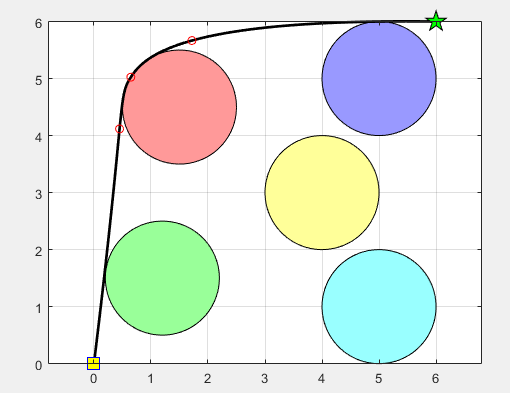
图1: 显示了SMA应用于二维路径规划的结果,红色的圆形代表障碍物,路径从起点(左下角黄色方块)到终点(右上角绿色五角星),黑色线表示通过SMA计算得到的最优路径。可以看到路径成功绕过了障碍物。
-
图2: 该图展示了SMA在多次迭代中的收敛情况。横轴表示迭代次数,纵轴表示适应度值。随着迭代次数的增加,适应度值迅速下降并趋于稳定,表明算法能够快速找到接近最优的解。

部分代码
% 初始化参数
num_particles = 50; % 粒子数量
max_iterations = 500; % 最大迭代次数
temperature = 100; % 初始温度
% 随机初始化路径点
positions = rand(num_particles, 2) * 10; % 生成10x10范围内的随机点
best_path = inf; % 最优路径初始化为无穷大
% 迭代优化过程
for iter = 1:max_iterations
temperature = temperature * 0.99; % 模拟雪消融,温度逐渐降低
for i = 1:num_particles
% 计算当前路径的成本
path_cost = calculatePathCost(positions(i, :));
% 判断是否需要更新最优路径
if path_cost < best_path
best_path = path_cost;
best_position = positions(i, :);
end
% 根据雪消融模型调整路径
positions(i, :) = positions(i, :) + temperature * randn(1, 2);
end
end
% 成本计算函数
function cost = calculatePathCost(position)
% 计算路径的长度或其他代价
cost = norm(position);
end
参考文献
❝
Dorigo, M., & Stützle, T. (2004). Ant Colony Optimization. MIT Press.
Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. Proceedings of ICNN'95 - International Conference on Neural Networks, 4, 1942-1948.
Mirjalili, S. (2015). The ant lion optimizer. Advances in Engineering Software, 83, 80-98.
(文章内容仅供参考,具体效果以图片为准)