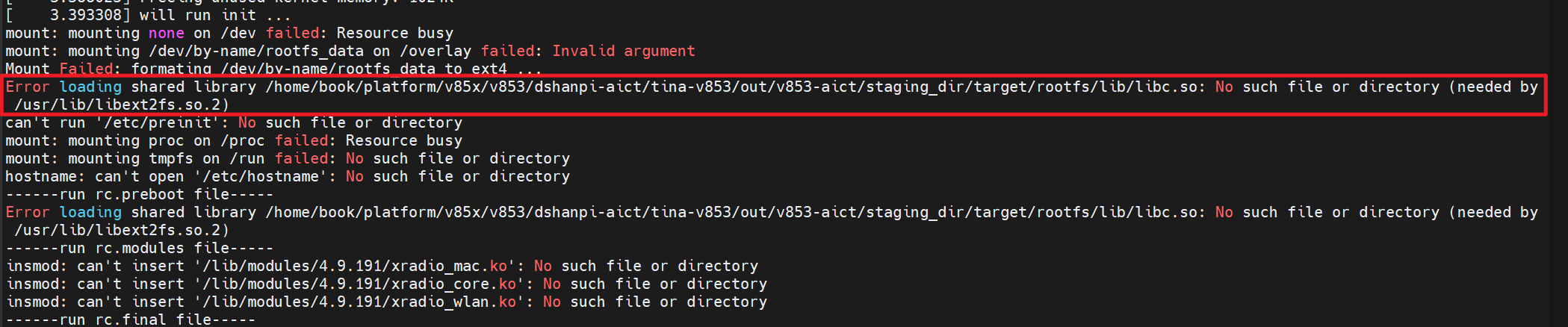
目录
- T1
- T2
- T3
- T4
- T5
- T6
T1
证明: E 3 E^3 E3中的正则曲线 r ( t ) (t) (t)的曲率和挠率分别是
κ
(
t
)
=
∣
r
′
(
t
)
∧
r
′
′
(
t
)
∣
∣
r
′
(
t
)
∣
3
\kappa(t)=\frac{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|}{|\mathbf{r}'(t)|^3}
κ(t)=∣r′(t)∣3∣r′(t)∧r′′(t)∣
τ
(
t
)
=
(
r
′
(
t
)
,
r
′
′
(
t
)
,
r
′
′
′
(
t
)
)
∣
r
′
(
t
)
∧
r
′
′
(
t
)
∣
2
\tau(t)=\frac{(\mathbf{r}'(t),\mathbf{r}''(t),\mathbf{r}'''(t))}{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|^2}
τ(t)=∣r′(t)∧r′′(t)∣2(r′(t),r′′(t),r′′′(t))
证明:设
s
s
s是曲线 r
(
t
)
(t)
(t)的弧长参数.则
s
=
s
(
t
)
s=s(t)
s=s(t)与
t
=
t
(
s
)
t=t(s)
t=t(s)互为反函数.由于空
间曲线的 Frenet 标架和曲率与(容许的)参数选取无关,故
t ( t ) : = t ( s ( t ) ) = d r ( t ( s ) ) d s = r ′ ( t ) d t d s , d t d s = 1 ∣ r ′ ( t ) ∣ t ˙ ( s ( t ) ) = r ′ ′ ( t ) ( d t d s ) 2 + r ′ ( t ) d 2 t d s 2 , n ( s ( t ) ) = 1 κ ( s ( t ) ) t ˙ ( s ( t ) ) , t ¨ ( s ( t ) ) = r ′ ′ ′ ( t ) ( d t d s ) 3 + 3 r ′ ′ ( t ) d t d s d 2 t d s 2 + r ′ ( t ) d 3 t d s 3 , b ( s ( t ) ) = t ( s ( t ) ) ∧ n ( s ( t ) ) = 1 κ ′ ′ ( s ( t ) ) t ( s ( t ) ) ∧ t ˙ ( s ( t ) ) = 1 κ ( s ( t ) ) r ′ ( t ) d t d s ∧ ( r ′ ′ ( t ) ( d t d s ) 2 + r ′ ( t ) d 2 t d s 2 ) = 1 κ ( s ( t ) ) ( d t d s ) 3 r ′ ( t ) ∧ r ′ ′ ( t ) \mathbf{t}(t):=\mathbf{t}(s(t))=\frac{d\mathbf{r}(t(s))}{ds}=\mathbf{r}'(t)\frac{dt}{ds},\quad\frac{dt}{ds}=\frac{1}{|\mathbf{r}'(t)|}\\ \dot{\mathbf{t}}(s(t))=\mathbf{r}^{\prime\prime}(t)(\frac{dt}{ds})^2+\mathbf{r}^{\prime}(t)\frac{d^2t}{ds^2},\quad\mathbf{n}(s(t))=\frac1{\kappa(s(t))}\dot{\mathbf{t}}(s(t)),\\\ddot{\mathbf{t}}(s(t))=\mathbf{r}^{\prime\prime\prime}(t)(\frac{dt}{ds})^3+3\mathbf{r}^{\prime\prime}(t)\frac{dt}{ds}\frac{d^2t}{ds^2}+\mathbf{r}^{\prime}(t)\frac{d^3t}{ds^3},\\\mathbf{b}(s(t))=\mathbf{t}(s(t))\wedge\mathbf{n}(s(t))=\frac1{\kappa^{\prime\prime}(s(t))}\mathbf{t}(s(t))\wedge\dot{\mathbf{t}}(s(t))\\=\frac1{\kappa(s(t))}\mathbf{r}'(t)\frac{dt}{ds}\wedge(\mathbf{r}''(t)(\frac{dt}{ds})^2+\mathbf{r}'(t)\frac{d^2t}{ds^2})\\=\frac1{\kappa(s(t))}(\frac{dt}{ds})^3\mathbf{r}'(t)\wedge\mathbf{r}''(t) t(t):=t(s(t))=dsdr(t(s))=r′(t)dsdt,dsdt=∣r′(t)∣1t˙(s(t))=r′′(t)(dsdt)2+r′(t)ds2d2t,n(s(t))=κ(s(t))1t˙(s(t)),t¨(s(t))=r′′′(t)(dsdt)3+3r′′(t)dsdtds2d2t+r′(t)ds3d3t,b(s(t))=t(s(t))∧n(s(t))=κ′′(s(t))1t(s(t))∧t˙(s(t))=κ(s(t))1r′(t)dsdt∧(r′′(t)(dsdt)2+r′(t)ds2d2t)=κ(s(t))1(dsdt)3r′(t)∧r′′(t)
从而,曲率
κ
(
t
)
=
κ
(
s
(
t
)
)
=
(
d
t
d
s
)
3
∣
r
′
(
t
)
∧
r
′
′
(
t
)
∣
=
∣
r
′
(
t
)
∧
r
′
′
(
t
)
∣
∣
r
′
(
t
)
∣
3
.
\kappa(t)=\kappa(s(t))=(\frac{dt}{ds})^3|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|=\frac{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|}{|\mathbf{r}'(t)|^3}.
κ(t)=κ(s(t))=(dsdt)3∣r′(t)∧r′′(t)∣=∣r′(t)∣3∣r′(t)∧r′′(t)∣.
由于
t
˙
(
s
)
=
κ
(
s
)
n
(
s
)
\dot{\mathbf{t}}(s)=\kappa(s)\mathbf{n}(s)
t˙(s)=κ(s)n(s),故
t
¨
(
s
)
=
κ
(
s
)
n
(
s
)
+
κ
(
s
)
n
˙
(
s
)
=
κ
˙
(
s
)
n
(
s
)
+
κ
(
s
)
(
−
κ
(
s
)
t
(
s
)
+
τ
(
s
)
b
(
s
)
)
\ddot{\mathbf{t}}(s)=\kappa(s)\mathbf{n}(s)+\kappa(s)\dot{\mathbf{n}}(s)=\dot{\kappa}(s)\mathbf{n}(s)+\kappa(s)(-\kappa(s)\mathbf{t}(s)+\tau(s)\mathbf{b}(s))
t¨(s)=κ(s)n(s)+κ(s)n˙(s)=κ˙(s)n(s)+κ(s)(−κ(s)t(s)+τ(s)b(s))
= − κ ( s ) 2 t ( s ) + κ ˙ ( s ) n ( s ) + κ ( s ) τ ( s ) b ( s ) . =-\kappa(s)^2\mathbf{t}(s)+\dot{\kappa}(s)\mathbf{n}(s)+\kappa(s)\tau(s)\mathbf{b}(s). =−κ(s)2t(s)+κ˙(s)n(s)+κ(s)τ(s)b(s).
从而,
κ
(
s
(
t
)
)
τ
(
s
(
t
)
)
=
⟨
t
¨
(
s
(
t
)
)
,
b
(
s
(
t
)
)
⟩
=
⟨
r
′
′
′
(
t
)
(
d
t
d
s
)
3
+
3
r
′
′
(
t
)
d
t
d
s
d
2
t
d
s
2
+
r
′
(
t
)
d
3
t
d
s
3
,
1
κ
(
s
(
t
)
)
t
(
s
(
t
)
)
∧
t
˙
(
s
(
t
)
)
⟩
=
1
κ
(
s
(
t
)
)
(
d
t
d
s
)
6
(
r
′
(
t
)
,
r
′
′
(
t
)
,
r
′
′
′
(
t
)
)
.
\begin{aligned} \kappa(s(t))\tau(s(t))&=\langle\ddot{\mathbf{t}}(s(t)),\mathbf{b}(s(t))\rangle\\ &=\langle\mathbf{r}^{\prime\prime\prime}(t)(\frac{dt}{ds})^3+3\mathbf{r}^{\prime\prime}(t)\frac{dt}{ds}\frac{d^2t}{ds^2}+\mathbf{r}^{\prime}(t)\frac{d^3t}{ds^3},\frac1{\kappa(s(t))}\mathbf{t}(s(t))\wedge\dot{\mathbf{t}}(s(t))\rangle\\&=\frac1{\kappa(s(t))}(\frac{dt}{ds})^6(\mathbf{r}^{\prime}(t),\mathbf{r}^{\prime\prime}(t),\mathbf{r}^{\prime\prime\prime}(t)).\end{aligned}
κ(s(t))τ(s(t))=⟨t¨(s(t)),b(s(t))⟩=⟨r′′′(t)(dsdt)3+3r′′(t)dsdtds2d2t+r′(t)ds3d3t,κ(s(t))1t(s(t))∧t˙(s(t))⟩=κ(s(t))1(dsdt)6(r′(t),r′′(t),r′′′(t)).
因此,
τ ( t ) = τ ( s ( t ) ) = 1 κ ( t ) 2 1 ∣ r ′ ( t ) ∣ 6 ( r ′ ( t ) , r ′ ′ ( t ) , r ′ ′ ′ ( t ) ) = ( r ′ ( t ) , r ′ ′ ( t ) , r ′ ′ ′ ( t ) ) ∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ 2 . \tau(t)=\tau(s(t))=\frac1{\kappa(t)^2}\frac1{|\mathbf{r}'(t)|^6}(\mathbf{r}'(t),\mathbf{r}''(t),\mathbf{r}'''(t))=\frac{(\mathbf{r}'(t),\mathbf{r}''(t),\mathbf{r}'''(t))}{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|^2}. τ(t)=τ(s(t))=κ(t)21∣r′(t)∣61(r′(t),r′′(t),r′′′(t))=∣r′(t)∧r′′(t)∣2(r′(t),r′′(t),r′′′(t)).
注:任意参数曲线 r ( t ) (t) (t)的 Frenet 标架为 { r ( t ) ; t ( t ) , n ( t ) , b ( t ) } \{\mathbf{r}(t);\mathbf{t}(t),\mathbf{n}(t),\mathbf{b}(t)\} {r(t);t(t),n(t),b(t)},其中
t ( t ) = r ′ ( t ) ∣ r ′ ( t ) ∣ = ( x ′ x ′ 2 + y ′ 2 + z ′ 2 , y ′ x ′ 2 + y ′ 2 + z ′ 2 , x ′ x ′ 2 + y ′ 2 + z ′ 2 ) \mathbf{t}(t)=\frac{\mathbf{r}'(t)}{|\mathbf{r}'(t)|}=(\frac{x'}{\sqrt{x'^2+y'^2+z'^2}},\frac{y'}{\sqrt{x'^2+y'^2+z'^2}},\frac{x'}{\sqrt{x'^2+y'^2+z'^2}}) t(t)=∣r′(t)∣r′(t)=(x′2+y′2+z′2x′,x′2+y′2+z′2y′,x′2+y′2+z′2x′)
n ( t ) = r ′ ′ ( t ) ∣ r ′ ′ ( t ) ∣ \mathbf{n}(t)=\frac{\mathbf{r}''(t)}{|\mathbf{r}''(t)|} n(t)=∣r′′(t)∣r′′(t)
b ( t ) = r ′ ( t ) ∧ r ′ ′ ( t ) ∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ \mathbf{b}(t)=\frac{\mathbf{r}'(t)\wedge\mathbf{r}''(t)}{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|} b(t)=∣r′(t)∧r′′(t)∣r′(t)∧r′′(t)
T2
求 下 列 曲 线 的 曲 率 和 挠 率 :
(
1
)
r
(
t
)
=
(
a
cosh
t
,
a
sinh
t
,
b
t
)
(
a
>
0
)
;
( 1) \textbf{ r}( t) = ( a\cosh t, a\sinh t, bt) ( a> 0) ;
(1) r(t)=(acosht,asinht,bt)(a>0);
(
2
)
r
(
t
)
=
(
3
t
−
t
2
,
3
t
2
,
3
t
+
t
2
)
;
( 2) \textbf{ r}( t) = ( 3t- t^2, 3t^2, 3t+ t^2) ;
(2) r(t)=(3t−t2,3t2,3t+t2);
(
3
)
r
(
t
)
=
(
a
(
1
−
sin
t
)
,
a
(
1
−
cos
t
)
,
b
t
)
(
a
>
0
)
;
( 3) \textbf{ r}( t) = ( a( 1- \sin t) , a( 1- \cos t) , bt) ( a> 0) ;
(3) r(t)=(a(1−sint),a(1−cost),bt)(a>0);
(
4
)
r
(
t
)
=
(
a
t
,
2
a
log
t
,
a
t
)
(
a
>
0
)
.
( 4) \textbf{ r}( t) = ( at, \sqrt {2}a\log t, \frac at) ( a> 0) .
(4) r(t)=(at,2alogt,ta)(a>0).
(1)直接计算,得
r
′
(
t
)
=
(
a
sinh
t
,
a
cosh
t
,
b
)
\mathbf{r}^\prime(t)=(a\sinh t,a\cosh t,b)
r′(t)=(asinht,acosht,b)
r ′ ′ ( t ) = ( a cosh t , a sinh t , 0 ) \mathbf{r}^{\prime\prime}(t)=(a\cosh t,a\sinh t,0) r′′(t)=(acosht,asinht,0)
r ′ ′ ′ ( t ) = ( a sinh t , a cosh t , 0 ) \mathbf{r}^{\prime\prime\prime}(t)=(a\sinh t,a\cosh t,0) r′′′(t)=(asinht,acosht,0)
从而,
∣ r ′ ( t ) ∣ = a 2 cosh 2 t + b 2 , |\mathbf{r}'(t)|=\sqrt{a^2\cosh2t+b^2}, ∣r′(t)∣=a2cosh2t+b2,
r ′ ( t ) ∧ r ′ ′ ( t ) = ( − a b sinh t , a b cosh t , − a 2 ) , \mathbf{r}^{\prime}(t)\wedge\mathbf{r}^{\prime\prime}(t)=(-ab\sinh t,ab\cosh t,-a^2), r′(t)∧r′′(t)=(−absinht,abcosht,−a2),
∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ = a b 2 cosh 2 t + a 2 , |\mathbf{r}^{\prime}(t)\wedge\mathbf{r}^{\prime\prime}(t)|=a\sqrt{b^{2}\cosh2t+a^{2}}, ∣r′(t)∧r′′(t)∣=ab2cosh2t+a2,
( r ′ ( t ) , r ′ ′ ( t ) , r ′ ′ ′ ′ ( t ) ) = ⟨ r ′ ( t ) ∧ r ′ ′ ( t ) , r ′ ′ ′ ′ ( t ) ⟩ = a 2 b . (\mathbf{r}'(t),\mathbf{r}''(t),\mathbf{r}''''(t))=\langle\mathbf{r}'(t)\wedge\mathbf{r}''(t),\mathbf{r}''''(t)\rangle=a^2b. (r′(t),r′′(t),r′′′′(t))=⟨r′(t)∧r′′(t),r′′′′(t)⟩=a2b.
故曲率
κ ( t ) = ∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ ∣ r ′ ( t ) ∣ 3 = a b 2 cosh 2 t + a 2 ( a 2 cosh 2 t + b 2 ) 3 2 , \kappa(t)=\frac{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|}{|\mathbf{r}'(t)|^3}=\frac{a\sqrt{b^2\cosh2t+a^2}}{(a^2\cosh2t+b^2)^{\frac32}}, κ(t)=∣r′(t)∣3∣r′(t)∧r′′(t)∣=(a2cosh2t+b2)23ab2cosh2t+a2,
挠率
τ ( t ) = ( r ′ ( t ) , r ′ ′ ( t ) , r ′ ′ ′ ( t ) ) ∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ 2 = b b 2 cosh 2 t + a 2 . \tau(t)=\frac{(\mathbf{r}'(t),\mathbf{r}''(t),\mathbf{r}'''(t))}{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|^2}=\frac{b}{b^2\cosh2t+a^2}. τ(t)=∣r′(t)∧r′′(t)∣2(r′(t),r′′(t),r′′′(t))=b2cosh2t+a2b.
T3
求 下 列 曲 线 的 曲 率 和 挠 率 :
(
1
)
r
(
t
)
=
(
a
cosh
t
,
a
sinh
t
,
b
t
)
(
a
>
0
)
;
( 1) \textbf{ r}( t) = ( a\cosh t, a\sinh t, bt) ( a> 0) ;
(1) r(t)=(acosht,asinht,bt)(a>0);
(
2
)
r
(
t
)
=
(
3
t
−
t
2
,
3
t
2
,
3
t
+
t
2
)
;
( 2) \textbf{ r}( t) = ( 3t- t^2, 3t^2, 3t+ t^2) ;
(2) r(t)=(3t−t2,3t2,3t+t2);
(
3
)
r
(
t
)
=
(
a
(
1
−
sin
t
)
,
a
(
1
−
cos
t
)
,
b
t
)
(
a
>
0
)
;
( 3) \textbf{ r}( t) = ( a( 1- \sin t) , a( 1- \cos t) , bt) ( a> 0) ;
(3) r(t)=(a(1−sint),a(1−cost),bt)(a>0);
(
4
)
r
(
t
)
=
(
a
t
,
2
a
log
t
,
a
t
)
(
a
>
0
)
.
( 4) \textbf{ r}( t) = ( at, \sqrt {2}a\log t, \frac at) ( a> 0) .
(4) r(t)=(at,2alogt,ta)(a>0).
(2)直接计算,得
r
′
(
t
)
=
(
3
−
2
t
,
6
t
,
3
+
2
t
)
,
\mathbf{r}'(t)=(3-2t,6t,3+2t),
r′(t)=(3−2t,6t,3+2t),
r
′
′
(
t
)
=
(
−
2
,
6
,
2
)
,
\mathbf{r}''(t)=(-2,6,2),
r′′(t)=(−2,6,2),
r
′
′
′
(
t
)
=
0
\mathbf{r}^{\prime\prime\prime}(t)=\mathbf{0}
r′′′(t)=0
从而,
∣
r
′
(
t
)
∣
=
2
(
4
t
2
+
18
t
+
9
)
|\mathbf{r}'(t)|=\sqrt{2(4t^2+18t+9)}
∣r′(t)∣=2(4t2+18t+9)
r
′
(
t
)
∧
r
′
′
(
t
)
=
(
−
18
,
−
12
,
18
)
\mathbf{r}'(t)\wedge\mathbf{r}''(t)=(-18,-12,18)
r′(t)∧r′′(t)=(−18,−12,18)
∣
r
′
(
t
)
∧
r
′
′
(
t
)
∣
=
6
22
|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|=6\sqrt{22}
∣r′(t)∧r′′(t)∣=622
(
r
′
(
t
)
,
r
′
′
(
t
)
,
r
′
′
′
(
t
)
)
=
0
(\mathbf{r}'(t),\mathbf{r}''(t),\mathbf{r}'''(t))=0
(r′(t),r′′(t),r′′′(t))=0
故曲率
κ ( t ) = ∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ ∣ r ′ ( t ) ∣ 3 = 3 11 ( 4 t 2 + 18 t + 9 ) 3 2 \kappa(t)=\frac{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|}{|\mathbf{r}'(t)|^3}=\frac{3\sqrt{11}}{(4t^2+18t+9)^{\frac32}} κ(t)=∣r′(t)∣3∣r′(t)∧r′′(t)∣=(4t2+18t+9)23311
挠率
τ ( t ) = ( r ′ ( t ) , r ′ ′ ( t ) , r ′ ′ ′ ( t ) ) ∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ 2 = 0. \tau(t)=\frac{(\mathbf{r}'(t),\mathbf{r}''(t),\mathbf{r}'''(t))}{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|^2}=0. τ(t)=∣r′(t)∧r′′(t)∣2(r′(t),r′′(t),r′′′(t))=0.
T4
求 下 列 曲 线 的 曲 率 和 挠 率 :
(
1
)
r
(
t
)
=
(
a
cosh
t
,
a
sinh
t
,
b
t
)
(
a
>
0
)
;
( 1) \textbf{ r}( t) = ( a\cosh t, a\sinh t, bt) ( a> 0) ;
(1) r(t)=(acosht,asinht,bt)(a>0);
(
2
)
r
(
t
)
=
(
3
t
−
t
2
,
3
t
2
,
3
t
+
t
2
)
;
( 2) \textbf{ r}( t) = ( 3t- t^2, 3t^2, 3t+ t^2) ;
(2) r(t)=(3t−t2,3t2,3t+t2);
(
3
)
r
(
t
)
=
(
a
(
1
−
sin
t
)
,
a
(
1
−
cos
t
)
,
b
t
)
(
a
>
0
)
;
( 3) \textbf{ r}( t) = ( a( 1- \sin t) , a( 1- \cos t) , bt) ( a> 0) ;
(3) r(t)=(a(1−sint),a(1−cost),bt)(a>0);
(
4
)
r
(
t
)
=
(
a
t
,
2
a
log
t
,
a
t
)
(
a
>
0
)
.
( 4) \textbf{ r}( t) = ( at, \sqrt {2}a\log t, \frac at) ( a> 0) .
(4) r(t)=(at,2alogt,ta)(a>0).
(3)直接计算,得
r ′ ( t ) = ( − a cos t , a sin t , b ) , r ′ ′ ( t ) = ( a sin t , a cos t , 0 ) , r ′ ′ ′ ( t ) = ( a cos t , − a sin t , 0 ) . \mathbf{r}'(t)=(-a\cos t,a\sin t,b),\\\mathbf{r}''(t)=(a\sin t,a\cos t,0),\\\mathbf{r}'''(t)=(a\cos t,-a\sin t,0). r′(t)=(−acost,asint,b),r′′(t)=(asint,acost,0),r′′′(t)=(acost,−asint,0).
从而,
∣ r ′ ( t ) ∣ = a 2 + b 2 , |\mathbf{r}'(t)|=\sqrt{a^2+b^2}, ∣r′(t)∣=a2+b2,
r
′
(
t
)
∧
r
′
′
(
t
)
=
(
−
a
b
cos
t
,
a
b
sin
t
,
−
a
2
)
\mathbf{r}^{\prime}(t)\wedge\mathbf{r}^{\prime\prime}(t)=(-ab\cos t,ab\sin t,-a^{2})
r′(t)∧r′′(t)=(−abcost,absint,−a2)
∣
r
′
(
t
)
∧
r
′
′
(
t
)
∣
=
a
a
2
+
b
2
,
|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|=a\sqrt{a^2+b^2},
∣r′(t)∧r′′(t)∣=aa2+b2,
(
r
′
(
t
)
,
r
′
′
(
t
)
,
r
′
′
′
(
t
)
)
=
⟨
r
′
(
t
)
∧
r
′
′
(
t
)
,
r
′
′
′
′
(
t
)
⟩
=
−
a
2
b
.
(\mathbf{r}'(t),\mathbf{r}''(t),\mathbf{r}'''(t))=\langle\mathbf{r}'(t)\wedge\mathbf{r}''(t),\mathbf{r}''''(t)\rangle=-a^2b.
(r′(t),r′′(t),r′′′(t))=⟨r′(t)∧r′′(t),r′′′′(t)⟩=−a2b.
故曲率
κ ( t ) = ∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ ∣ r ′ ( t ) ∣ 3 = a a 2 + b 2 ( a 2 + b 2 ) 3 2 = a a 2 + b 2 , \kappa(t)=\frac{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|}{|\mathbf{r}'(t)|^3}=\frac{a\sqrt{a^2+b^2}}{(a^2+b^2)^{\frac32}}=\frac{a}{a^2+b^2}, κ(t)=∣r′(t)∣3∣r′(t)∧r′′(t)∣=(a2+b2)23aa2+b2=a2+b2a,
挠率
τ ( t ) = ( r ′ ( t ) , r ′ ′ ( t ) , r ′ ′ ′ ( t ) ) ∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ 2 = − a 2 b a 2 ( a 2 + b 2 ) = − b a 2 + b 2 . \tau(t)=\frac{(\mathbf{r}'(t),\mathbf{r}''(t),\mathbf{r}'''(t))}{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|^2}=\frac{-a^2b}{a^2(a^2+b^2)}=-\frac b{a^2+b^2}. τ(t)=∣r′(t)∧r′′(t)∣2(r′(t),r′′(t),r′′′(t))=a2(a2+b2)−a2b=−a2+b2b.
T5
求 下 列 曲 线 的 曲 率 和 挠 率 :
(
1
)
r
(
t
)
=
(
a
cosh
t
,
a
sinh
t
,
b
t
)
(
a
>
0
)
;
( 1) \textbf{ r}( t) = ( a\cosh t, a\sinh t, bt) ( a> 0) ;
(1) r(t)=(acosht,asinht,bt)(a>0);
(
2
)
r
(
t
)
=
(
3
t
−
t
2
,
3
t
2
,
3
t
+
t
2
)
;
( 2) \textbf{ r}( t) = ( 3t- t^2, 3t^2, 3t+ t^2) ;
(2) r(t)=(3t−t2,3t2,3t+t2);
(
3
)
r
(
t
)
=
(
a
(
1
−
sin
t
)
,
a
(
1
−
cos
t
)
,
b
t
)
(
a
>
0
)
;
( 3) \textbf{ r}( t) = ( a( 1- \sin t) , a( 1- \cos t) , bt) ( a> 0) ;
(3) r(t)=(a(1−sint),a(1−cost),bt)(a>0);
(
4
)
r
(
t
)
=
(
a
t
,
2
a
log
t
,
a
t
)
(
a
>
0
)
.
( 4) \textbf{ r}( t) = ( at, \sqrt {2}a\log t, \frac at) ( a> 0) .
(4) r(t)=(at,2alogt,ta)(a>0).
(4)注意到 t ∈ ( 0 , + ∞ ) . t\in(0,+\infty). t∈(0,+∞). 直接计算,得
r ′ ( t ) = ( a , 2 a t , − a t 2 ) , \mathbf{r}'(t)=(a,\frac{\sqrt{2}a}t,-\frac a{t^2}), r′(t)=(a,t2a,−t2a),
r ′ ′ ( t ) = ( 0 , − 2 a t 2 , 2 a t 3 ) , \mathbf{r}^{\prime\prime}(t)=(0,-\frac{\sqrt{2}a}{t^2},\frac{2a} {t^3}), r′′(t)=(0,−t22a,t32a),
r ′ ′ ′ ( t ) = ( 0 , 2 2 a t 3 , − 6 a t 4 ) . \mathbf{r}^{\prime\prime\prime}(t)=(0,\frac{2\sqrt{2}a}{t^3},-\frac{6a}{t^4}). r′′′(t)=(0,t322a,−t46a).
从而,
∣ r ′ ( t ) ∣ = a ( t 2 + 1 ) t 2 , |\mathbf{r}'(t)|=\frac{a(t^2+1)}{t^2}, ∣r′(t)∣=t2a(t2+1),
r ′ ( t ) ∧ r ′ ′ ( t ) = ( 2 a 2 t 4 , − 2 a 2 t 3 , − 2 a 2 t 2 ) , \mathbf{r}^{\prime}(t)\wedge\mathbf{r}^{\prime\prime}(t)=(\frac{\sqrt2a^2}{t^4},-\frac{2a^2}{t^3},-\frac{\sqrt2a^2}{t^2}), r′(t)∧r′′(t)=(t42a2,−t32a2,−t22a2),
∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ = 2 a 2 ( t 2 + 1 ) t 4 , |\mathbf{r}'(t)\wedge\mathbf{r}''(t)|=\frac{\sqrt{2}a^2(t^2+1)}{t^4}, ∣r′(t)∧r′′(t)∣=t42a2(t2+1),
( r ′ ( t ) , r ′ ′ ( t ) , r ′ ′ ′ ( t ) ) = ⟨ r ′ ( t ) ∧ r ′ ′ ( t ) , r ′ ′ ′ ′ ( t ) ⟩ = 2 2 a 3 t 6 . (\mathbf{r}'(t),\mathbf{r}''(t),\mathbf{r}'''(t))=\langle\mathbf{r}'(t)\wedge\mathbf{r}''(t),\mathbf{r}''''(t)\rangle=\frac{2\sqrt{2}a^3}{t^6}. (r′(t),r′′(t),r′′′(t))=⟨r′(t)∧r′′(t),r′′′′(t)⟩=t622a3.
故曲率
κ ( t ) = ∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ ∣ r ′ ( t ) ∣ 3 = 2 t 2 a ( t 2 + 1 ) 2 , \kappa(t)=\frac{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|}{|\mathbf{r}'(t)|^3}=\frac{\sqrt{2}t^2}{a(t^2+1)^2}, κ(t)=∣r′(t)∣3∣r′(t)∧r′′(t)∣=a(t2+1)22t2,
挠率
τ ( t ) = ( r ′ ( t ) , r ′ ′ ( t ) , r ′ ′ ′ ( t ) ) ∣ r ′ ( t ) ∧ r ′ ′ ( t ) ∣ 2 = 2 t 2 a ( t 2 + 1 ) 2 . \tau(t)=\frac{(\mathbf{r}'(t),\mathbf{r}''(t),\mathbf{r}'''(t))}{|\mathbf{r}'(t)\wedge\mathbf{r}''(t)|^2}=\frac{\sqrt{2}t^2}{a(t^2+1)^2}. τ(t)=∣r′(t)∧r′′(t)∣2(r′(t),r′′(t),r′′′(t))=a(t2+1)22t2.
T6
证明:曲线
r
(
s
)
=
(
(
1
+
s
)
3
2
3
,
(
1
−
s
)
3
2
3
,
s
2
)
(
−
1
<
s
<
1
)
\mathbf{r}(s)=(\frac{(1+s)^\frac{3}{2}}{3},\frac{(1-s)^\frac{3}{2}}{3},\frac{s}{\sqrt{2}})\:(-1<s<1)
r(s)=(3(1+s)23,3(1−s)23,2s)(−1<s<1)
以
s
s
s为弧长参数,并求它的曲率、挠率和 Frenet 标架。
证明:由于
r
′
(
s
)
=
(
(
1
+
s
)
1
s
2
,
−
(
1
−
s
)
1
s
2
,
1
2
)
(
−
1
<
s
<
1
)
,
\mathbf{r}'(s)=(\frac{(1+s)^{\frac1s}}2,-\frac{(1-s)^{\frac1s}}2,\frac1{\sqrt2})\:(-1<s<1),
r′(s)=(2(1+s)s1,−2(1−s)s1,21)(−1<s<1),
∣
r
′
(
s
)
∣
=
1
+
s
4
+
1
−
s
4
+
1
2
=
1.
|\mathbf{r}^{\prime}(s)|=\sqrt{\frac{1+s}4+\frac{1-s}4+\frac12}=1.
∣r′(s)∣=41+s+41−s+21=1.
故
s
s
s是弧长参数.从而,
t
(
s
)
=
r
′
(
s
)
,
\mathbf{t}(s)=\mathbf{r}'(s),
t(s)=r′(s),
t
˙
(
s
)
=
(
(
1
+
s
)
−
1
2
4
,
−
(
1
−
s
)
−
1
2
4
,
0
)
.
\dot{\mathbf{t}}(s)=(\frac{(1+s)^{-\frac12}}4,-\frac{(1-s)^{-\frac12}}4,0).
t˙(s)=(4(1+s)−21,−4(1−s)−21,0).
故曲率
κ
(
s
)
=
∣
t
˙
(
s
)
∣
=
1
8
(
1
−
s
2
)
=
2
(
1
−
s
2
)
−
1
2
4
.
\kappa(s)=|\dot{\mathbf{t}}(s)|=\sqrt\frac1{8(1-s^2)}=\frac{\sqrt{2}(1-s^2)^{-\frac12}}4.
κ(s)=∣t˙(s)∣=8(1−s2)1=42(1−s2)−21.
从而
n
(
s
)
=
1
κ
t
˙
(
s
)
=
(
2
(
1
−
s
)
1
2
2
,
2
(
1
+
s
)
1
2
2
,
0
)
,
\mathbf{n}(s)=\frac1\kappa\dot{\mathbf{t}}(s)=(\frac{\sqrt2(1-s)^{\frac12}}2,\frac{\sqrt2(1+s)^{\frac12}}2,0),
n(s)=κ1t˙(s)=(22(1−s)21,22(1+s)21,0),
n
˙
(
s
)
=
(
−
2
(
1
−
s
)
−
1
2
4
,
2
(
1
+
s
)
−
1
2
4
,
0
)
,
\dot{\mathbf{n}}(s)=(-\frac{\sqrt{2}(1-s)^{-\frac{1}{2}}}4,\frac{\sqrt{2}(1+s)^{-\frac{1}{2}}}4,0),
n˙(s)=(−42(1−s)−21,42(1+s)−21,0),
b
(
s
)
=
t
(
s
)
∧
n
(
s
)
=
(
−
(
1
+
s
)
1
2
2
,
(
1
−
s
)
1
2
2
,
2
2
)
.
\mathbf{b}(s)=\mathbf{t}(s)\wedge\mathbf{n}(s)=(-\frac{(1+s)^{\frac12}}2,\frac{(1-s)^{\frac12}}2,\frac{\sqrt{2}}2).
b(s)=t(s)∧n(s)=(−2(1+s)21,2(1−s)21,22).
挠率
τ
(
s
)
=
⟨
n
˙
(
s
)
,
b
(
s
)
⟩
(
=
−
⟨
b
˙
(
s
)
,
n
(
s
)
⟩
)
=
2
(
1
−
s
2
)
−
1
2
4
.
\tau(s)=\langle\dot{\mathbf{n}}(s),\mathbf{b}(s)\rangle(=-\langle\dot{\mathbf{b}}(s),\mathbf{n}(s)\rangle)=\frac{\sqrt{2}(1-s^2)^{-\frac12}}4.
τ(s)=⟨n˙(s),b(s)⟩(=−⟨b˙(s),n(s)⟩)=42(1−s2)−21.
最后,曲线
r
(
s
)
\mathbf{r}(s)
r(s)的 Frenet 标架为
{
r
(
s
)
;
t
(
s
)
,
n
(
s
)
,
b
(
s
)
}
\{\mathbf{r}(s);\mathbf{t}(s),\mathbf{n}(s),\mathbf{b}(s)\}
{r(s);t(s),n(s),b(s)},其中
t
,
n
,
b
\mathbf{t},\mathbf{n},\mathbf{b}
t,n,b如上










![[PHP]Undefined index错误只针对数组](https://i-blog.csdnimg.cn/direct/71d1ed2906c6465f90d6ceb7dd09b5f2.png)