AntColonyOptimization蚁群算法
智能算法是路线规划、深度学习等等一系列领域所使用的优化算法,是算法进阶之路的必备之路。前言:本文主要围绕解决TSP旅行商问题展开,对于机器人的路线规划以及非线性方程求解的问题等解决方案
对于一些其他优化算法例如遗传算法解决一些现实问题都有实现!!
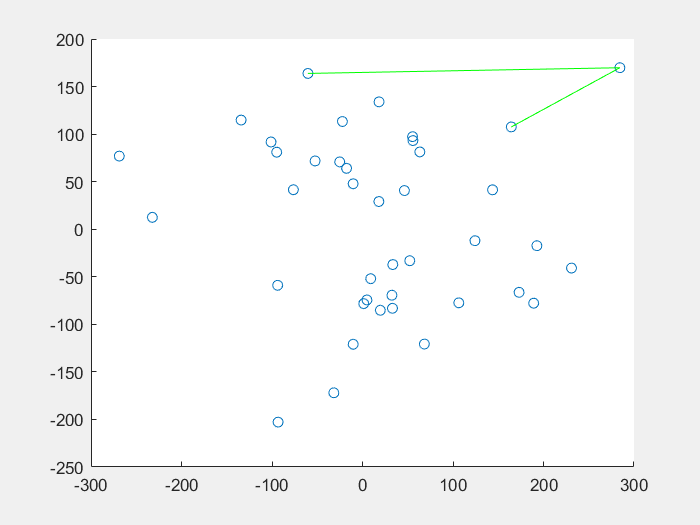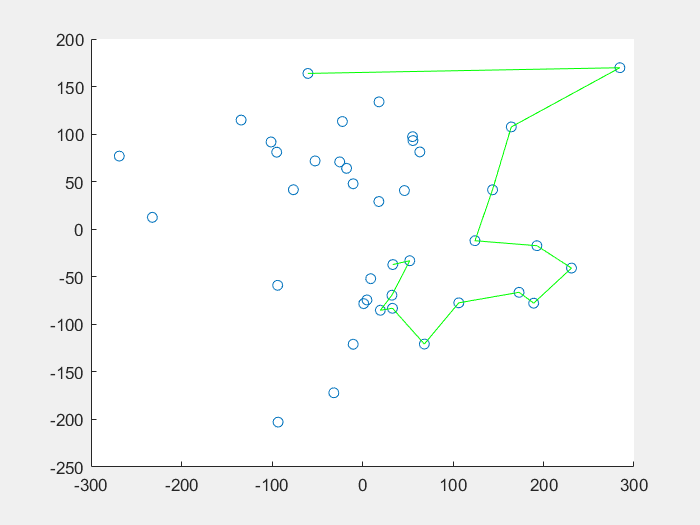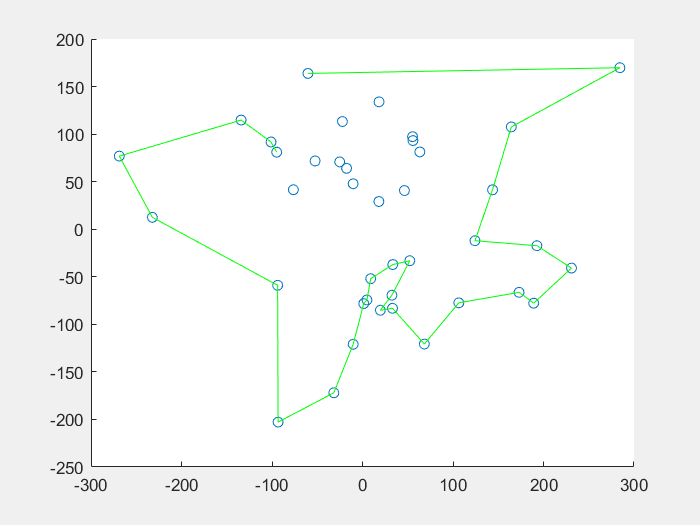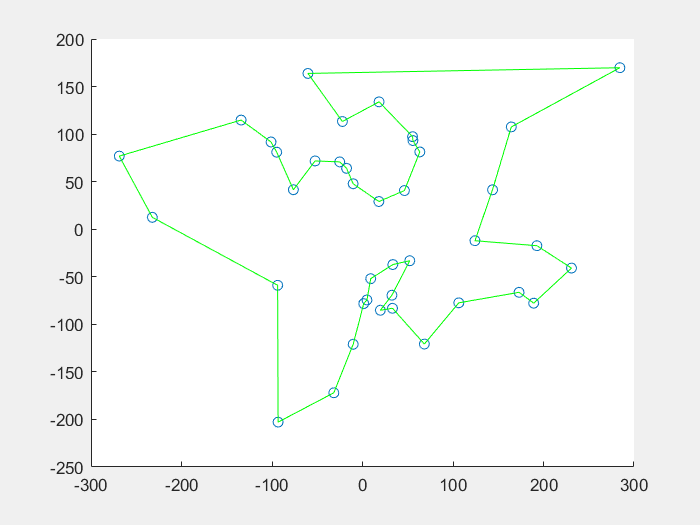
先看一下效果图:
蚁群算法解决TSP问题:
蚁群算法解决机器人路径规划问题:
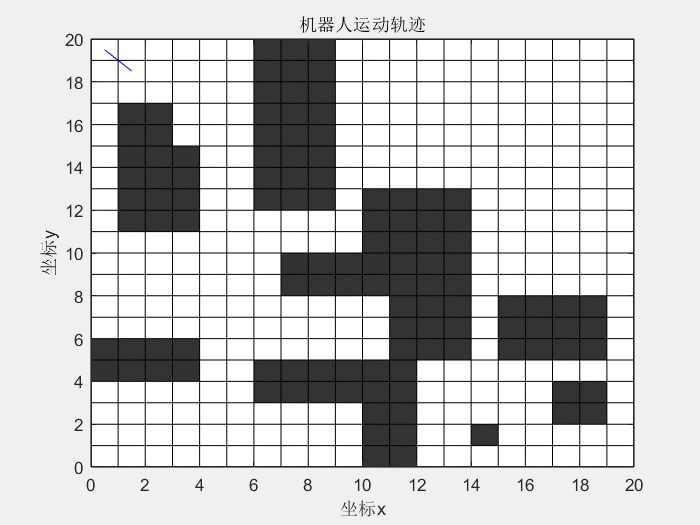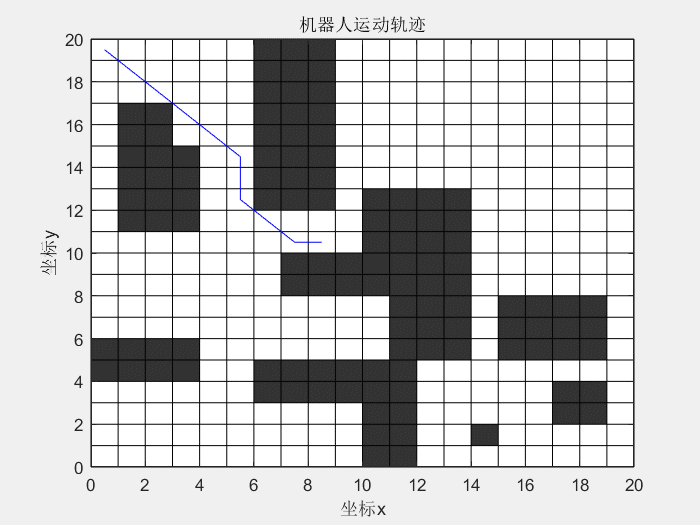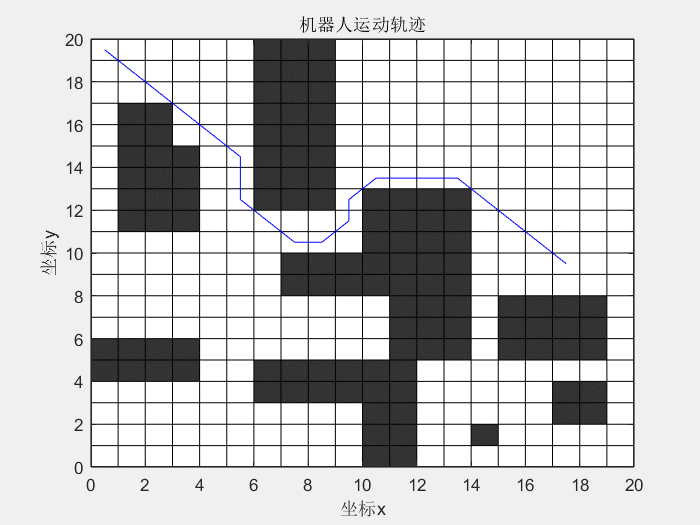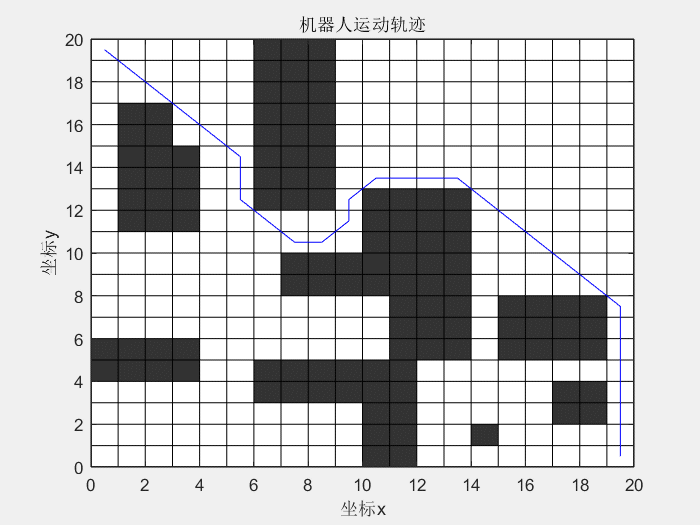
1、什么是蚁群算法
1.1、蚁群算法的来源
同遗传算法相似,都来自于大自然的启迪。蚁群算法就来自于蚂蚁寻找食物过程中发现路径的行为。
蚂蚁并没有视觉却可以寻找到食物,这得益于蚂蚁分泌的信息素,蚂蚁之间相互独立,彼此之间通过信息素进行交流,从而实现群体行为。
1.2、蚁群算法的基本原理
基本原理的过程就是蚂蚁觅食的过程。首先,蚂蚁在觅食的过程中会在路径上留下信息素的物质,并在寻找食物的过程中感知这种物质的强度,并指导自己的行为方向,他们总会朝着浓度高的方向前进。因此可以看得出来,蚂蚁觅食的过程是一个正反馈的过程,该路段经过的蚂蚁越多,信息素留下的就越多,浓度越高,更多的蚂蚁都会选择这个路段。
2、蚁群算法的实现原理
2.1、蚁群算法实现的重要规则(细品)
1. 避障规则
如果蚂蚁要移动的方向有障碍物挡住,他会随机的选择另外一个方向,如果有信息素指引的话,会按照信息素的指引前进。
2. 散播信息素规则
每只蚂蚁在刚找到食物的时候散发出来的信息素最多,并随着走选的距离,散播的信息越少。
3. 范围
蚂蚁观察的范围有限,只能在局部的范围内进行选择。例如蚂蚁观察的范围为3*3,那么它能够移动的范围也就是在这个3*3区域内。
4. 移动规则
前面也说过,蚂蚁的前进方向的选择依赖于信息素的浓度,回朝向信息素高的方向移动。当周围没有信息素或者信息素相同的时候,那么蚂蚁就会按照原来的方向继续前进,并且在前进方向上受到一个随机的扰动,为了避免再原地转圈,他会记住之前经过的点,下一次遇到的时候就会避开这个已经经过的点。
5. 觅食规则
如果蚂蚁在感知范围内找到食物则直接过去,加速模型的收敛,否则朝着信息素高的方向前进,并且每只蚂蚁都有小概率的犯错误,从而不是信息素最多的点移动,打破局部最优解的情况。
6. 环境
每只蚂蚁之间相互独立,他们依赖环境中的信息素进行交流。每只蚂蚁都仅仅能感知到环境内的信息。并且随机信息素会随着时间逐渐减少。如果这条路上经过的蚂蚁越来越少,那么信息素也会越来越少。
2.2、蚁群算法解决TSP问题的过程
旅行商问题(Traveling saleman problem, TSP)是物流配送的典型问题,他的求解有十分重要的理论和现实意义。
旅行商问题传统的解决方法都是遗传算法,但是遗传算法的收敛速度慢,具有一定的缺陷。
在求解TSP蚁群算法中,每只蚂蚁相互独立,用于构造不同的路线,蚂蚁之间通过信息素进行交流,合作求解。
基本过程如下:
- 初始化,设置迭代次数;
- 将 ants 只蚂蚁放置到 cities 个城市上;
- ants只蚂蚁按照概率函数选择下一个城市,并完成所有城市的周游;
- 记录本次迭代的最优路线;
- 全局更新信息素。
- 终止。本例终止条件是迭代次数,也可以设置运行时间或最短路径的下限。
- 输出结果
应用全局更新信息素来改变路径上信息素的值。当ants蚂蚁生成了ants个解,其中最短路径的是本代最优解,将属于这条路线上的所有关联的路线进行信息素更新。
之所以使用全局信息素,是为了让最优路径上有格外的信息素支持,这样后面的蚂蚁会优先选择这条路线。并且伴随着信息素的挥发,全局最短路径关联路线信息素得到进一步增强。
3、蚁群算法TSP程序实现
3.1、程序中矩阵大小以及含义
程序中矩阵说明(首字母大写):
| 矩阵 | 大小 | 含义 |
|---|---|---|
| Distance | (城市数量,城市数量) | 表征各个城市之间的距离信息 |
| Eta | (城市数量,城市数量) | 表征各个城市之间的启发因子 |
| Tau | (城市数量,城市数量) | 表征各个城市之间信息素的值 |
| Route | (蚂蚁个数,城市数量) | 每只蚂蚁周游城市的记录矩阵 |
| R_best | (迭代次数,城市数量) | 每次迭代的最优路线 |
| L_best | (迭代次数,1) | 每次迭代的最短距离 |
| L_ave | (迭代次数,1) | 每次迭代的平均距离 |
3.2、整体架构
'3.3、初始化变量参数'
'3.4、初始化矩阵参数'
while '迭代次数'
'3.5、安排蚂蚁初始位置'
'3.6、蚂蚁周游'
'3.7、记录最优路线以及最短距离'
'3.8、更新信息素'
end
'3.9、结果输出'
3.3、初始化变量参数
初始化主要对程序当中重要参数进行声明。
程序实现:
% 随机产生40个城市的坐标
position = 50 * randn(40, 2);
epochs = 50; % 迭代次数
% 蚂蚁个数最好大于等于城市个数,保证每个城市都有一个蚂蚁
ants = 40;
alpha = 1.4; % 表征信息素重要程度参数
beta = 2.2; % 表征启发因子重要程度参数
rho = 0.15; % 信息素挥发参数
Q = 10^6; % 信息素增强系数
cities = size(position, 1); % 城市个数
3.4、初始化矩阵参数
主要实现了重要矩阵声明以及初始化。
程序实现:
% 城市之间的距离矩阵
Distance = ones(cities, cities);
for i = 1: cities
for j = 1: cities
if i ~= j
% 坐标点欧氏距离
Distance(i, j) = ((position(i, 1) - position(j, 1))^2 + (position(i, 2) - position(j, 2))^2)^0.5;
else
% 因为后面要取倒数,所以取一个浮点数精度大小
Distance(i, j) = eps;
end
Distance(j, i) = Distance(i, j);
end
end
% 启发因子矩阵
Eta = 1./Distance;
% 信息素初始值每个路线均相同为 1
Tau = ones(cities, cities);
% 每只蚂蚁的路线图
Route = zeros(ants, cities);
epoch = 1;
% 记录每回合最优城市
R_best = zeros(epochs, cities);
% 记录每回合最短距离
L_best = inf .* ones(epochs, 1);
% 记录每回合平均距离
L_ave = zeros(epochs, 1);
3.5、安排蚂蚁初始位置
主要是将所有的蚂蚁安置在所有的城市当中,蚂蚁个数 >= 城市个数。并且保证均匀分布。
% 初始随机位置
RandPos = [];
for i = 1: ceil(ants / cities)
RandPos = [RandPos, randperm(cities)];
end
% 初始位置转置就对应了Route矩阵中每只蚂蚁的初始位置
Route(:, 1) = (RandPos(1, 1:ants))';
3.6、蚂蚁周游
由于蚂蚁的初始位置已经确定,所有主要就是周游剩余的所有城市,循环(cities-1)次。里面的循环就是将所有的蚂蚁进行周游一次。
对于每只蚂蚁的周游主要是对剩余的城市进行周游,不能重复拜访同一个城市。NoVisited矩阵存储着该蚂蚁未访问的城市。然后在所有没有访问过城市中选择一个。选择的方式也是类似于轮盘赌法。概率函数表征信息素和启发因子,两者有着不同的重要程度。
P
=
[
τ
i
j
(
t
)
]
α
⋅
[
η
i
j
]
β
P = [\tau_{ij}(t)]^\alpha · [\eta_{ij}]^\beta
P=[τij(t)]α⋅[ηij]β
其中
τ
i
j
(
t
)
\tau_{ij}(t)
τij(t)为路线上
(
i
,
j
)
(i, j)
(i,j)上的信息素浓度;
η
i
j
\eta_{ij}
ηij为路线上
(
i
,
j
)
(i, j)
(i,j)上的启发式信息;
程序实现:
for j = 2: cities
for i = 1: ants
Visited = Route(i, 1:j-1);
NoVisited = zeros(1, (cities - j + 1));
P = NoVisited;
num = 1;
for k = 1: cities
if length(find(Visited == k)) == 0
NoVisited(num) = k;
num = num + 1;
end
end
for k = 1: length(NoVisited)
P(k) = (Tau(Visited(end), NoVisited(k))^alpha) * (Eta(Visited(end), NoVisited(k))^beta);
end
P = P / sum(P);
Pcum = cumsum(P);
select = find(Pcum >= rand);
to_visit = NoVisited(select(1));
Route(i, j) = to_visit;
end
end
3.7、记录最优路线以及最短距离
计算每个回合每只蚂蚁走过的距离。并记录该回合最短路径,最短距离和平均距离。
Distance_epoch = zeros(ants, 1);
for i = 1: ants
R = Route(i, :);
for j = 1: cities - 1
Distance_epoch(i) = Distance_epoch(i) + Distance(R(j), R(j + 1));
end
Distance_epoch(i) = Distance_epoch(i) + Distance(R(1), R(cities));
end
L_best(epoch) = min(Distance_epoch);
pos = find(Distance_epoch == L_best(epoch));
R_best(epoch, :) = Route(pos(1), :);
L_ave(epoch) = mean(Distance_epoch);
epoch = epoch + 1;
3.8、更新信息素
更新信息素主要保证获得最优距离的那条路线的信息素得到最大的增强。
Delta_Tau = zeros(cities, cities);
for i = 1: ants
for j = 1: (cities - 1)
Delta_Tau(Route(i, j), Route(i, j + 1)) = Delta_Tau(Route(i, j), Route(i, j + 1)) + Q / Distance_epoch(i);
end
Delta_Tau(Route(i, 1), Route(i, cities)) = Delta_Tau(Route(i, 1), Route(i, cities)) + Q / Distance_epoch(i);
end
Tau = (1 - rho) .* Tau + Delta_Tau;
Route = zeros(ants, cities);
3.9、结果输出
迭代完成后,在R_best矩阵中得到最短路径的最小路线,最后输出最优的结果。
结果输出实现:
Pos = find(L_best == min(L_best));
Short_Route = R_best(Pos(1), :);
Short_Length = L_best(Pos(1), :);
figure
subplot(121);
DrawRoute(position, Short_Route);
subplot(122);
plot(L_best);
hold on
plot(L_ave, 'r');
title('平均距离和最短距离');
画图函数实现:
function DrawRoute(C, R)
N = length(R);
scatter(C(:, 1), C(:, 2));
hold on
plot([C(R(1), 1), C(R(N), 1)], [C(R(1), 2), C(R(N), 2)], 'g');
hold on
for ii = 2: N
plot([C(R(ii - 1), 1), C(R(ii), 1)], [C(R(ii - 1), 2), C(R(ii), 2)], 'g');
hold on
end
title('旅行商规划');
4、结果
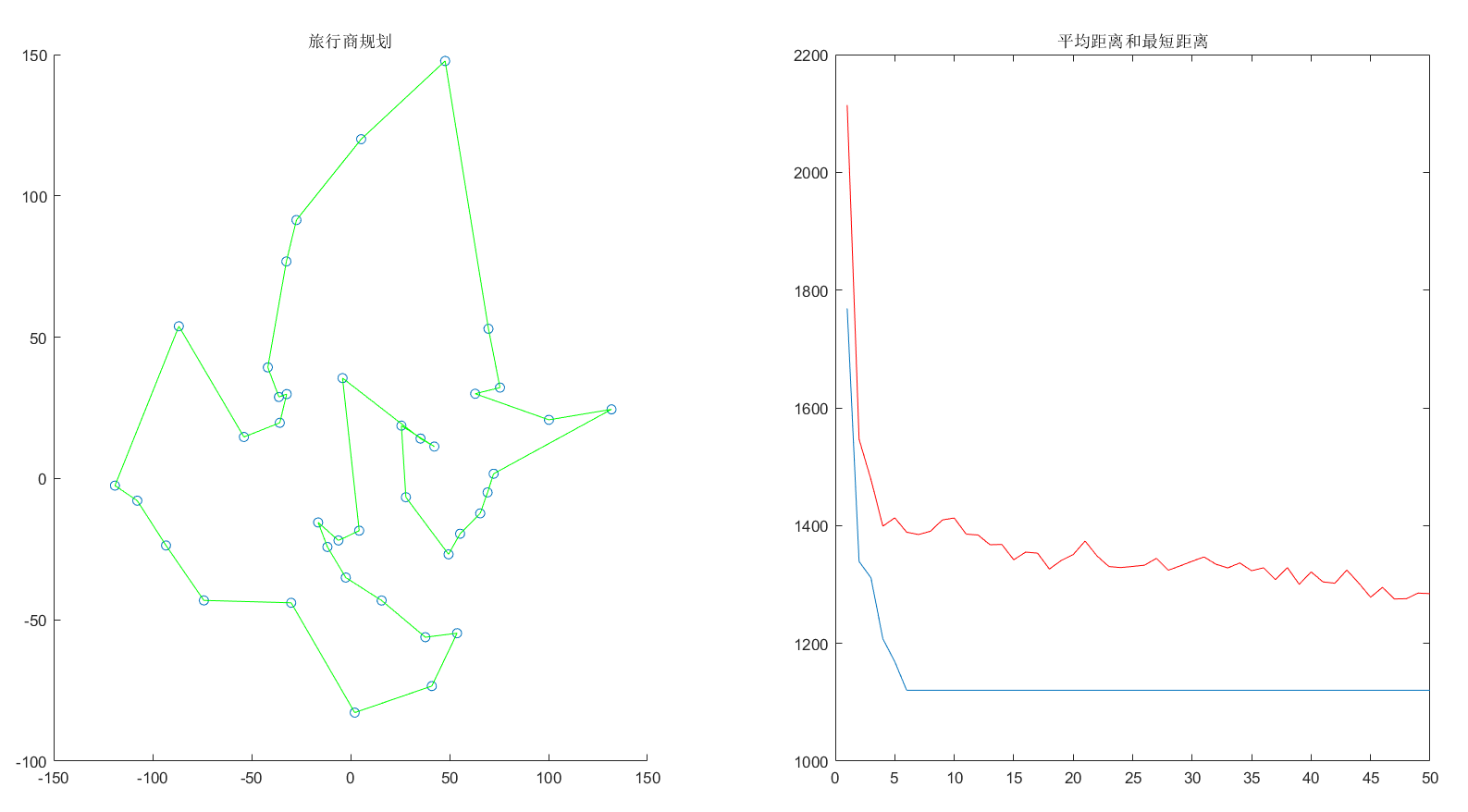
最后
学习到的小伙伴,请不要吝啬自己的点赞机会哦,主页资源有更多的学习资料,谢谢支持。