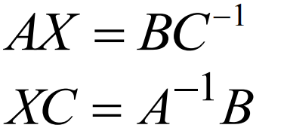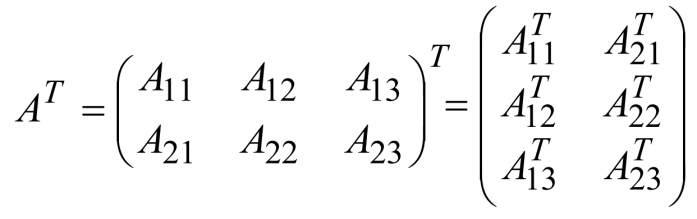目录
1.9 初等矩阵
1.9.1 初等矩阵的定义
1.9.2 初等矩阵的性质
1.9.3 初等矩阵与初等变换的关系
1.9.4 满秩矩阵的四种等价表述
1.10 逆矩阵的定义及可逆条件
1.10.1 逆矩阵的定义
1.10.2 矩阵可逆的条件
1.10.3 二阶可逆矩阵的逆矩阵求法
1.11 逆矩阵的求法(一)
1.11.1 逆矩阵的性质
1.11.2 初等变换法求逆矩阵
1.12 逆矩阵的求法(二)
1.12.1 定义法求逆矩阵
1.12.2 用定义证明B为A的逆
1.13 分块矩阵
1.13.1 分块矩阵的概念
1.13.2 分块矩阵的运算
1.13.3 准对角阵
1.13.4 分块三角阵
1.13.5 分块斜对角阵
1.14 矩阵方程
1.14.1 AX=B
1.14.2 XA=B
1.14.3 AXC=B
1.9 初等矩阵
1.9.1 初等矩阵的定义
对单位阵进行一次初等变换后得到的矩阵称为初等矩阵


1.9.2 初等矩阵的性质

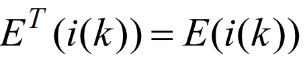

- 初等矩阵的转置仍为同类型的初等矩阵
- 初等矩阵都是非奇异的
- 初等矩阵的逆阵仍为同类型的初等矩阵
1.9.3 初等矩阵与初等变换的关系
行变换相当于左乘初等矩阵;
列变换相当于右乘初等矩阵
1.9.4 满秩矩阵的四种等价表述
以下命题等价
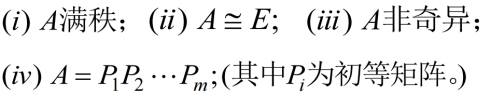
推论1
矩阵A与B等价的充要条件为存在m阶及n阶满秩阵P、Q,使得
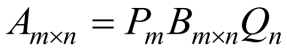
推论2
若P、Q为满秩阵,则
![]()
1.10 逆矩阵的定义及可逆条件
1.10.1 逆矩阵的定义
对n阶方阵A,若有n阶矩阵B,使AB=BA=E,
则称B为A的逆矩阵,称A为可逆的,记为
![]()
如果一个矩阵存在逆矩阵,那么其是惟一的。设B,C都是A的逆,则
B=EB=(CA)B =C(AB) =CE=C
并非每个方阵都可逆
1.10.2 矩阵可逆的条件
n阶方阵A可逆的充要条件是|A|≠0
A可逆⇔ A非奇异⇔A满秩
1.10.3 二阶可逆矩阵的逆矩阵求法

1.11 逆矩阵的求法(一)
1.11.1 逆矩阵的性质

1.11.2 初等变换法求逆矩阵
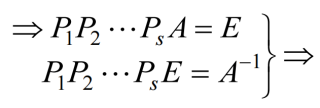

1.12 逆矩阵的求法(二)
1.12.1 定义法求逆矩阵

对n阶方阵A,只需找到一个n阶矩阵B,使AB=E或者BA=E就行了
例1

猜测
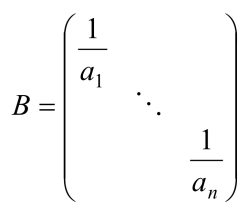
只须验证 AB=E
因此
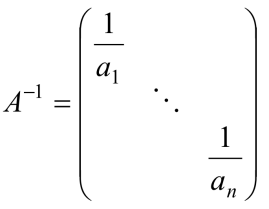
例2


例3
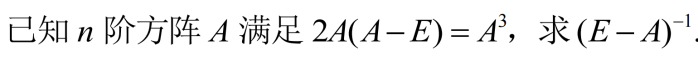

1.12.2 用定义证明B为A的逆
例1
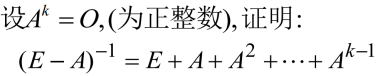
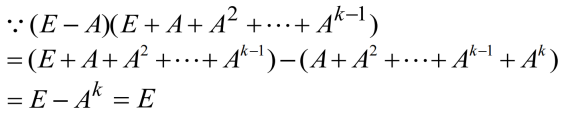
例2
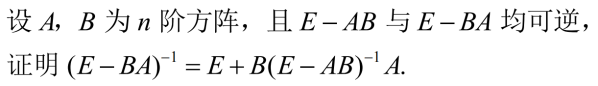

1.13 分块矩阵
1.13.1 分块矩阵的概念
将矩阵用若干纵横直线分成若干个小块,每一小块称为矩阵的子块(或子阵),以子块为元素形成的矩阵称为分块矩阵
例如
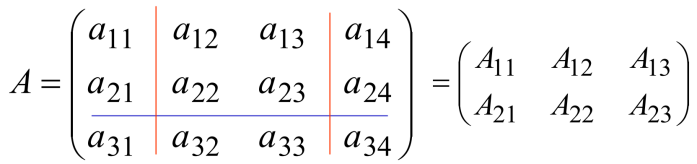
1.13.2 分块矩阵的运算
- 线性运算 加法与数乘
- 乘法运算 符合乘法的要求
- 转置运算 大块小块一起转
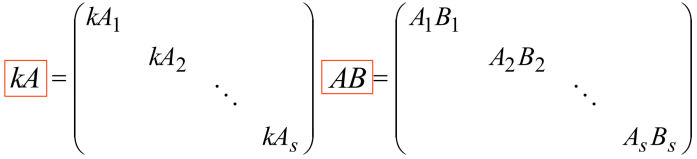
1.13.3 准对角阵

上面形式的分块矩阵即为准对角阵

如上图,则有


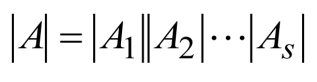
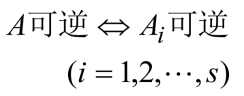
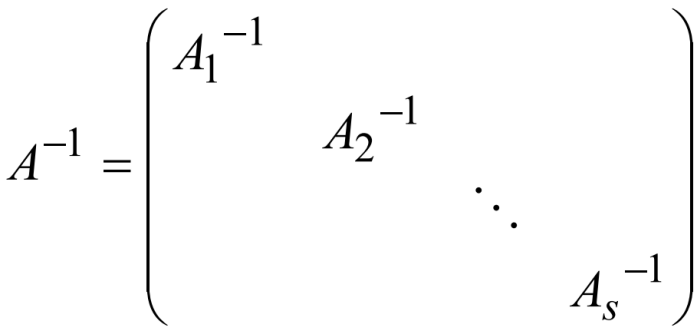
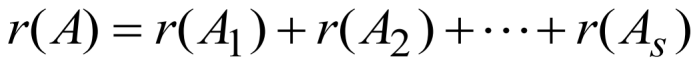
1.13.4 分块三角阵

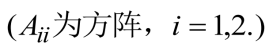
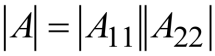


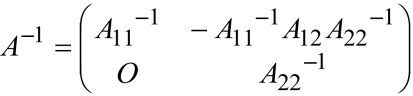
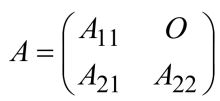

1.13.5 分块斜对角阵

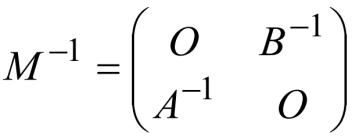
1.14 矩阵方程
1.14.1 AX=B
解法一
先求A的逆矩阵,再求
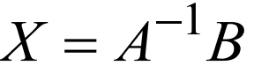
解法二
初等变换法
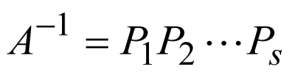

1.14.2 XA=B
解法一
先求A的逆,再求
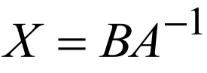
解法二
初等列变换法
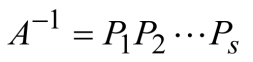
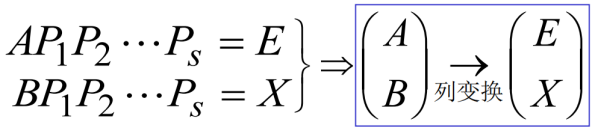
解法三
先两边取转置,再使用初等行变换
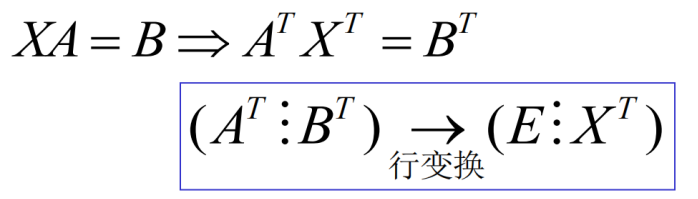
1.14.3 AXC=B
解法一
先分别求A和C的逆矩阵,再代入
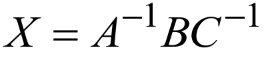
解法二
转化成前两种情形