【算法思想·二叉树】用「遍历」思维解题 II

本文参考labuladongsuanfa笔记[【强化练习】用「遍历」思维解题 II | labuladong 的算法笔记]

如果让你在二叉树中的某些节点上做文章，一般来说也可以直接用遍历的思维模式。

270. 最接近的二叉搜索树值 | 力扣 | LeetCode |

给你二叉搜索树的根节点 root 和一个目标值 target ，请在该二叉搜索树中找到最接近目标值 target 的数值。如果有多个答案，返回最小的那个。

示例 1：

输入：root = [4,2,5,1,3], target = 3.714286
输出：4

示例 2：

输入：root = [1], target = 4.428571
输出：1

提示：

树中节点的数目在范围 [1, 104] 内
0 <= Node.val <= 109
-109 <= target <= 109

基本思路

前文手把手刷二叉树总结篇说过二叉树的递归分为「遍历」和「分解问题」两种思维模式，这道题需要用到「遍历」的思维。

我们遍历 BST，施展 700. 二叉搜索树中的搜索的解法在 BST 中搜索 target，甭管能不能搜索到，一边搜索一边更新最接近 target 的值即可。

class Solution:
    def __init__(self):
        self.res = float('inf')

    def closestValue(self, root: TreeNode, target: float) -> int:
        self.traverse(root, target)
        return self.res

    # 遍历函数，在 BST 中搜索 target
    # 我们在中序位置写 if 判断逻辑，这样就可以从小到大执行，保证最终结果是值最小的
    def traverse(self, root: TreeNode, target: float) -> None:
        if root is None:
            return
        # 根据 target 和 root.val 的相对大小决定去左右子树搜索
        if root.val < target:
            # 中序位置（左子树遍历结束，准备遍历右子树时）
            if abs(root.val - target) < abs(self.res - target):
                self.res = root.val

            # 如果 target 比 root 大，那么 root 的左子树差值肯定更大，直接遍历右子树
            self.traverse(root.right, target)
        else:
            # 如果 target 比 root 小，那么 root 的右子树差值肯定更大，直接遍历左子树
            self.traverse(root.left, target)

            # 中序位置（左子树遍历结束，准备遍历右子树时）
            if abs(root.val - target) < abs(self.res - target):
                self.res = root.val

404. 左叶子之和 | 力扣 | LeetCode |

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

输入: root = [1]
输出: 0

提示:

节点数在 [1, 1000] 范围内
-1000 <= Node.val <= 1000

class Solution:

    def __init__(self):
        self.sum = 0

    # 记录左叶子之和
    # int sum = 0; # This is handled in the constructor now

    # 二叉树遍历函数
    def traverse(self, root):
        if root is None:
            return
        
        if root.left is not None and \
           root.left.left is None and root.left.right is None:
            # 找到左侧的叶子节点，记录累加值
            self.sum += root.left.val

        # 递归框架
        self.traverse(root.left)
        self.traverse(root.right)

    def sumOfLeftLeaves(self, root: TreeNode) -> int:
        self.traverse(root)
        return self.sum

623. 在二叉树中增加一行 | 力扣 | LeetCode |

给定一个二叉树的根 root 和两个整数 val 和 depth ，在给定的深度 depth 处添加一个值为 val 的节点行。

注意，根节点 root 位于深度 1 。

加法规则如下:

给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur ，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。
cur 原来的左子树应该是新的左子树根的左子树。
cur 原来的右子树应该是新的右子树根的右子树。
如果 depth == 1 意味着 depth - 1 根本没有深度，那么创建一个树节点，值 val 作为整个原始树的新根，而原始树就是新根的左子树。

示例 1:

输入: root = [4,2,6,3,1,5], val = 1, depth = 2
输出: [4,1,1,2,null,null,6,3,1,5]

示例 2:

输入: root = [4,2,null,3,1], val = 1, depth = 3
输出:  [4,2,null,1,1,3,null,null,1]

提示:

节点数在 [1, 104] 范围内
树的深度在 [1, 104]范围内
-100 <= Node.val <= 100
-105 <= val <= 105
1 <= depth <= the depth of tree + 1

class Solution:
    def __init__(self):
        self.targetVal = 0
        self.targetDepth = 0

    def addOneRow(self, root: TreeNode, val: int, depth: int) -> TreeNode:
        self.targetVal = val
        self.targetDepth = depth
        # 插入到第一行的话特殊对待一下
        if self.targetDepth == 1:
            newRoot = TreeNode(self.targetVal)
            newRoot.left = root
            return newRoot
        # 遍历二叉树，走到对应行进行插入
        self.traverse(root, 1)

        return root

    def traverse(self, root: TreeNode, curDepth: int):
        if root is None:
            return
        # 前序遍历
        if curDepth == self.targetDepth - 1:
            # 进行插入
            newLeft = TreeNode(self.targetVal)
            newRight = TreeNode(self.targetVal)
            newLeft.left = root.left
            newRight.right = root.right
            root.left = newLeft
            root.right = newRight
        # Recursively traverse the left and right subtree
        self.traverse(root.left, curDepth + 1)
        self.traverse(root.right, curDepth + 1)

971. 翻转二叉树以匹配先序遍历 | 力扣 | LeetCode |

给你一棵二叉树的根节点 root ，树中有 n 个节点，每个节点都有一个不同于其他节点且处于 1 到 n 之间的值。

另给你一个由 n 个值组成的行程序列 voyage ，表示预期的二叉树先序遍历结果。

通过交换节点的左右子树，可以翻转该二叉树中的任意节点。例，翻转节点 1 的效果如下：

请翻转最少的树中节点，使二叉树的 先序遍历 与预期的遍历行程 voyage 相匹配 。

如果可以，则返回 翻转的 所有节点的值的列表。你可以按任何顺序返回答案。如果不能，则返回列表 [-1]。

示例 1：

输入：root = [1,2], voyage = [2,1]
输出：[-1]
解释：翻转节点无法令先序遍历匹配预期行程。

示例 2：

输入：root = [1,2,3], voyage = [1,3,2]
输出：[1]
解释：交换节点 2 和 3 来翻转节点 1 ，先序遍历可以匹配预期行程。

示例 3：

输入：root = [1,2,3], voyage = [1,2,3]
输出：[]
解释：先序遍历已经匹配预期行程，所以不需要翻转节点。

提示：

树中的节点数目为 n
n == voyage.length
1 <= n <= 100
1 <= Node.val, voyage[i] <= n
树中的所有值 互不相同
voyage 中的所有值 互不相同

用 traverse 函数遍历整棵二叉树，对比前序遍历结果，如果节点的值对不上，就无解；如果子树对不上 voyage，就尝试翻转子树。

class Solution:
    def flipMatchVoyage(self, root: TreeNode, voyage: List[int]) -> List[int]:
        self.res = []
        self.i = 0
        self.can_flip = True
        
        def dfs(node):
            # 遍历的过程中尝试进行反转
            if not node or not self.can_flip:
                return True
            if node.val != voyage[self.i]:
                # 节点的 val 对不上，必然无解
                self.can_flip = False
                return False
            self.i += 1
            # Only flip if there's a left child and the next value in voyage doesn't match the left child's value
            if node.left and node.left.val != voyage[self.i]:
                # 前序遍历结果不对，尝试翻转左右子树
                self.res.append(node.val)
                node.left, node.right = node.right, node.left
            # 记录翻转节点
            # Note: This comment was not in the original Java code, but added to match the pattern of comments. 
            # If this was not intended, it can be removed.
            return dfs(node.left) and dfs(node.right)
        
        if dfs(root):
            return self.res
        else:
            return [-1]

987. 二叉树的垂序遍历 | 力扣 | LeetCode |

给你二叉树的根结点 root ，请你设计算法计算二叉树的 垂序遍历 序列。

对位于 (row, col) 的每个结点而言，其左右子结点分别位于 (row + 1, col - 1) 和 (row + 1, col + 1) 。树的根结点位于 (0, 0) 。

二叉树的 垂序遍历 从最左边的列开始直到最右边的列结束，按列索引每一列上的所有结点，形成一个按出现位置从上到下排序的有序列表。如果同行同列上有多个结点，则按结点的值从小到大进行排序。

返回二叉树的 垂序遍历 序列。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[9],[3,15],[20],[7]]
解释：
列 -1 ：只有结点 9 在此列中。
列  0 ：只有结点 3 和 15 在此列中，按从上到下顺序。
列  1 ：只有结点 20 在此列中。
列  2 ：只有结点 7 在此列中。

示例 2：

输入：root = [1,2,3,4,5,6,7]
输出：[[4],[2],[1,5,6],[3],[7]]
解释：
列 -2 ：只有结点 4 在此列中。
列 -1 ：只有结点 2 在此列中。
列  0 ：结点 1 、5 和 6 都在此列中。
          1 在上面，所以它出现在前面。
          5 和 6 位置都是 (2, 0) ，所以按值从小到大排序，5 在 6 的前面。
列  1 ：只有结点 3 在此列中。
列  2 ：只有结点 7 在此列中。

示例 3：

输入：root = [1,2,3,4,6,5,7]
输出：[[4],[2],[1,5,6],[3],[7]]
解释：
这个示例实际上与示例 2 完全相同，只是结点 5 和 6 在树中的位置发生了交换。
因为 5 和 6 的位置仍然相同，所以答案保持不变，仍然按值从小到大排序。

提示：

树中结点数目总数在范围 [1, 1000] 内
0 <= Node.val <= 1000

看这题的难度是困难，但你别被吓住了，我们从简单的开始，如果以整棵树的根节点为坐标 (0, 0)，你如何打印出其他节点的坐标？

很简单，写出如下代码遍历一遍二叉树即可：

void traverse(TreeNode root, int row, int col) {
    if (root == null) {
        return;
    }
    print(row, col);
    traverse(root.left, row + 1, col - 1);
    traverse(root.right, row + 1, col + 1);
}

然后就简单了，把这些坐标收集起来，依据题目要求进行排序，组装成题目要求的返回数据格式即可。

class Solution:
    # 记录每个节点和对应的坐标 (row, col)
    class Triple:
        def __init__(self, node, row, col):
            self.node = node
            self.row = row
            self.col = col

    def verticalTraversal(self, root: TreeNode) -> List[List[int]]:
        # 遍历二叉树，并且为所有节点生成对应的坐标
        self.traverse(root, 0, 0)
        # 根据题意，根据坐标值对所有节点进行排序：
        # 按照 col 从小到大排序，col 相同的话按 row 从小到大排序，
        # 如果 col 和 row 都相同，按照 node.val 从小到大排序。
        self.nodes.sort(key=lambda x: (x.col, x.row, x.node.val))
        # 将排好序的节点组装成题目要求的返回格式
        res = collections.deque()
        # 记录上一列编号，初始化一个特殊值
        preCol = float('-inf')
        for cur in self.nodes:
            if cur.col != preCol:
                # 开始记录新的一列
                res.append(collections.deque())
                preCol = cur.col
            res[-1].append(cur.node.val)

        return [list(col) for col in res]

    def __init__(self):
        self.nodes = []
        
    # 二叉树遍历函数，记录所有节点对应的坐标
    def traverse(self, root: TreeNode, row: int, col: int):
        if root is None:
            return
        # 记录坐标
        self.nodes.append(self.Triple(root, row, col))
        # 二叉树遍历框架
        self.traverse(root.left, row + 1, col - 1)
        self.traverse(root.right, row + 1, col + 1)

tips

1、关于 Triple 对象，写成内部类和外部类在新建对象的时候表示方法不同，注意区别。

2、res = collections.deque() 就是新建一个双端队列，注意尾部的括号（）别掉。

3、整体思路就是先遍历整颗树，把每个节点的行坐标和列坐标记录下来，然后对其排序（优先级：列>行>值）。

4、最后把排好序的self.nodes根据列坐标依次添加到res队列中，最后再将队列转化为List返回即可。

993. 二叉树的堂兄弟节点 | 力扣 | LeetCode |

在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k+1 处。

如果二叉树的两个节点深度相同，但 父节点不同 ，则它们是一对堂兄弟节点。

我们给出了具有唯一值的二叉树的根节点 root ，以及树中两个不同节点的值 x 和 y 。

只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true 。否则，返回 false。

示例 1：

输入：root = [1,2,3,4], x = 4, y = 3
输出：false

示例 2：

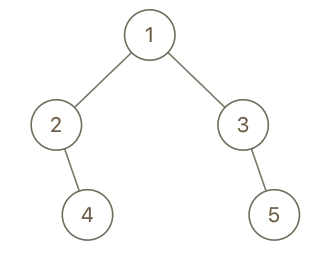
输入：root = [1,2,3,null,4,null,5], x = 5, y = 4
输出：true

示例 3：

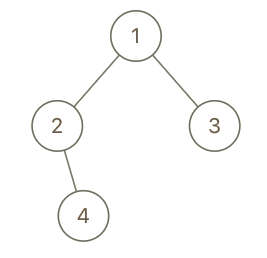
输入：root = [1,2,3,null,4], x = 2, y = 3
输出：false

提示：

二叉树的节点数介于 2 到 100 之间。
每个节点的值都是唯一的、范围为 1 到 100 的整数。

遍历找到 x，y 的深度和父节点，对比即可。

class Solution:
    def __init__(self):
        self.parentX = None
        self.parentY = None
        self.depthX = 0
        self.depthY = 0
        self.x = 0
        self.y = 0

    def isCousins(self, root: TreeNode, x: int, y: int) -> bool:
        self.x = x
        self.y = y
        self.traverse(root, 0, None)
        if self.depthX == self.depthY and self.parentX != self.parentY:
            # 判断 x，y 是否是表兄弟节点
            return True
        return False

    def traverse(self, root: TreeNode, depth: int, parent: TreeNode) -> None:
        if root is None:
            return
        if root.val == self.x:
            # 找到 x，记录它的深度和父节点
            self.parentX = parent
            self.depthX = depth
        if root.val == self.y:
            # 找到 y，记录它的深度和父节点
            self.parentY = parent
            self.depthY = depth
        self.traverse(root.left, depth + 1, root)
        self.traverse(root.right, depth + 1, root)

1315. 祖父节点值为偶数的节点和 | 力扣 | LeetCode |

给你一棵二叉树，请你返回满足以下条件的所有节点的值之和：

该节点的祖父节点的值为偶数。（一个节点的祖父节点是指该节点的父节点的父节点。）

如果不存在祖父节点值为偶数的节点，那么返回 0 。

示例：

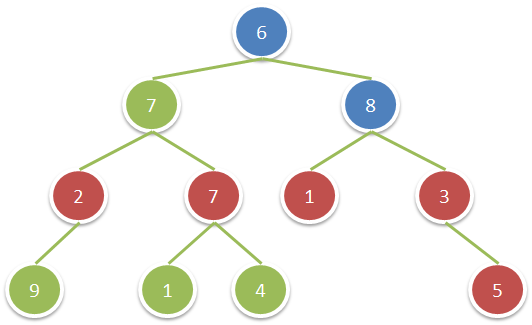
输入：root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
输出：18
解释：图中红色节点的祖父节点的值为偶数，蓝色节点为这些红色节点的祖父节点。

提示：

树中节点的数目在 1 到 10^4 之间。
每个节点的值在 1 到 100 之间。

class Solution:
    def __init__(self):
        self.sum = 0

    def sumEvenGrandparent(self, root: TreeNode) -> int:
        self.traverse(root)
        return self.sum

    # 二叉树的遍历函数
    def traverse(self, root: TreeNode):
        if root is None:
            return
        if root.val % 2 == 0:
            # 累加左子树孙子节点的值
            if root.left is not None:
                if root.left.left is not None:
                    self.sum += root.left.left.val
                if root.left.right is not None:
                    self.sum += root.left.right.val

            # 累加右子树孙子节点的值
            if root.right is not None:
                if root.right.left is not None:
                    self.sum += root.right.left.val
                if root.right.right is not None:
                    self.sum += root.right.right.val

        # 二叉树的遍历框架
        self.traverse(root.left)
        self.traverse(root.right)

1448. 统计二叉树中好节点的数目 | 力扣 | LeetCode |

给你一棵根为 root 的二叉树，请你返回二叉树中好节点的数目。

「好节点」X 定义为：从根到该节点 X 所经过的节点中，没有任何节点的值大于 X 的值。

示例 1：

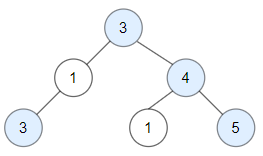
输入：root = [3,1,4,3,null,1,5]
输出：4
解释：图中蓝色节点为好节点。
根节点 (3) 永远是个好节点。
节点 4 -> (3,4) 是路径中的最大值。
节点 5 -> (3,4,5) 是路径中的最大值。
节点 3 -> (3,1,3) 是路径中的最大值。

示例 2：

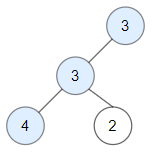
输入：root = [3,3,null,4,2]
输出：3
解释：节点 2 -> (3, 3, 2) 不是好节点，因为 "3" 比它大。

示例 3：

输入：root = [1]
输出：1
解释：根节点是好节点。

提示：

二叉树中节点数目范围是 [1, 10^5] 。
每个节点权值的范围是 [-10^4, 10^4] 。

class Solution:
    def __init__(self):
        self.count = 0

    def goodNodes(self, root: TreeNode) -> int:
        self.traverse(root, root.val)
        return self.count

    # 二叉树遍历函数，pathMax 参数记录从根节点到当前节点路径中的最大值
    def traverse(self, root: TreeNode, pathMax: int):
        if root is None:
            return
        if pathMax <= root.val:
            # 找到一个「好节点」
            self.count += 1
        # 更新路径上的最大值
        pathMax = max(pathMax, root.val)

        self.traverse(root.left, pathMax)
        self.traverse(root.right, pathMax)

1469. 寻找所有的独生节点 | 力扣 | LeetCode |

二叉树中，如果一个节点是其父节点的唯一子节点，则称这样的节点为 “独生节点” 。二叉树的根节点不会是独生节点，因为它没有父节点。

给定一棵二叉树的根节点 root ，返回树中 所有的独生节点的值所构成的数组 。数组的顺序不限。

示例 1：

输入：root = [1,2,3,null,4]
输出：[4]
解释：浅蓝色的节点是唯一的独生节点。
节点 1 是根节点，不是独生的。
节点 2 和 3 有共同的父节点，所以它们都不是独生的。

示例 2：

输入：root = [7,1,4,6,null,5,3,null,null,null,null,null,2]
输出：[6,2]
输出：浅蓝色的节点是独生节点。
请谨记，顺序是不限的。 [2,6] 也是一种可接受的答案。

示例 3：

输入：root = [11,99,88,77,null,null,66,55,null,null,44,33,null,null,22]
输出：[77,55,33,66,44,22]
解释：节点 99 和 88 有共同的父节点，节点 11 是根节点。
其他所有节点都是独生节点。

提示：

tree 中节点个数的取值范围是 [1, 1000]。
1 <= Node.val <= 106

class Solution:
    def getLonelyNodes(self, root: TreeNode) -> List[int]:
        self.res = []
        self.traverse(root, False)
        return self.res

    # 二叉树遍历函数
    def traverse(self, root: TreeNode, is_root: bool) -> None:
        if root is None:
            return
        
        # 发现独生节点
        # Only add the child node if it is a lonely node (has no sibling and is not the root node)
        if not is_root:
            if (root.left is None and root.right is not None) or (root.left is not None and root.right is None):
                self.res.append(root.left.val) if root.left else self.res.append(root.right.val)

        # 二叉树遍历框架
        # Recursively traverse the left and right children, the second parameter is False now because we are going deeper
        self.traverse(root.left, False)
        self.traverse(root.right, False)

1602. 找到二叉树中最近的右侧节点 | 力扣 | LeetCode |

给定一棵二叉树的根节点 root 和树中的一个节点 u ，返回与 u 所在层中距离最近的右侧节点，当 u 是所在层中最右侧的节点，返回 null 。

示例 1：

输入：root = [1,2,3,null,4,5,6], u = 4
输出：5
解释：节点 4 所在层中，最近的右侧节点是节点 5。

示例 2：

输入：root = [3,null,4,2], u = 2
输出：null
解释：2 的右侧没有节点。

示例 3：

输入：root = [1], u = 1
输出：null

示例 4：

输入：root = [3,4,2,null,null,null,1], u = 4
输出：2

提示:

树中节点个数的范围是 [1, 105] 。
1 <= Node.val <= 105
树中所有节点的值是唯一的。
u 是以 root 为根的二叉树的一个节点。

这道题的直接思路是用 BFS 层序遍历算法，肯定可以找到节点 u 的相邻节点。

如果你熟悉二叉树的前中后序遍历的顺序，就知道前序遍历也可以找到 u 的相邻节点：

先找到 u 的层数 targetDepth，然后再次走到 targetDepth 时遇到的就是 u 的相邻节点。

class Solution:
    def findNearestRightNode(self, root: TreeNode, u: TreeNode) -> TreeNode:
        self.targetDepth = -1
        self.res = None
        self.traverse(root, 0, u.val)
        return self.res
    
    # 二叉树遍历函数
    def traverse(self, root: TreeNode, depth: int, targetVal: int) -> None:
        if not root or self.res:
            return
        
        if targetVal == root.val:
            # 找到目标层数
            self.targetDepth = depth
        elif depth == self.targetDepth:
            # 找到下一个当前层数的节点
            self.res = root
            return
        
        # 二叉树遍历框架
        self.traverse(root.left, depth + 1, targetVal)
        self.traverse(root.right, depth + 1, targetVal)