week 60 NLA-GNN

摘要

本周阅读了题为NLA-GNN: Non-local information aggregated graph neural network for heterogeneous graph embedding的论文。该文提出了一种新的框架——非局部信息聚合图神经网络(NLA-GNN)，旨在更有效地探索异构图。该框架结合了本地和非本地的节点属性聚合机制，其中本地层聚焦于邻近节点，而非本地层则通过注意力机制选取重要远程节点的信息。实验表明NLA-GNN表现出色，并且非本地层对于性能提升至关重要。此方法利用全局注意机制和一维卷积来捕捉远距离节点间的依赖关系，但大规模应用时内存消耗较大，未来工作将考虑分布式聚合以适应更大规模的数据集。

Abstract

This week’s weekly newspaper decodes the paper entitled NLA-GNN: Non-local information aggregated graph neural network for heterogeneous graph embedding. The paper introduces a novel framework, the Non-Local Information Aggregation Graph Neural Network (NLA-GNN), aimed at exploring heterogeneous graphs more effectively. This framework integrates both local and non-local node attribute aggregation mechanisms, with the local layer focusing on nearby nodes, and the non-local layer selecting information from significant distant nodes through an attention mechanism. Experiments show that the NLA-GNN performs excellently, and the non-local layer is crucial for performance enhancement. The method leverages global attention mechanisms and 1D convolutions to capture dependencies between distant nodes. However, when applied on a large scale, it requires substantial memory for global attention extraction, posing a challenge for deployment on smaller machines. Future work will consider distributed aggregation to accommodate larger datasets.

一、文献阅读

1. 题目

标题：NLA-GNN: Non-local information aggregated graph neural network for heterogeneous graph embedding

作者：Siheng Wang, Guitao Cao, Wenming Cao, Yan Li

发布：pattern recognition二区

链接：https://doi.org/10.1016/j.patcog.2024.110940

2. Abstract

本文提出了一种新的非局部信息聚合图神经网络(NLA-GNN)，它不仅可以聚合来自邻近节点的局部信息，还可以聚合来自远距离节点的非局部信息。具体来说，NLA-GNN中的局部聚合模块利用注意机制生成潜在有价值的元路径，并使用它们来聚合局部信息。非局部聚合模块采用两步方法，每一步都采用注意力引导的方法将节点排序到节点序列中，并使用为序列数据设计的方法进行信息聚合。在三个异构图数据集上的实验结果表明，NLA-GNN的性能超越了最先进的技术，并且证明了在异构图中进行非局部聚合的必要性。

3. 文献解读

3.1 Introduction

为了实现异构图中的非局部信息聚合，提出了一种新的非局部信息聚合图神经网络(NLA-GNN)，该网络可以有效地聚合来自局部和非局部节点的信息。在保持模型层数较低的同时，实现了对远程节点依赖关系的有效捕获，从而有效地缓解了过度平滑问题。

NLA-GNN由本地聚合模块和非本地聚合模块组成。给定节点的属性和异构图的结构，使用局部聚合模块层来学习不同边缘类型的潜在有价值的组合。通过堆叠多个这样的层，本地聚合模块可以捕获有价值的元路径，从而启用本地聚合。此外，利用两步方法来启用非本地聚合。在每一步中，将节点排序到节点序列中。由于节点的排序是由注意机制引导的，节点序列中相邻的两个节点在原图结构中可能相距很远。然后对这些节点序列进行一维卷积，对序列中相邻节点的属性进行聚合。这也意味着原始图中彼此相距很远的节点的属性现在可以聚合了。

因此，模型可以从本地和非本地邻居端到端聚合有用的表示。在三个异构图数据集上的实验结果表明，NLA-GNN达到了最先进的性能。

3.2 创新点

该文的主要贡献有三个方面：

1. 提出了一种新的框架，称为NLA-GNN，用于生成有意义的低维节点嵌入。方法同时考虑局部和非局部信息，而不是像其他方法那样只考虑异构图中的局部信息。因此，NLA-GNN可以有效地探索异构图，从局部和非局部节点中聚合信息。
2. 提出了一种两步方法来实现异构图的非局部聚合:类型步和全局步。按类型步骤关注每个节点类型，而全局步骤关注异构图中的所有节点。这些步骤中的每一步都使用注意力引导方法将节点排序到节点序列中，并使用为顺序数据设计的方法聚合信息。
3. 比较了NLA-GNN与不同基线方法，包括传统的图嵌入方法和图神经网络方法。在三个数据集上的实验表明，方法优于最先进的方法。

4. 网络结构

$$

$$

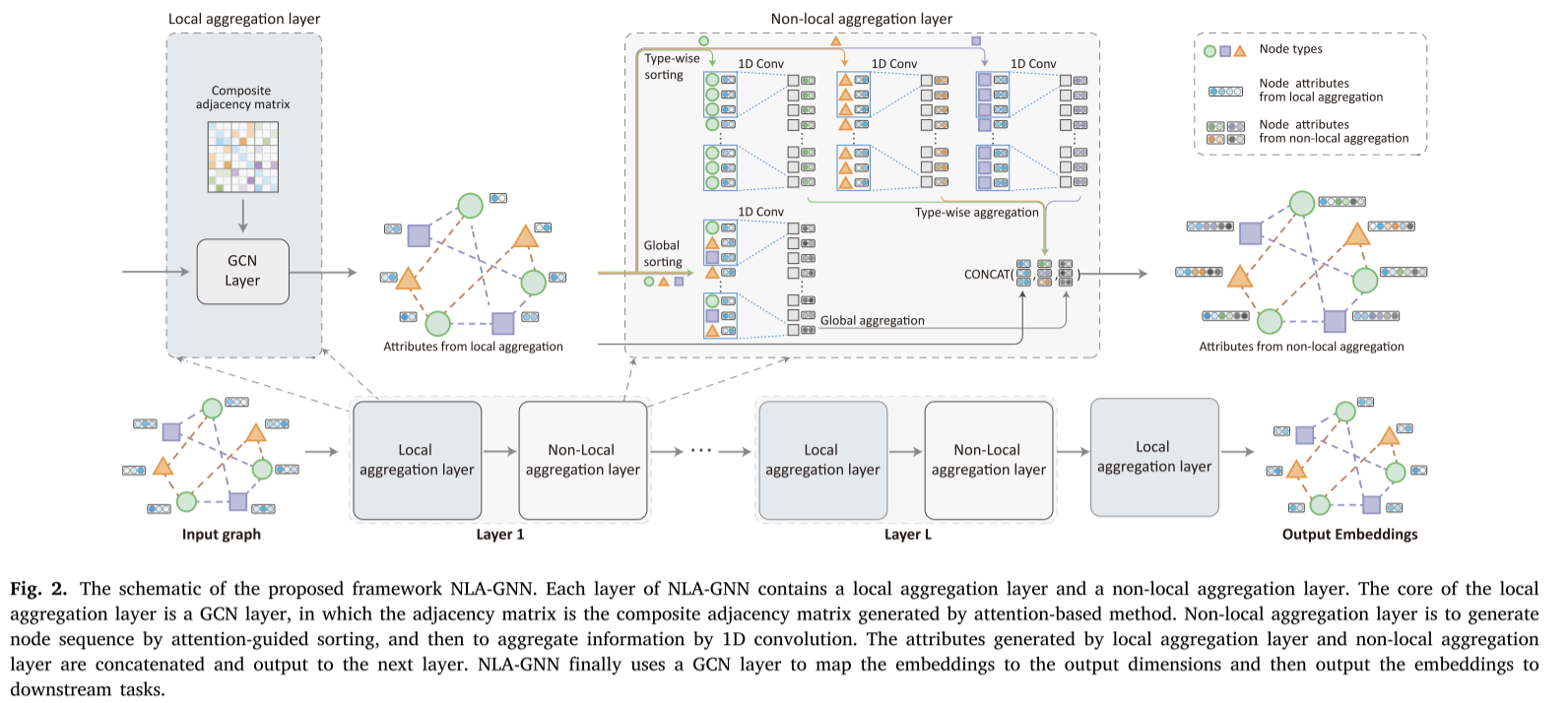
该文提出了一个新的框架NLA-GNN，它可以聚合来自本地邻居和远程节点的信息来生成异构图的嵌入。图2给出了NLA-GNN的整体框架。NLA-GNN由多层组成，每层包含两个聚合层:本地聚合层和非本地聚合层(NL-Layer)。具体来说，NLA-GNN利用基于注意力的方法来组成每个边类型的邻接矩阵，因此可以将异构图视为同质图，并使用图卷积网络(GCN)层与复合邻接矩阵实现局部聚合。在本地聚合层之后，非本地聚合层根据节点的类型将节点划分为𝐾𝑣类。它使用注意力引导排序来打乱每个类中节点的顺序(类型排序)。此外，非局部聚合层对图中的所有节点进行洗牌，而不管它们的类型(全局排序)。然后，排序后的节点形成多节点序列。nl层对每个序列使用一维卷积神经网络层进行信息聚合。由于排序过程是注意力引导的，并且与图结构无关，因此节点可以从非局部节点中聚合信息。在框架的最后，使用一个额外的本地聚合层将嵌入映射到指定的维度，然后可以用于下游任务。

4.1 复合邻接矩阵

异构图中存在多个邻接矩阵。每种类型的边$t_i\in {\mathcal{T}}^e$对应一个邻接矩阵$A_{t_i}$​。探索不同局部关系结构的直观思路是计算具有归一化系数的多个邻接矩阵的线性组合。也就是说,
$$A^{(l)}=\sum _{t_i\in {\mathcal{T}}^e}{\alpha }_{t_i}^{(l)}{A}_{t_i}$$
学习了𝐿层的复合邻接矩阵后，将每层的复合邻接矩阵相乘即可得到长度为𝐿元路径的邻接矩阵。也就是说,
$$A_p=A^{(1)}{A}^{(2)}\dots A^{(L)}$$
$A_P$为基于元路径的图${\mathcal{G}}^P$邻接矩阵。注意，矩阵$A_P$包含多个潜在的元路径。由于复合邻接矩阵$A^{(l)}$的每一层都是由多个不同边型的邻接矩阵$A_{t_i}$构成的，所以每一层的几个边型即构成元路径。通过多层相乘，多个不同权值的元路径形成矩阵$A_P$

然而，使用Eq.(2)生成复合邻接矩阵有一个缺点。因为$A_P$中每个元路径的长度都是L，所以$A_P$无法捕获短元路径。为了解决这个问题，在邻接矩阵合成过程中引入单位矩阵$A_t\in R^{N\times N}$。因此，该模型既可以从原始邻接矩阵合成矩阵，也可以从自连接矩阵合成矩阵。自连接不会增加元路径的长度。因此，可以将Eq.(2)修改为:
A ( l ) = ∑ t i ∈ T e α t i ( l ) A t i + α I ( l ) A I = ∑ t i ∈ { T e , I } α t i ( l ) A t i A^{(l)}=\sum_{t_i\in\mathcal T^e}\alpha^{(l)}_{t_i}A_{t_i}+\alpha^{(l)}_IA_I=\sum_{t_i\in\{\mathcal T^e,I\}}\alpha^{(l)}_{t_i}A_{t_i} A(l)=ti​∈Te∑​αti​(l)​Ati​​+αI(l)​AI​=ti​∈{Te,I}∑​αti​(l)​Ati​​
可以将Eq.(4)中的系数用softmax修改为:
$$\begin{gathered} a^{(l)}=\{\begin{array}{l}\text{exp}(s_{t_i}^{(l)}{t}_{t_i}^{(l)})/z^{(l)}{t}_i\in {\mathcal{T}}^e\\ \text{exp}(a_l)/z^{(l)}{t}_i=I\end{array} \\ {z}^{(l)}=\sum _{t_i\in {\mathcal{T}}^e}\text{exp}(s_{t_i}^{(l)}{t}_{t_i}^{(l)})+\text{exp}({\alpha }_l) \end{gathered}$$
令
$$s_{t_i}^{(l)}=\{\begin{array}{l}{s}_{t_i}^{(l)}l=1t_{t_i}^{(l-1)}2\le l\le L\end{array}$$

4.2 局部聚合

为了实现局部聚合，考虑使用GCN层和学习到的复合邻接矩阵对局部邻居进行信息聚合。也就是说,
$$H_{local}^{(l)}=f^{(l)}(H^{(l-1)},A^{(l)})=\sigma (A^{(l)}{H}^{(l-1)}{W}^{(l)})$$
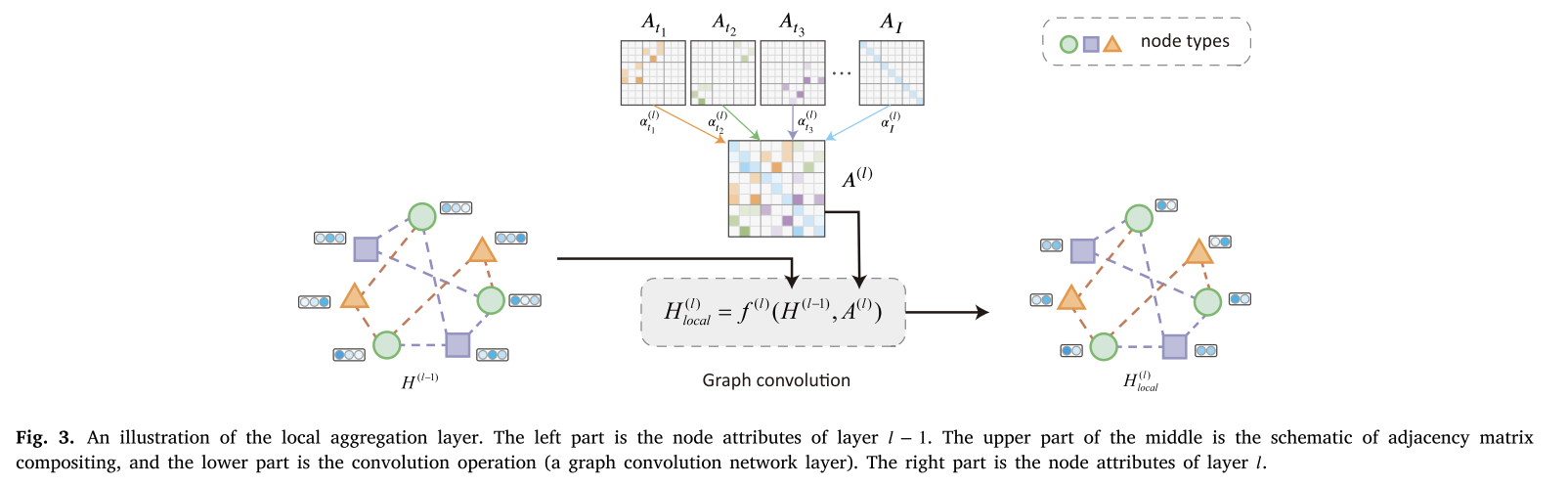
图3是局部聚合层的图示。首先，使用注意机制从不同类型的边学习一个复合邻接矩阵。然后，通过卷积运算𝑓(𝑙)(⋅)对𝑙−1层的属性进行聚合。应用卷积运算𝑓(𝑙)(⋅)后，卷积图通过不同类型的边以自动学习到的不同权值对信息进行聚合。

4.3 非局部聚合

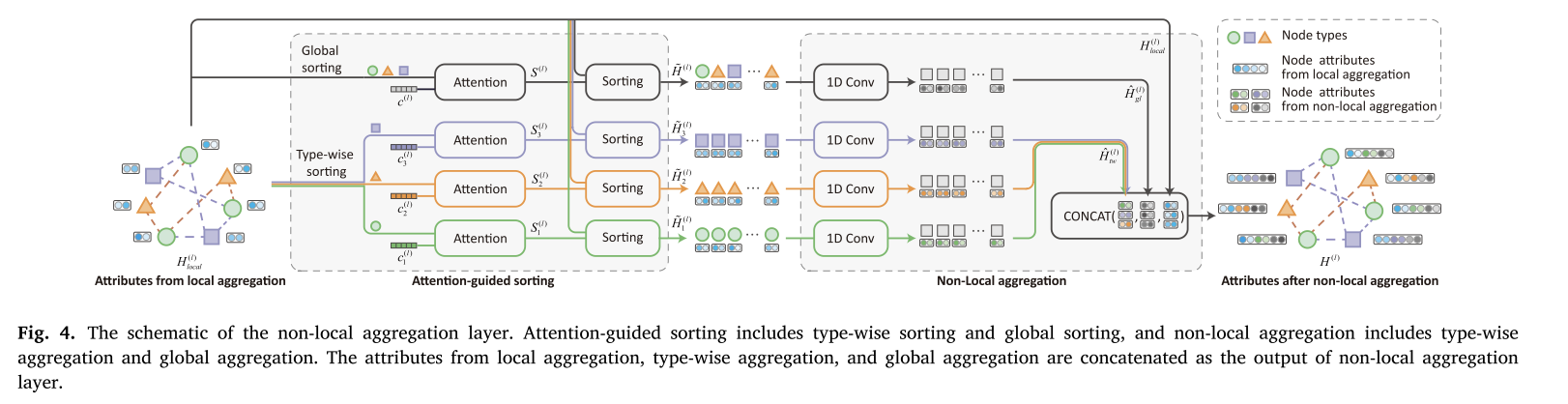
图中没有固定的节点顺序。实现非局部聚合的关键思想是利用注意机制对节点进行排序，排序后的节点可以看作是一个节点序列。如图4所示，为了处理节点序列，可以使用针对序列数据设计的传统方法。由于节点的排序是由注意机制引导的，节点序列中相邻的两个节点在原图结构中可能相距很远。经过一维卷积后，对序列中相邻节点的属性进行聚合。这也意味着原始图中彼此相距很远的节点的属性现在可以聚合了。

异构图的思想是以两种不同的方式对节点进行排序:类型排序和全局排序。在类型排序中，根据节点的类型对其进行分类，并对每个类分别使用注意引导排序。在全局排序中，对所有节点使用注意力引导排序。在注意引导排序之后，使用1D卷积神经网络对每个序列的属性进行聚合。

4.4 多频

需要注意的是，NLA-GNN框架中的可训练参数是随机初始化的，这可能导致算法陷入局部最优。利用算法中的多通道来提高NLA-GNN的性能。不同通道的节点属性表示为 { H ( 1 ) , H ( 2 ) , … H ( C ) } \{H^{(1)},H^{(2)},\dots H^{(C)}\} {H(1),H(2),…H(C)}​，其中扮成为通道数。从NLA-GNN中学习到的最终属性由所有分布的平均值计算:
$${\tilde{H}}_{out}=\frac{1}{C}\sum _{c=1}^C{H}_{out}^{[c]}$$

4.5 NLA-GNN算法

如算法1所示，给定初始节点特征𝑿和每种类型$t_1$邻接矩阵$A_{t_i}$，首先为每层𝑙计算一个复合邻接矩阵(𝑙)，然后使用本地聚合模块(即Eq.(7))从最后一层$H^{(l)}$计算$H_{local}^{(l)}$。然后使用非局部聚合模块计算${\hat{H}}^{(l)}$作为下一层的输入。叠加𝐿层后，从层𝐿的非线性聚合模块中得到${\hat{H}}^{(L)}$)。为了降低${\hat{H}}^{(L)}$的维数，使用了一个额外的局部聚合层，并获得了可用于下游任务的最终嵌入$H_{out}$​。

5. 实验过程

5.1 参数设置

数据集：使用[2]中提供的三个异构图，大致情况如表二

• DBLP。它是一个引文网络数据集，包含三种类型的节点(论文§、作者(a)和会议©)和四种类型的边(P- a、a -P、P-C、C-P)。DBLP的标签是作者的研究领域，包括数据挖掘、数据库、信息检索和机器学习。
• ACM。ACM有三种类型的节点(Papers §、Authors (A)和Subjects (S))和四种类型的边(P-A、A-P、P-S、S-P)。它是一个引文网络数据集，以论文类别(数据挖掘、无线通信、数据库)为标签。
• IMDB。它是关于电影和相关信息的网站的一个子集。它包含三种类型的节点:Movie (M)、Director (D)和Actor (A)，以及四个作为边的关系:M-D、D-M、M-A、A-M。IMDB的标签是电影的类型，包括喜剧、动作和戏剧。

将NLA-GNN与传统的网络嵌入方法、针对同质图设计的基于图神经网络的方法和基于异构图神经网络的方法进行了比较，以评估方法的有效性。

基线：

1. 传统的网络嵌入方法:
   • DeepWalk:一种基于随机行走的方法，它可以从齐次图中生成嵌入。本文将所有的节点和边都看作一种类型，以便在异构图上执行齐次方法。
   • Metapath2Vec:一种基于元路径的异构图随机漫步方法。Metapath2Vec使用跳过图方法生成嵌入。
2. 基于图神经网络的方法:
   • GCN:齐次图神经网络采用谱图卷积的局部一阶逼近来聚合邻近节点的表示。这里将所有的节点和边都视为一种类型，以便在异构图上执行GCN。
   • GAT:一种利用注意机制为不同邻居指定不同权值的同构图神经网络。这里忽略节点和边的类型，以便在异构图上实现GAT。
3. 基于异构图神经网络的方法:
   • HAN:一种利用注意机制生成嵌入的异构图神经网络。HAN需要手动选择元路径。
   • MAGNN:一种考虑元路径中间节点并需要预定义元路径的异构图神经网络。
   • GTN:一种自动学习元路径的异构图神经网络。这里不需要预定义的元路径。

实现细节：将隐藏维度设置为64，并对所有模型使用相同的数据集。随机初始化参数，并以Adam为优化器。对于GCN、GAT、HAN、MAGNN和GTN，利用验证集来优化参数，并对IMDB使用预定义元路径MAM和MDM，对ACM使用预定义元路径PAP和PSP，对DBLP使用预定义元路径APA和APCPA。对于GAT和HAN，选择头数为8。在提出的NLA-GNN中，信道数设置为2，其中IMDB和DBLP为3层(包括附加的本地聚合层)，ACM为2层。权重衰减设为0.001，学习率设为0.005。

5.2 实验结果

将该方法与几种异构图神经网络模型，以及几种具有代表性的传统网络嵌入模型和同质图模型进行了比较。同构图模型在应用于异构图数据时表现出较低的性能。因此，只选取两个典型的同构图模型来展示实验结果。节点分类定量实验结果如表3所示。在表中，将微观f1表示为Mi-F1，宏观f1表示为Ma-F1。对每个数据集进行了20次实验运行，随后计算结果的平均值和标准差。统计显著性分析采用Welch’s t检验。

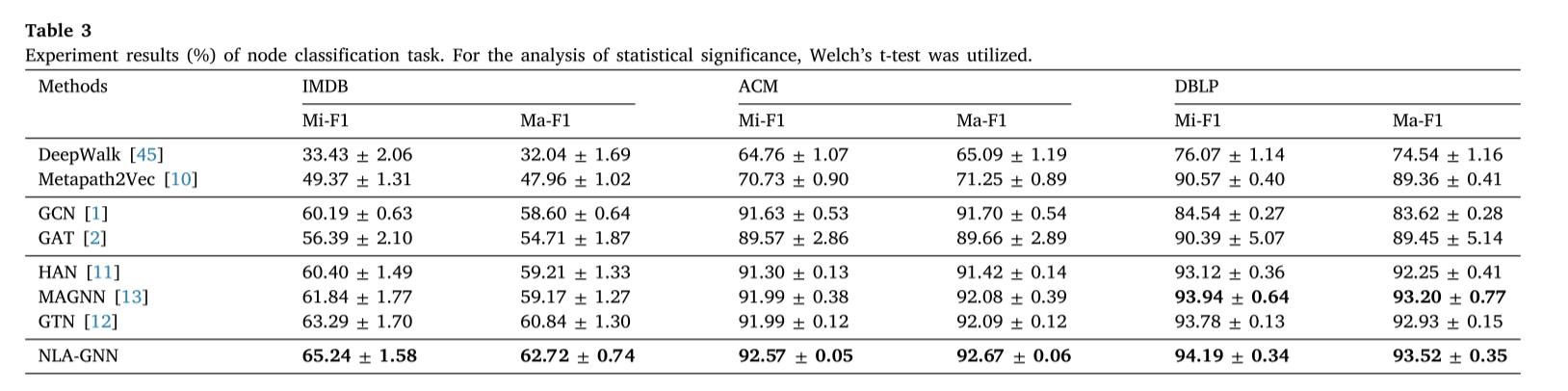
• 传统的网络嵌入方法在大多数数据集上的性能不如神经网络方法，这可能是由于在使用模型处理复杂的异构图数据时，只考虑了图的结构信息，而忽略了节点属性信息。
• 同构图神经网络(GCN, GAT)比传统的嵌入方法更好，可能是因为图神经网络可以更有效地探索图的结构。然而，它们是为同构图设计的，因此在异构图上的表现不如在同构图上的表现。
• 异构图神经网络可以捕获复杂的异构结构，获得有意义的嵌入，在节点分类任务中表现优于其他方法。此外，方法NLA-GNN优于以往的最先进的技术，性能的提高主要来自两个方面。首先，使用注意机制来生成潜在的有价值的元路径，而不需要预定义的元路径，这些元路径可能不是最好的。此外，使用非本地层来聚合来自远程节点的节点属性，这可能对目标节点很重要。综上所述，非局部聚合层可以显著提高模型的性能，而单位矩阵对于局部聚合层也非常重要。

在训练率分别为10%、20%、40%、60%和80%的情况下继续实验，结果如下表表4所示。可以看出，随着训练集百分比的增加，模型的分类准确率呈增加趋势。

6. 结论

在本文中，我们提出了一个新的框架，称为非局部信息聚合图神经网络(NLA-GNN)，可以更有效地探索异构图。具体来说，NLA-GNN由本地聚合层和非本地聚合层组成。局部聚合层从本地邻居中聚合节点属性，非局部聚合层利用注意力引导排序，从有价值的远程节点中聚合节点属性。因此有效地挖掘了局部和非局部信息。我们比较了NLA-GNN与不同的方法，包括传统的网络嵌入方法和图神经网络方法。实验结果表明，NLA-GNN具有较好的性能。此外，我们的消融研究结果验证了非局部聚集层对于提高NLAGNN性能的必要性。综上所述，通过非局部聚合，我们提出的方法可以更有效地利用异构图的结构信息来生成节点嵌入。实验结果表明，本文讨论的全局注意机制和一维卷积有效地捕获了远程节点依赖关系。然而，直接在大规模数据集上部署这种方法需要大量的内存来进行全局注意力提取，这对在小型机器上部署提出了挑战。因此，未来的考虑可能涉及现有远程节点依赖关系的分布式聚合，以便为大规模数据集扩展模型。

参考文献

[1] ：Siheng Wang, Guitao Cao, Wenming Cao, Yan Li. NLA-GNN: Non-local information aggregated graph neural network for heterogeneous graph embedding .[J] Pattern Recognition DOI:10.1016/j.patcog.2024.110940

[2] Dongyue Chen , Ruonan Liu , Qinghua Hu, and Steven X. Ding. Interaction-Aware Graph Neural Networks for Fault Diagnosis of Complex Industrial Processes. [J] IEEE TRANSACTIONS ON NEURAL NETWORKS AND LEARNING SYSTEMS, VOL. 34, NO. 9, SEPTEMBER 2023 DOI:10.1109/TNNLS.2021.3132376