探索利用人工智能追踪逃犯的新技术

news2024/10/10 13:52:23

介绍

论文地址：https://arxiv.org/abs/2404.12626
近年来，"追逃游戏 "引起了人们的广泛关注。"追逃游戏 "模拟了多组追捕者与单个逃犯之间的追捕游戏。这种博弈发生在城市道路网等图上，有效地找到这种博弈的策略具有多种潜在应用，包括在现实世界的城市安全中尽早逮捕罪犯。

然而，传统方法依赖于某些初始条件（如玩家的初始位置和入口/出口设置），由于这些条件在真实犯罪现场中不断变化，目前的算法每次都需要重新计算，效率低下。因此，本文提出了一个名为 "Grasper "的新框架。

Grasper 是一个多功能系统，可以根据初始条件生成跟踪器的策略。图神经网络将初始条件转换为嵌入向量，超网络则根据嵌入向量生成跟踪器的行为策略。此外，还开发了一种高效的三阶段学习程序和一种使用启发式方法得出的参考策略的新型预训练方法。

在对各种地图的实验中，Grasper 显示出了远远优于传统方法的性能和多功能性。即使初始条件发生变化，只需点击一下鼠标，就能生成针对具体情况的新策略，这种能力使 Grasper 成为一种创新的追逐和逃脱游戏解算器，在现实世界中具有巨大的应用潜力。

建议的方法（Grasper）

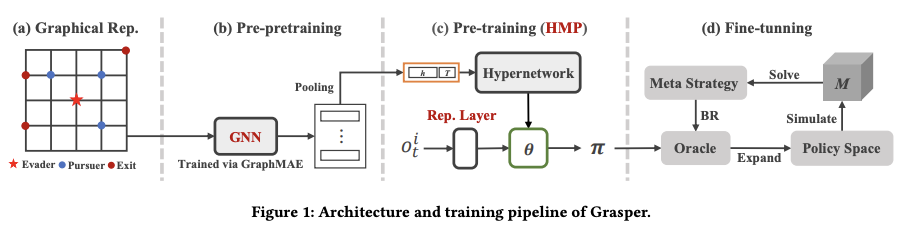
Grasper 是一个通用的追逐者策略生成框架，可用于追逐和逃脱游戏中的不同初始条件。其三个主要组成部分是

图神经网络（GNN）

追逃游戏的初始条件（如玩家的起始位置、入口和出口的位置）被嵌入到一个图中，然后将其输入到 GNN 中以获得隐藏状态向量（图 1(a) 和 (b)）。

超网络

以上述隐藏状态向量和时间跨度为输入，生成该游戏特有的跟踪器基本测量参数（图 1©）。

观测表示层

这一层将追踪器的观测数据（如播放器的位置）转换为嵌入向量。

Grasper 采用高效的三步学习程序

(1) 预学习：使用 GraphMAE 等自我监督方法从图形数据中预学习 GNN。
(2) 预学习：采用新颖的启发式多任务预学习（HMP）来学习超网络和观测表示层。利用启发式方法（如 Dijkstra 方法）得出的参考测量值对跟踪器测量值进行正则化，以提高搜索效率。
(3) 微调：在 PSRO 算法的每次迭代中，超网络生成的基本策略用于初始化，以微调跟踪器的最优响应策略。

因此，Grasper 将图表示法、超网络和高效学习程序结合在一起，成为解决追逐与逃脱游戏泛化问题的创新方法。

试验

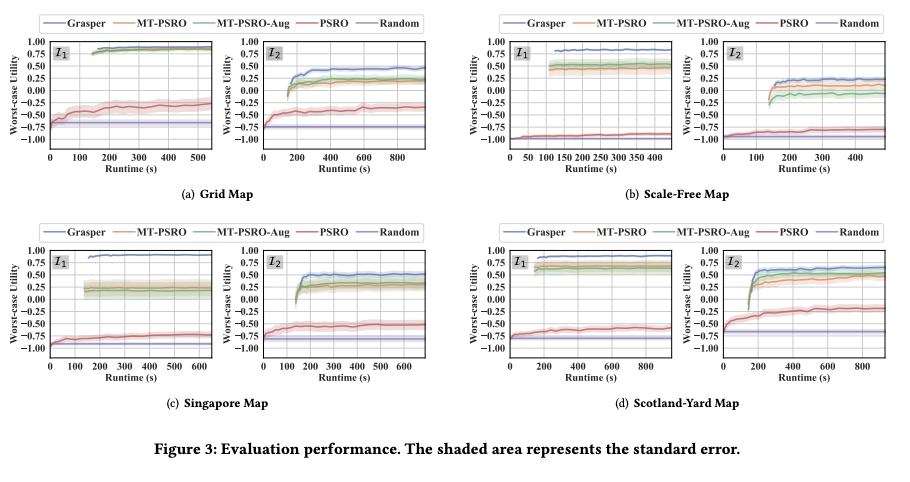图 3 比较了 Grasper 和传统方法的性能。纵轴表示跟踪器最坏情况下的效用值，横轴表示执行时间。
- 对于所有地图，Grasper 都比传统方法显示出更高的收敛值和更稳定的性能，即使在增加了预训练时间之后也是如此。
- 特别是，Grasper 的泛化性能在非分布测试集 (I2) 中表现突出。
- 从图中的斜率可以看出，Grasper 在 PSRO 的每次迭代中改进度量的速度都比传统方法快得多。

表 1 显示的结果证实了所提方法的关键组成部分：启发式引导的多任务预训练（HMP）和观察表示层（Rep.）的有效性。
- 可以看出，只有同时使用 HMP 和观察表示层时，才能获得较高的效用值和较小的标准偏差。
- 这说明这两种新方法都是必不可少的。

审议

- Grasper 的高性能和稳定性源于其能够根据初始条件输出跟踪测量值的结构特征。
- 特别是，Grasper 能够在初始条件不同的博弈中稳健地输出精确的解，而传统方法的性能则会明显下降。
- 由于高质量的初始化和快速的策略改进，即使增加了预训练时间，最终收敛时间也比传统方法更快。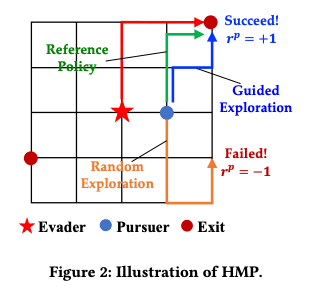- HMP 减少了随机搜索，提高了基于启发式搜索的效率（图 2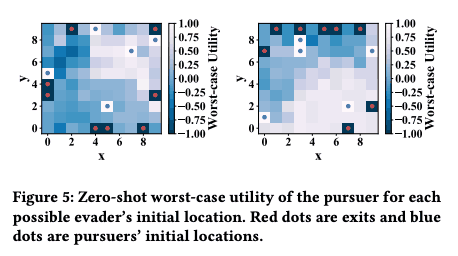）。- 此外，图 5 显示，Grasper 能够针对逃犯的不同初始位置输出合理的追捕效用值。