题一 扩展欧几里得算法

解题思路

原链接：https://www.acwing.com/solution/content/1393/（下同）

代码实现

#include<iostream>

using namespace std;

void exgcd(int a, int b, int &x, int &y)
{
    if(b == 0)
    {
        x = 1, y = 0;
        return ;
    }
    
    int x1, y1;//x1, y1是下一层循环时的x, y;
    
    exgcd(b, a % b, x1, y1);
    
    x = y1, y = x1 - a / b * y1;//我们需要考虑的是当前层的x, y的值，使得循环从深到浅结束时能得到当前层的x, y的值
    
    return ;
}

int main()
{
    int n, a, b;
    int x, y;
    
    cin >> n;
    
    while(n -- )
    {
        scanf("%d%d", &a, &b);
        exgcd(a, b, x, y);
        
        printf("%d %d\n", x, y);
    }
    return 0;
}

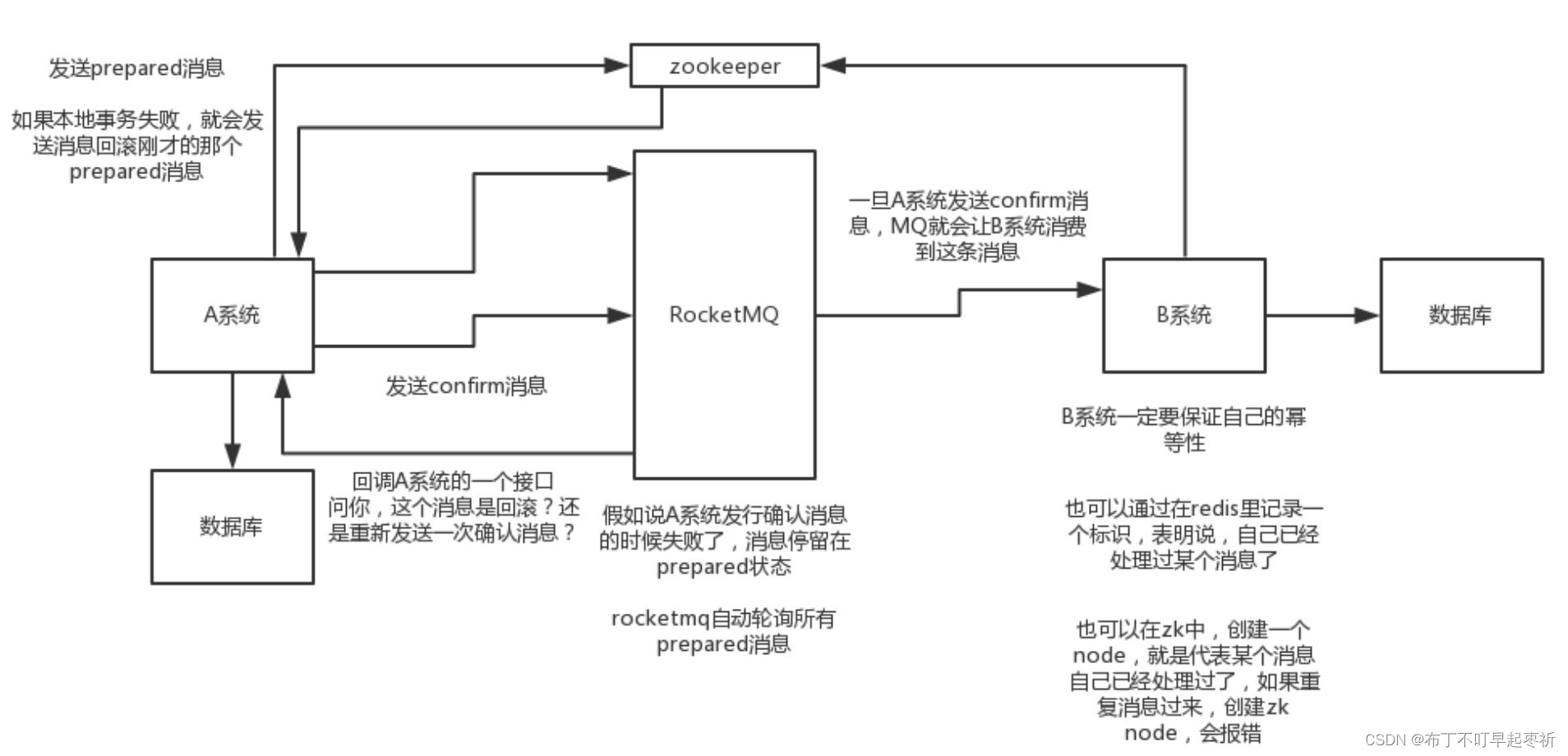
题二 线性同余方程

解题思路

注：图中\ *代表 *，表示乘法(LaTeX炸了)

具体思路

1. 因为 𝑎∗𝑥≡𝑏(𝑚𝑜𝑑 𝑚) 等价于𝑎∗𝑥−𝑏 是m的倍数，因此线性同余方程等价为 a∗x+m∗y=b;
2. 根据 Bezout 定理，上述等式有解当且仅当 gcd(a,m)|b;
3. 因此先用扩展欧几里得算法求出一组整数 x₀, y₀使得 a∗x₀+m∗y₀=gcd(a,m),再将x₀扩大b / gcd(a, m)倍即可;

代码实现

#include<iostream>

using namespace std;

int exgcd(int a, int b, int &x, int &y)
{
    if(b == 0)
    {
        x = 1, y = 0;
        return a;
    }
    
    int x1, y1, t;
    
    t = exgcd(b, a % b, x1, y1);
    x = y1, y = x1 - a / b * y1;
    
    return t;
}

int main()
{
    int n, a, b, m, x, y;
    
    cin >> n;
    
    while(n -- )
    {
        scanf("%d%d%d", &a, &b, &m);
        
        int d = exgcd(a, m, x, y);
        
        if(b % d != 0)
        {
            cout << "impossible" << endl;
        }
        else
        {
            x = (long long) x * b / d % m;
 //为什么要%m，为了符合题意输出int范围内的x
 //同时不违反题目给的条件  ai×xi≡bi(modmi)能推出ai×(xi%mi)≡bi(modmi)
            cout << x << endl;
        }
    }
    return 0;
}