目录

一，3309. 连接二进制表示可形成的最大数值

二，3310. 移除可疑的方法

三，3311. 构造符合图结构的二维矩阵

四，3312. 查询排序后的最大公约数

---

一，3309. 连接二进制表示可形成的最大数值

本题数据范围较小，可以使用递归枚举每一种排列方式，计算出最大值，代码如下：

class Solution {
    int ans = 0;
    public int maxGoodNumber(int[] nums) {
        dfs(0, "", nums);
        return ans;
    }
    void dfs(int i, String res, int[] nums){
        if(i == (1<<3)-1){
            ans = Math.max(ans, Integer.parseInt(res, 2));
            return;
        }
        for(int j=0; j<3; j++){
            if((i>>j&1)==1) continue;
            dfs(i|1<<j, res + Integer.toBinaryString(nums[j]), nums);
        }
        return ;
    }
}

但是该方式只适用于数据范围较小的题，下面介绍一种 O(nlogn) 的做法，我们先用十进制的方式来思考一下，给你一个数组 [9，10] ，如何使得这个数组用十进制并接得到的值更大？我们当然是比较一下：是9在前大，还是10在前大，然后决定这两个拼接的顺序。那么拓展到大小为 n 的数组如何决定它们的顺序？和上述做法一样，相邻的数依次比较，类似于冒泡排序。那么对于本题使用二进制拼接也是同理，代码如下：

class Solution {
    public int maxGoodNumber(int[] t) {
        Integer[] nums = new Integer[t.length];
        for(int i=0; i<t.length; i++)
            nums[i] = t[i];
        //注意要想按照自己的想法排序，必须使用Integer数组
        Arrays.sort(nums, (x, y)->{
            int len_x = Integer.toBinaryString(x).length();
            int len_y = Integer.toBinaryString(y).length();
            int xy = x << len_y | y;
            int yx = y << len_x | x;
            return yx - xy;
        });
        int ans = 0;
        for(int x : nums){
            int len = Integer.toBinaryString(x).length();
            ans = ans << len | x;
        }
        return ans;
    }
}

二，3310. 移除可疑的方法

本题题意给你一个可疑方法 k，如果被 k 直接调用/间接调用，那么这些方法也被视为可疑方法（注意：调用可疑方法的方法不是可疑方法），如果没有其他方法调用可疑方法，返回非可疑方法；否则，返回所用方法。

我们可以建立一个图，使用 dfs/bfs 找到所有的可疑方法，然后枚举 invocations 数组，比如每个元素为 [x，y]，如果 x 不是可疑方法 && y 是可疑方法，说明有非可疑方法调用可疑方法，返回所有方法；否则只返回非可疑方法。

代码如下：

class Solution {
    public List<Integer> remainingMethods(int n, int k, int[][] invocations) {
        List<Integer> ans = new ArrayList<>();
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, e->new ArrayList<>());
        for(int[] e : invocations){
            g[e[0]].add(e[1]);
        }
        Queue<Integer> que = new LinkedList<>();
        que.add(k);
        Set<Integer> set = new HashSet<>();
        set.add(k);
        while(!que.isEmpty()){
            int x = que.poll();
            for(int y : g[x]){
                if(!set.contains(y)){
                    que.add(y);
                    set.add(y);
                }
            }
        }
        for(int[] e : invocations){
            if(!set.contains(e[0]) && set.contains(e[1])){
                for(int i=0; i<n; i++)
                    ans.add(i);
                return ans;
            }
        }
        for(int i=0; i<n; i++){
            if(!set.contains(i))
                ans.add(i);
        }
        return ans;
    }
}

三，3311. 构造符合图结构的二维矩阵

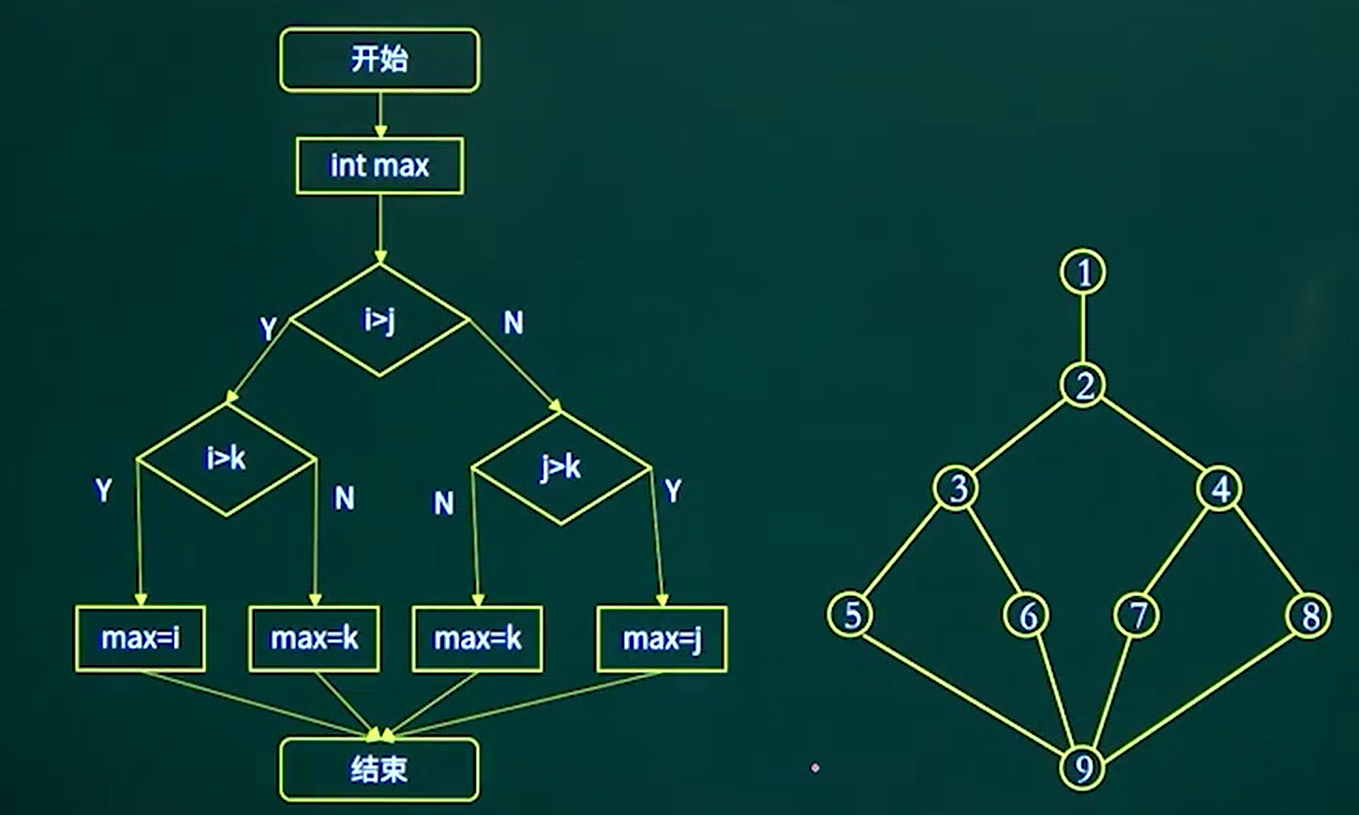
本题可以想象成拼拼图，我们可以先找到四个角落的点（如果行列>=3，那么它只有两个相邻的点），然后不断的往里拼，但是本题不知道四个角的对应位置，所以我们可以先找到一个角洛的点，然后往一边拼，注意一个边上点（除了角落的点），它们相邻的点有三个，不断的填充，直到找到一个这条边的另一个角落（即只有两个相邻点的点），这样我们就拼出一个边了，然后通过这个边不断的往下拼就行了。

上述是行列>=3的情况，如果它只有一行/列，那么它所有点中最少的相邻点必须为1，所以只需要判断最少的相邻是否为1，就直到是否是一行/列。

如果它只有两行/列，那么只需要判断所有点中最多的相邻点是否为4，如果不为4且不是一行/列，说明它只用两行/列。

代码如下：

class Solution {
    public int[][] constructGridLayout(int n, int[][] edges) {
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, e->new ArrayList<>());
        for(int[] e : edges){
            g[e[0]].add(e[1]);
            g[e[1]].add(e[0]);
        }
        int[] node = new int[5];
        Arrays.fill(node, -1);
        for(int x=0; x<n; x++){
            node[g[x].size()] = x;
        }
        List<Integer> row = new ArrayList<>();
        if(node[1] != -1){
            row.add(node[1]);
        }else if(node[4]==-1){
            int x = node[2];
            for(int y : g[x]){
                if(g[y].size() == 2){
                    row.add(x);
                    row.add(y);
                    break;
                }
            }
        }else{
            int x = node[2];
            row.add(x);
            int pre = x;
            x = g[x].get(0);
            while(g[x].size() == 3){
                row.add(x);
                for(int y : g[x]){
                    if(y != pre && g[y].size() < 4){
                        pre = x;
                        x = y;
                        break;
                    }
                }
            }
            row.add(x);
        }
        int k = row.size();
        int[][] ans = new int[n/k][k];
        boolean[] vis = new boolean[n];
        for(int j=0; j<k; j++){//把第一行放进去
            int x = row.get(j);
            ans[0][j] = x;
            vis[x] = true;
        }
        for(int i=1; i<ans.length; i++){
            for(int j=0; j<k; j++){
                for(int y : g[ans[i-1][j]]){
                    if(!vis[y]){
                        vis[y] = true;
                        ans[i][j] = y;
                        break;
                    }
                }
            }
        }
        return ans;
    }
}

四，3312. 查询排序后的最大公约数

本题最重要的部分就是计算出每个 gcd 出现的次数，对于查询，我们可以使用二分前缀和的方式算出答案。

如何计算每个 gcd 出现的次数？假设要计算 gcd 等于 2 出现的次数，比如说有 n 个 2 的倍数，那么我们可以得到 Cn2 个数对（即 (n-1)*n/2 ），但是这么多数对，不一定每一个 gcd 的值都为 2，比如 4 和 8 的 gcd 就为 4，6 和 12 的 gcd 就为 6，所以我们需要从 (n-1)*n/2 个数对中减去数对的 gcd 为 4，6，8，....。这样就能得到 gcd 为 2 的数对个数了。

定义 cntGcd[i] 表示 gcd 为 i 的数对的个数，cntGcd[i] = (n-1)*n/2 - cntGcd[2*i] - cntGcd[3*i] - ...，从上述公式可以看出，要想计算出 cntGcd[i]，必须先计算出 cntGcd[2*i]、cntGcd[3*i]，所以我们需要从后往前遍历。

代码如下：

class Solution {
    //cnt[2] = C(n,2) - cnt[4] - cnt[6] - ...
    public int[] gcdValues(int[] nums, long[] queries) {
        int[] cntX = new int[50001];
        int mx = 0;
        for(int x : nums){
            cntX[x]++;
            mx = Math.max(mx, x);
        } 
        long[] cnt = new long[mx+1];
        for(int i=mx; i>=1; i--){
            int s = 0;
            for(int j=i; j<mx+1; j+=i){
                s += cntX[j];
                cnt[i] -= cnt[j]; //去除2i,3i,4i...（虽然j从i开始，但是cnt[i]初始值为0，所以实际上没有减去i）
                //为什么不是从2*i开始？因为要计算i的倍数的和s，如果从2i开始会少计算i出现的个数！！
            }
            cnt[i] += (long)(s - 1) * s / 2;
        }
        for(int i=1; i<mx+1; i++){
            cnt[i] += cnt[i-1]; 
        }
        int[] ans = new int[queries.length];
        for(int i=0; i<queries.length; i++){
            int l = 1, r = mx;
            while(l <= r){
                int mid = (l + r) / 2;
                if(cnt[mid] <= queries[i]){
                    //为什么加=？因为query[i]可以取到0（当然也可以写成cnt[mid]-1 < queries[i]）
                    l = mid + 1;
                }else{
                    r = mid - 1;
                }
            }
            ans[i] = l;
        }
        return ans;
    }
}