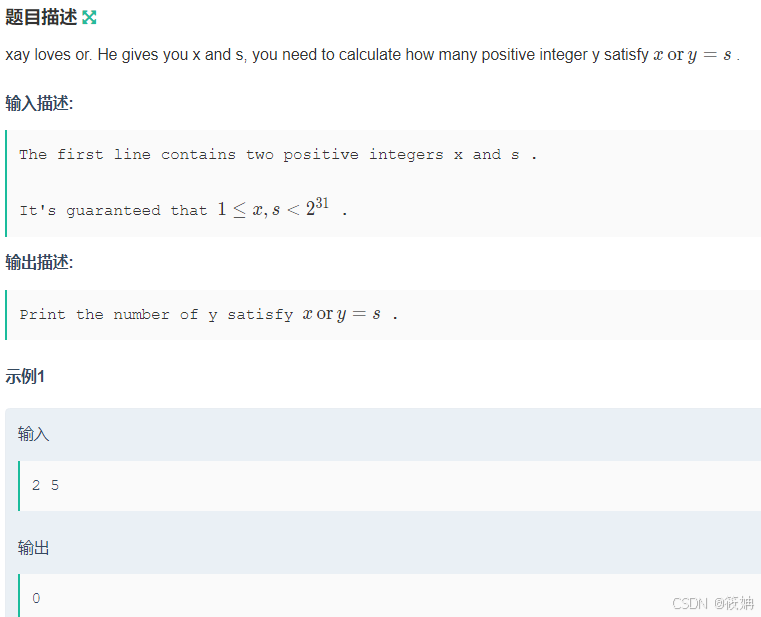
xay loves or
题目描述
登录—专业IT笔试面试备考平台_牛客网
运行思路
题目要求我们计算有多少个正整数 yy 满足条件 x \text{ OR } y = sx OR y=s。这里的“OR”是指按位或运算。为了理解这个问题,我们需要考虑按位或运算的性质。
对于任意两个位 a_iai 和 b_ibi(a_i, b_i \in \{0, 1\}ai,bi∈{0,1}),按位或运算的结果 c_ici 为:
- 如果 a_i = 0ai=0 且 b_i = 0bi=0,那么 c_i = 0ci=0。
- 否则,c_i = 1ci=1。
因此,如果 x \text{ OR } y = sx OR y=s,那么对于 ss 中每一位为 1 的位置,xx 或 yy 在对应位置至少有一个 1;对于 ss 中每一位为 0 的位置,xx 和 yy 在对应位置都必须是 0。
- 对于 ss 中每一位为 0 的位置,如果 xx 在该位置也是 0,则 yy 在该位置也必须是 0,否则无法满足 x \text{ OR } y = sx OR y=s。
- 对于 ss 中每一位为 1 的位置,如果 xx 在该位置是 0,则 yy 在该位置可以是 0 或 1;如果 xx 在该位置是 1,则 yy 在该位置可以是 0 或 1,因为 xx 已经确保了结果位为 1。
运行代码
#include <iostream>
#include <bitset>
#include<math.h>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int x, s;
cin >> x >> s;
if ((s & x) == x) {
cout << int(pow(2, __builtin_popcount(x))) - (x == s) << "\n";
} else {
cout << 0 << "\n";
}
return 0;
}
代码思路
-
输入读取:首先,我们读取两个整数
x和s。 -
条件判断:检查
s & x是否等于x。如果s & x != x,说明s中有些位为 0 而x中对应位为 1,这是不可能的,因为x OR y的结果在这些位上必须是 1。因此,直接输出 0。 -
计算符合条件的
y数量:- 如果
s & x == x,说明x中为 1 的位在s中也必须是 1。接下来,我们需要计算s中为 1 而x中为 0 的位的数量。 - 使用
__builtin_popcount(s & ~x)计算这些位的数量。 - 每个这样的位可以自由选择 0 或 1,因此符合条件的
y的数量是2的这些位的数量次方。 - 由于
y必须是正整数,我们需要减去y = 0的情况。当x == s时,y = 0是唯一的情况,因此需要减去 1。
- 如果
__builtin_popcount
函数描述
__builtin_popcount 是 GCC 编译器提供的一组内置函数之一,用于计算一个整数的二进制表示中 1 的个数。具体来说,__builtin_popcount 接受一个无符号整数作为参数,并返回该整数的二进制表示中 1 的个数。
举例:假设有一个整数 x = 5,其二进制表示为 101。调用 __builtin_popcount(5) 将返回 2,因为 101 中有两个 1。
语法:
int __builtin_popcount(unsigned int x);使用场景
在上述代码中,__builtin_popcount 用于计算 s & ~x 中 1 的个数。具体来说:
~x是x的按位取反。s & ~x表示s中为 1 而x中为 0 的位。__builtin_popcount(s & ~x)计算这些位的数量。
代码示例
#include <iostream>
#include <bitset>
int main() {
unsigned int x = 5; // 二进制表示为 101
unsigned int s = 7; // 二进制表示为 111
unsigned int result = s & ~x; // 111 & ~101 = 111 & 010 = 010
int count = __builtin_popcount(result); // 010 中有 1 个 1
std::cout << "Result: " << std::bitset<8>(result) << ", Count: " << count << std::endl;
return 0;
}输出
Result: 00000010, Count: 1