- 目的:让大家能够在 AI-NLP 领域由基础到入门
- 具体安排:
- NLP介绍 + 文本预处理
- RNN 及其变体(涉及案例)
- Transformer 原理详解
- 迁移学习 和 Bert 模型详解 (涉及案例)
- 特点:
- 原理 + 实践
- 每个文章会有练习代码
- 注意: 部分知识原理需要反复的回顾,如有必要,需要自己进行手动推导
- 要求:
- 建议每次看完文档,自己完成代码。
- 因为内容过多,我们的扩展内容,和课程无关紧要内容,建议在 学完NLP之后弄,我们已经设置了最短路径入门,否则枝叶过多,容易走岔了。
- 本系列文章将开启你的NLP之旅,全面从企业实战角度出发,内容结合当下时代背景,更多关注NLP在深度学习领域的进展,这也将是未来几年甚至几十年NLP的重要发展方向。内容对应企业开发标准流程和企业发展路径,助力你成为一名真正的AI-NLP工程师。
-

【NLP自然语言处理】01-基础学习路径简介
news2026/2/14 11:24:58
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/2195832.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Nat. Commun.:飞秒激光书写受蚂蚁启发的可重构微型机器人集体
背景介绍生物在各种环境中的集体行为十分普遍,它们能够自发有序地完成单个个体难以完成的任务。目前,生物集体的形成主要分为两大类。第一类生物个体之间没有直接接触,如蜜蜂、鱼和鸟类,这导致这些集体不稳定,容易受到…
Ubuntu24 Firefox和Window Firefox同步问题
由于平常开发在Ubuntu系统,但是日常学习查资料又在Window系统,查资料保存网页到浏览器中时,经常遇到两个平台标签同步问题,希望可以选一个支持Ubuntu、Window的浏览器。
选用Google Chrome浏览器,确实挺好用ÿ…
微服务seata解析部署使用全流程
官网地址: Seata 是什么? | Apache Seata
1、Seata术语
用来管理分布式事务,由阿里巴巴出品。
【1、TC (Transaction Coordinator) - 事务协调者】
用来维护事务的,包括主事务和分支事务。
【2、TM (Transaction Manager) - …
TCP与UDP协议(三次握手四次挥手)
TCP与UDP 简介TCP和UDP一、TCP1.1 TCP的三次握手问题来了:为啥是三次握手而不是两次呢? 1.2建立连接后的通信过程(丢包与乱序问题)1.3四次挥手问题来了:为什么要四次挥手? 二、UDP 简介TCP和UDP
TCP、UDP都…
机器学习笔记(持续更新)
重复值处理: 重复值处理代码:
import pandas as pd
data pd.DataFrame({学号: [1, 2, 3, 4, 5, 6, 7, 7, 8],身高: [172,162,175,170,168,160,164,164,160],体重: [70,62,75,68,67,58,64,64,53]
})
data.drop_duplicates([学号], keep last, inplaceT…
SQL第13课挑战题
1. 使用inner join,以检索每个顾客的名称(customers表中的cust_name)和所有的订单号(orders表中的order_num). 2. 修改第一题,仅列出所有顾客,及时他们没有下过订单。 3. 使用outer join联结products表和or…
【Easy RL】Easy RL蘑菇书全书学习笔记
【Easy RL】Easy RL蘑菇书全书学习笔记 第一章 强化学习基础1.1 强化学习概述监督学习强化学习与监督学习的不同之处二者的区别总结强化学习的特征强化学习的优越性预演(rollout)和 轨迹(trajectory)的概念端到端的概念深度强化学…
BurpSuite内置浏览器打不开(实用解决法/简便)
也不知道出现了什么问题就是莫名其妙的内置浏览器打不开,有时候不想配置代理很麻烦,这里实用的解决办法. 任务一 报错情况(反正也看不懂) 任务二 我们先去尝试打开这个运行模式,然后我们再去重试,如果还是打…
【重学 MySQL】五十九、二进制字符串类型与 JSON 类型
【重学 MySQL】五十九、二进制字符串类型与 JSON 类型 二进制字符串类型JSON类型 在MySQL数据库中,二进制字符串类型与JSON类型各自具有独特的特点和用途。
二进制字符串类型
二进制字符串类型在MySQL中主要用于存储二进制数据。这类数据类型包括BINARY、VARBINAR…
使用 ChatGPT Canvas 辅助 ABAP 开发
ChatGPT Canvas 是最近 OpenAI 推出的一个新功能,它不仅仅是一个简单的聊天对话式窗口。
Canvas 旨在扩展 ChatGPT 平台的功能,超越简单的问答交互。
Canvas 可以在单独的窗口中打开专用工作区,用户能够更直观、更高效地与 ChatGPT 在复杂的写作或者编码项目进行协作。
有…
Nginx08-反向代理
零、文章目录
Nginx08-反向代理
1、概述 关于正向代理和反向代理,我们在前面已经介绍过了,简而言之就是正向代理代理的对象是客户端,反向代理代理的是服务端,这是两者之间最大的区别。 Nginx即可以实现正向代理,也可…
【Unity】版本不一致且未升级资产,导致 Unity Sprite 2D 动画播放错误
自己的 Unity版本是 2022.3.45f1。目前折腾的这插件 2D Action RPG Engine: Mythril2D ,推荐使用的 Unity 版本是 2021.3.18。
倒腾了这个 unity animation 动画半天,发现这个 animation sprite resolver 在导入动画帧的时候,一直都导入的是…
LeetCode 11 Container with Most Water 解题思路和python代码
题目: You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the co…
【论文阅读】AUTOREGRESSIVE ACTION SEQUENCE LEARNING FOR ROBOTIC MANIPULATION
ABSTRACT
自回归模型在自然语言处理中取得了显著的成功。在这项工作中,我们为机器人操纵任务设计了一个简单而有效的自回归架构。我们提出了Chunking Causal Transformer(cct),它扩展了因果关系transformers的下一个单标记预测 n…
Nginx07-静态资源访问
零、文章目录
Nginx07-静态资源访问
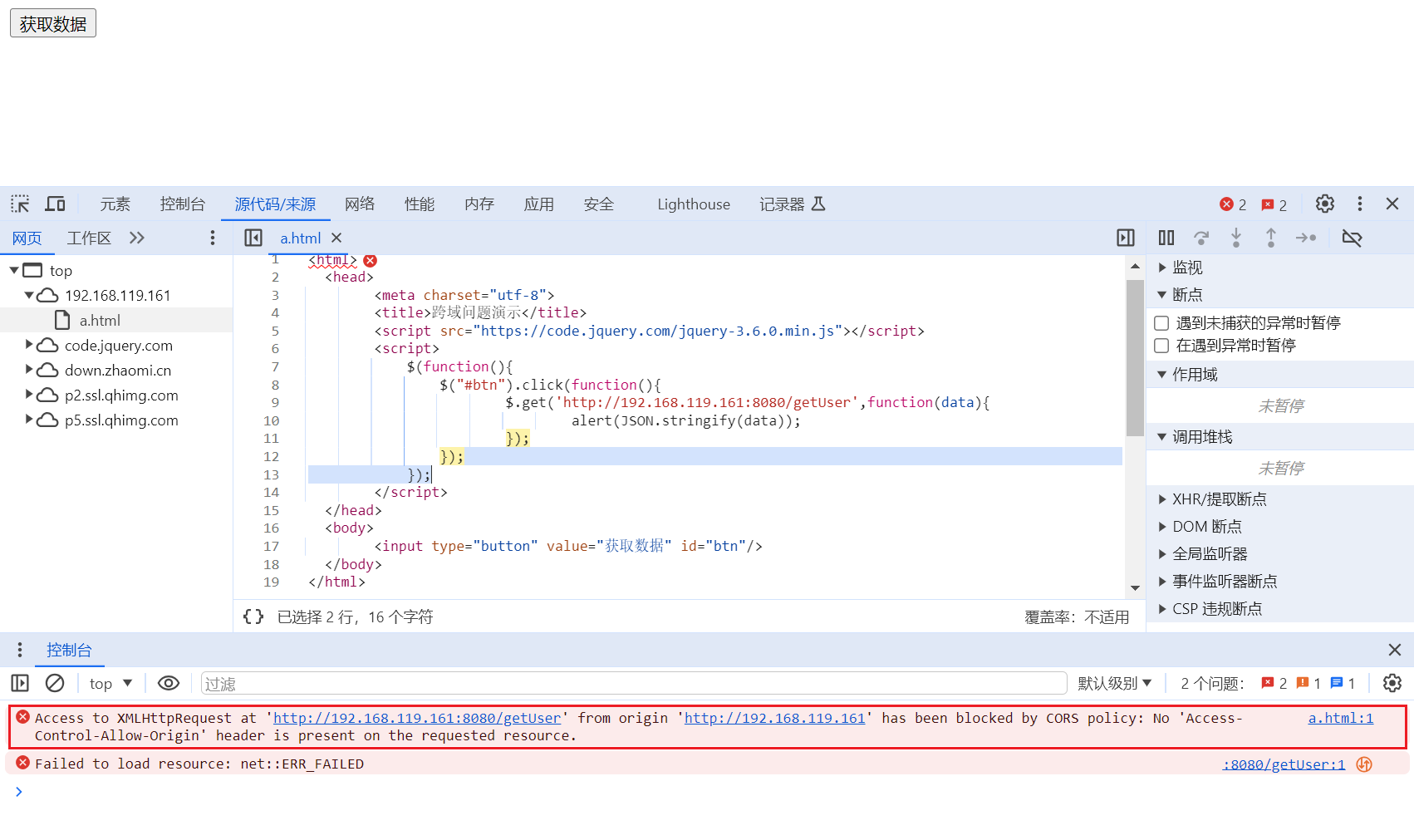
1、Nginx解决跨域问题
(1)同源策略
同源策略(Same-Origin Policy)是一个关键的网络安全概念,由Netscape公司在1995年引入,现在被所有现代浏览器所采用。它限制了从一…
基于JAVA的鲜花商城管理系统(源码+定制+讲解)鲜花商城管理系统、鲜花商城管理平台、鲜花商城信息管理、鲜花商城系统开发与应用、鲜花在线商城管理系统
博主介绍: ✌我是阿龙,一名专注于Java技术领域的程序员,全网拥有10W粉丝。作为CSDN特邀作者、博客专家、新星计划导师,我在计算机毕业设计开发方面积累了丰富的经验。同时,我也是掘金、华为云、阿里云、InfoQ等平台…
毕业设计项目 深度学习安全帽佩戴检测(源码+论文)
文章目录 0 前言1 项目运行效果2 设计概要3 最后 0 前言
🔥这两年开始毕业设计和毕业答辩的要求和难度不断提升,传统的毕设题目缺少创新和亮点,往往达不到毕业答辩的要求,这两年不断有学弟学妹告诉学长自己做的项目系统达不到老师…
sqli-labs靶场第二关less-2
sqli-labs靶场第二关less-2
本次测试在虚拟机搭建靶场,从主机测试
1、输入?id1和?id2发现有不同的页面回显
2、判断注入类型 http://192.168.128.3/sq/Less-2/?id1’ 从回显判断多一个‘ ,预测可能是数字型注入 输入 http://192.168.128.3/sq/Less…
Sharding 分页原理分析
优质博文:IT-BLOG-CN
如果业务上需要执行如下分页查询,Sharding-JDBC如何执行分页查询的? 官方文档
select * from student_time ORDER BY create_time ASC limit 1000, 5;Sharding-JDBC分页查询时在每个分表中都查询1005条数据,…
【树结构与栈】中等力扣练习题
二叉树中和为目标值的路径
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。叶子节点 是指没有子节点的节点。
示例 1: 输入:root [5,4,8,11,null,13,4,7,2,null,null,5…