详解三种常用标准化：Batch Norm Layer Norm RMSNorm

news2024/10/9 16:32:42

Normalization

Normalization现在已经成了神经网络中不可缺少的一个重要模块了，并且存在多种不同版本的归一化方法，其本质都是减去均值除以方差，进行线性映射后，使得数据满足某个稳定分布，如下图所示：
在这里插入图片描述

深度学习中，归一化是常用的稳定训练的手段，CV 中常用 Batch Norm； Transformer 类模型中常用 layer norm，而 RMSNorm 是近期很流行的 LaMMa 模型使用的标准化方法，它是 Layer Norm 的一个变体。值得注意的是，这里所谓的归一化严格讲应该称为标准化Standardization ，有时也称为白化whitening。它描述一种把样本调整到均值为 0，方差为 1 的缩放平移操作。使用这种方法可以消除输入数据的量纲，有利于随机初始化的网络训练。
本文将对BatchNorm、LayerNorm、RMSNorm三种归一化进行介绍。详细讨论前，先粗略看一下 Batch Norm 和 Layer Norm 的区别
在这里插入图片描述

BatchNorm是对整个 batch 样本内的每个特征做归一化，这消除了不同特征之间的大小关系，但是保留了不同样本间的大小关系。BatchNorm 适用于 CV 领域，这时输入尺寸为 b × c × h × w b\times c\times h\times wb×c×h×w (批量大小x通道x长x宽)，图像的每个通道 c cc 看作一个特征，BN 可以把各通道特征图的数量级调整到差不多，同时保持不同图片相同通道特征图间的相对大小关系
LayerNorm是对每个样本的所有特征做归一化，这消除了不同样本间的大小关系，但是保留了一个样本内不同特征之间的大小关系。LayerNorm 适用于 NLP 领域，这时输入尺寸为 b × l × d (批量大小x序列长度x嵌入维度)，如下图所示：

注意这时长 l 的 token 序列中，每个 token 对应一个长为 d 的特征向量，LayerNorm 会对各个 token 执行 l 次归一化计算，保留每个 token d 维嵌入内部的相对大小关系，同时拉近了不同 token 对应特征向量间的距离。与之相比，BN 会消除 d 维特征向量各维度之间的大小关系，破坏了 token 的特征（以下第 2 节会进一步说明这一点）

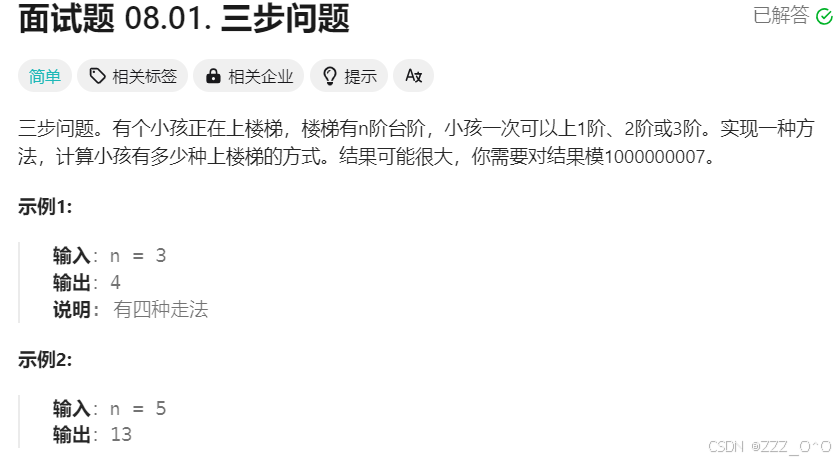
1. Batch Normalization

BN 对同一 batch 内同一通道的所有数据进行归一化，设输入的 batch data 为 x，BN 运算如下
在这里插入图片描述

注意我们在方差估计值中添加一个小的常量 ϵ (防除零因子)，以确保我们永远不会尝试除以零。

BatchNorm是一种在深度学习训练中广泛使用的归一化技术，有很多好处，包括正则化效应、减少过拟合、减少对权重初始值的依赖、允许使用更高的学习率等
示例代码参考自《动手学深度学习》7.5 节，适用于全连接层和卷积层，训练过程中使用滑动平均法计算 batch 数据的均值和方差；评估过程中使用最新的均值和方差结果

class BatchNorm(nn.Module):
    # num_features：完全连接层的输出数量或卷积层的输出通道数。
    def __init__(self, num_features, num_dims):
        super().__init__()
        if num_dims == 2: # 全连接层
            shape = (1, num_features)
        else:             # 卷积层
            shape = (1, num_features, 1, 1)
        
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def batch_norm(self, X, gamma, beta, moving_mean, moving_var, eps, momentum):
        if not torch.is_grad_enabled():
            # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
            X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
        else:
            assert len(X.shape) in (2, 4)
            if len(X.shape) == 2:
                # 使用全连接层的情况，计算特征维上的均值和方差
                mean = X.mean(dim=0)                                       # (num_features,)
                var = ((X - mean) ** 2).mean(dim=0)                        # (num_features,)
            else:
                # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。
                mean = X.mean(dim=(0, 2, 3), keepdim=True)                # (1,num_features,1,1) 保持X的形状，以便后面可以做广播运算
                var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True) # (1,num_features,1,1)
                
            # 训练模式下，用当前的均值和方差做标准化
            X_hat = (X - mean) / torch.sqrt(var + eps)
            
            # 更新移动平均的均值和方差
            moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
            moving_var = momentum * moving_var + (1.0 - momentum) * var
            
        Y = gamma * X_hat + beta  # 缩放和移位
        return Y, moving_mean.data, moving_var.data

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var，复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
       
        # 保存更新过的moving_mean和moving_var
        Y, self.moving_mean, self.moving_var = self.batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9
        )
        return Y

2. Layer Normalization

LN 主要用于 NLP 领域，它对每个 token 的特征向量进行归一化计算。LN 运算如下在这里插入图片描述

给定一个长 l 的句子，LN 要进行 l 次归一化计算，之后对每个特征维度施加统一的拉伸和偏移，如下图所示：

为什么 LN 比 BN 更适用于 Transformer 类模型呢，这是因为 transformer 模型是基于相似度的，把序列中的每个 token 的特征向量进行归一化有利于模型学习语义，第一步调整均值方差时，相当于对把各个 token 的特征向量缩放到统一的尺度，第二步施加 γ , β 时，相当于对所有 token 的特征向量进行了统一的 transfer，这不会破坏 token 特征向量间的相对角度，因此不会破坏学到的语义信息。与之相对的，BN 沿着特征维度进行归一化，这时对序列中各个 token 施加的 transfer 是不同的，破坏了 token 特征向量间的相对角度关系

3. RMSNorm

RMSNorm 是 LayerNorm 的一个简单变体，来自 2019 年的论文 Root Mean Square Layer Normalization，被 T5 和当前流行 lamma 模型所使用。其提出的动机是 LayerNorm 运算量比较大，所提出的RMSNorm 性能和 LayerNorm 相当，但是可以节省7%到64%的运算
RMSNorm和LayerNorm的主要区别在于RMSNorm不需要同时计算均值和方差两个统计量，而只需要计算均方根 Root Mean Square 这一个统计量，公式如下在这里插入图片描述
论文 Do Transformer Modifications Transfer Across Implementations and Applications? 中做了比较充分的对比实验，显示出RMS Norm的优越性。一个直观的猜测是，计算均值所代表的 center 操作类似于全连接层的 bias 项，储存到的是关于预训练任务的一种先验分布信息，而把这种先验分布信息直接储存在模型中，反而可能会导致模型的迁移能力下降
下面给出 Transformer Lamma 源码中实现的 RMSNorm

class LlamaRMSNorm(nn.Module):
    def __init__(self, hidden_size, eps=1e-6):
        """
        LlamaRMSNorm is equivalent to T5LayerNorm
        """
        super().__init__()
        self.weight = nn.Parameter(torch.ones(hidden_size))
        self.variance_epsilon = eps

    def forward(self, hidden_states):
        input_dtype = hidden_states.dtype
        hidden_states = hidden_states.to(torch.float32)
        variance = hidden_states.pow(2).mean(-1, keepdim=True)
        hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon)
        return self.weight * hidden_states.to(input_dtype)