DAY26||669.修建二叉树 |108.将有序数组转换为二叉搜索树|538.把二叉搜索树转换为累加树

news2024/10/10 2:22:58

669.修剪二叉树

题目：669. 修剪二叉搜索树 - 力扣（LeetCode）

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：
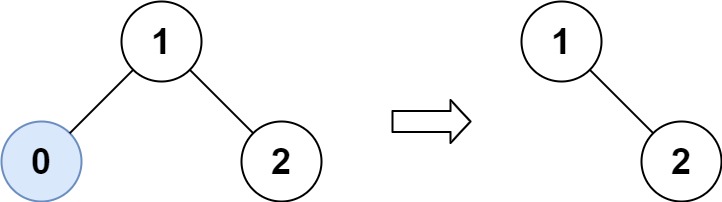
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]
示例 2：
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

思路：一层层往下遍历（递归当然返回是下一层返回给上一层，前序遍历的写法，中节点的处理逻辑就是查看是否在区间内，如果不是，就继续往下找，左子树遇到删除节点的从右子树找补上的节点，为什么不找左子树因为当前删除节点已经不在区间了，那么左子树的值比它小，不理会就行了（其实删除节点的时候就不要了，补上的树分支已经不一样了）右子树同理。

所以递归代码挺简洁的，模拟走一遍流程就能明白了。

递归

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(root==NULL)return NULL;
        
        if(root->val<low)return trimBST(root->right,low,high);//中，在左区间外的，继续遍历右子树找到值补上位置并返回上一层，右区间外的也一样
        if(root->val>high)return trimBST(root->left,low,high);

        root->left=trimBST(root->left,low,high);//左
        root->right=trimBST(root->right,low,high);//右

        return root;



    }
};

迭代

在剪枝的时候，可以分为三步：

将root移动到[L, R] 范围内，注意是左闭右闭区间
剪枝左子树
剪枝右子树

就是找到范围的root，定义cur指针再分别遍历修剪左右子树，修剪逻辑同递归写法。

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(!root)return nullptr;
        while(root!=nullptr&&(root->val<low||root->val>high))//找到在区间内的根节点
        {
            if(root->val<low)root=root->right;
            else root=root->left;
        }
        TreeNode*cur=root;
        while(cur)//修剪左子树
        {
            while(cur->left&&cur->left->val<low)
            cur->left=cur->left->right;
            cur=cur->left;//指针指向下一个
        }

        cur=root;//修剪右子树
        while(cur)
        {
            while(cur->right&&cur->right->val>high)
            cur->right=cur->right->left;
            cur=cur->right;
        }
        return root;

    }
};

108.将有序数组转换为二叉搜索树

题目：108. 将有序数组转换为二叉搜索树 - 力扣（LeetCode）

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。

示例:

前提：

平衡二叉树（Balanced Binary Tree）是一种特殊的二叉树，它在结构上保持一定的平衡性，以确保操作的效率较高。最常见的平衡二叉树类型是AVL树和红黑树。平衡的定义通常是指树中任意节点的两个子树的高度差不能超过一定的限制。对于AVL树，这个限制是1。

具体特点：

AVL树：对于每个节点，左子树和右子树的高度差（也称为平衡因子）不能超过1。AVL树的插入、删除和查找操作的时间复杂度都为O(log n)。
红黑树：这是一种弱平衡的二叉搜索树，确保最长路径不会超过最短路径的两倍，从而保证O(log n)的操作时间复杂度。

递归

class Solution {
    TreeNode*traversal(vector<int>& nums,int left,int right)
    {
        if(left>right)return nullptr;

        int mid=left+((right-left)/2);//相当于如果数组是偶数而中间值有两个时，取左边的做分割点
        TreeNode*root=new TreeNode(nums[mid]);
        root->left=traversal(nums,left,mid-1);
        root->right=traversal(nums,mid+1,right);
        return root;
    }
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        //分而治之，分割左右数组,和构建二叉树相似
        TreeNode*root=traversal(nums,0,nums.size()-1);
        return root;

    }
};

迭代法可以通过三个队列来模拟，一个队列放遍历的节点，一个队列放左区间下标，一个队列放右区间下标。但跳过了这个写法。。。待补

538.把二叉搜索树转换为累加树

题目：538. 把二叉搜索树转换为累加树 - 力扣（LeetCode）

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。节点的右子树仅包含键大于节点键的节点。左右子树也必须是二叉搜索树。

示例 1：

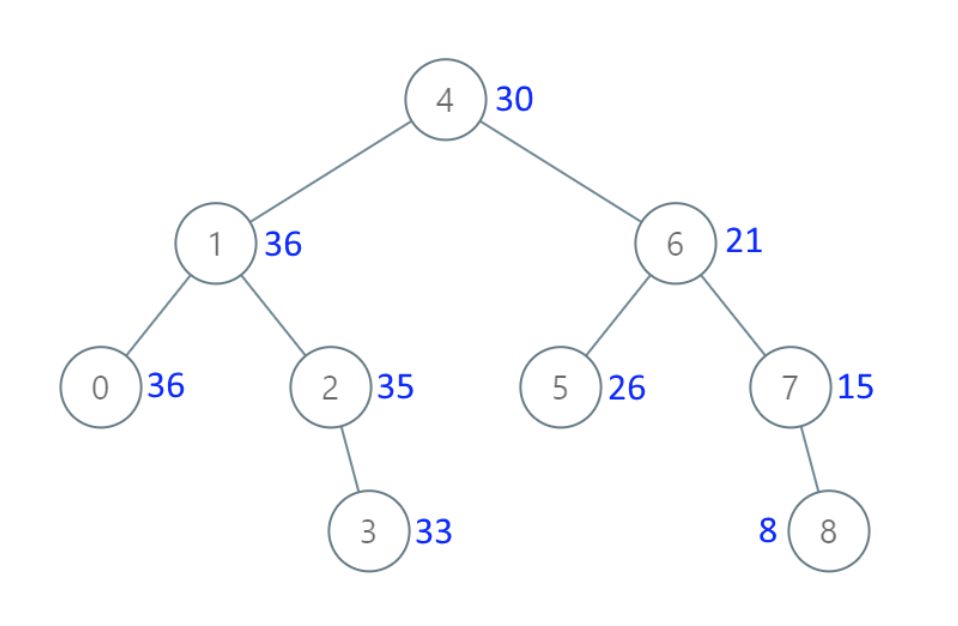
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 104 之间。
每个节点的值介于 -104 和 104 之间。
树中的所有值互不相同。
给定的树为二叉搜索树。

思路：

题目太长差点没看懂，其实就是更新后的每一个节点是所有比它大于或等于的值的和。本题适合的遍历顺序是后中前，然后类似双指针法，cur的值只要累加pre就行，然后pre跟随cur的步伐移动。

递归法

反中序遍历。

class Solution {
    int pre=0;
    private:
    void traversal(TreeNode*cur)
    {
        if(cur==nullptr)return;
        traversal(cur->right);//右

        cur->val+=pre;//中，累加前一个数的值
        pre=cur->val;

        traversal(cur->left); //作       
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        pre=0;
        traversal(root);
        return root;

    }
};

迭代法

模拟这个过程，模板题。

统一迭代法的一种。

栈模拟反中序遍历过程。

class Solution {
    private:
    int pre;
    void traversal(TreeNode*root)
    {
        stack<TreeNode*>st;//注意这里入栈的是指针
        TreeNode*cur=root; 
        while(cur!=NULL||!st.empty())   
        {
            if(cur!=NULL)
            {
                st.push(cur);//右
                cur=cur->right;
            }
            else
            {
                cur=st.top();
                st.pop();
                cur->val+=pre;//中
                pre=cur->val;

                cur=cur->left;//左

            }
        }
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        pre=0;
        traversal(root);
        return root;

    }
};

二叉树完结撒花，总体来说不是很难，但是熟练掌握程度还得看自己是否能独立做出来了。