数理统计（第1章第2节：一些常用的抽样分布）

news2025/11/3 22:35:39

目录

统计量的概率分布称为“抽样分布”

1. 正态母体的子样平均数的抽样分布

正态分布

 2. 卡方分布

3. t分布

4. F分布 

5. 例题

6. 总结 

统计量的概率分布称为“抽样分布”

1. 正态母体的子样平均数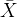\bar{X}的抽样分布

正态分布

        若随机变量X的概率密度为：

        f(x)=\frac{1}{\sqrt{2\pi}\sigma }e^{-\frac{(x-\mu )^2}{2\sigma^2}}

        则称X服从参数为\mu和\sigma^2的正态分布，X\sim N(\mu,\sigma^2),若\mu=0,sigma^2=1,则称X服从标准正态分布，X\sim N(0,1)

        性质：

        所以由此可得子样平均数 \bar{X}=\frac{1}{n}\sum_{i=1}^n x_i服从正态分布N(\mu,\frac{\sigma^2}{n}) 

        标准正态分布的\alpha上侧 分位数

        一般定义：设随机变量X的概率密度函数为f(x),对于任意给定的\alpha(0<\alpha<1),若存在x_{\alpha},使得 p\begin{Bmatrix} X\geq X_{\alpha} \end{Bmatrix} = \alpha \Leftrightarrow \int_{X_{\alpha}}^{+\infty }f(x)dx = \alpha,则称点X_{\alpha}为该概率分布的\alpha上侧分位数的上侧分为点

 例子：

 2. 卡方分布\chi ^2

        

 

 

3. t分布

 

 

4. F分布 

5. 例题

6. 总结 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2193516.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

[C#]winform部署官方yolov11-obb旋转框检测的onnx模型

[C#]winform部署官方yolov11-obb旋转框检测的onnx模型

【官方框架地址】 https://github.com/ultralytics/ultralytics 【算法介绍】 Yolov11-obb&#xff08;You Only Look Once version 8 with Oriented Bounding Boxes&#xff09;是一种先进的对象检测算法&#xff0c;它在传统的Yolov3和Yolov4基础上进行了优化&#xff0c;加…
阅读更多...
Python 如何使用 scikit-learn 进行模型训练

Python 如何使用 scikit-learn 进行模型训练

如何使用 scikit-learn 进行模型训练 一、简介 在现代的数据科学和机器学习领域&#xff0c;Python 已经成为最流行的编程语言之一。而其中最流行的机器学习库之一就是 scikit-learn。scikit-learn 提供了许多方便的工具和函数来实现常见的机器学习任务&#xff0c;包括数据预…
阅读更多...
spi hal库 正点原子版

spi hal库 正点原子版

这个图 是了解一下 spi就是cs片选&#xff0c;clk时钟&#xff0c;miso主机输入从机输出&#xff0c;mosi主机输出从机输入&#xff0c;这四根线 spi最主要就是极性和相位的选择&#xff0c;spi是边沿采集&#xff0c;和iic的电平采集不一样&#xff0c;所以需要通过极性和相位…
阅读更多...
SpringBoot 多元化配置（正则表达式，配置文件优先级）

SpringBoot 多元化配置（正则表达式，配置文件优先级）

1.配置绑定 所谓“配置绑定”就是把配置文件中的值与 JavaBean 中对应的属性进行绑定。通常&#xff0c;我们会把一些配置信息&#xff08;例如&#xff0c;数据库配置&#xff09;放在配置文件中&#xff0c;然后通过 Java 代码去读取该配置文件&#xff0c;并且把配置文件中…
阅读更多...
【持续更新中】MMDetection3训练自己的数据集常见报错解决

【持续更新中】MMDetection3训练自己的数据集常见报错解决

博主近来跑自己数据集需要对比试验&#xff0c;故选择了MMDetection3这一算法整合详细的框架&#xff0c;遇到了较多问题在此处留作记录&#xff0c;若你也有相应的问题可以在评论区提出与解决方法。会持续更新&#xff0c;同时欢迎批评指正。 0.ModuleNotFoundError: No modu…
阅读更多...
从博士到院士，国家级人才荣誉称号一览

从博士到院士，国家级人才荣誉称号一览

在中国的科技界&#xff0c;两院院士代表着学术成就的巅峰荣誉&#xff0c;享有终身荣耀&#xff0c;并且是科研人员梦寐以求的最高职业荣誉。除了院士头衔之外&#xff0c;国家和各部委还设立了一系列针对不同年龄段学术人才的国家级荣誉称号体系&#xff0c;旨在表彰各类优秀…
阅读更多...
8.9K Star，开源自托管离线翻译引擎

8.9K Star，开源自托管离线翻译引擎

Hi&#xff0c;骚年&#xff0c;我是大 G&#xff0c;公众号「GitHub 指北」会推荐 GitHub 上有趣有用的项目&#xff0c;一分钟 get 一个优秀的开源项目&#xff0c;挖掘开源的价值&#xff0c;欢迎关注。 在全球化的今天&#xff0c;跨语言交流已成为日常需求&#xff0c;然…
阅读更多...
U3D游戏开发之中剧情系统的制作

U3D游戏开发之中剧情系统的制作

今天我们来揭秘带有人物选项的剧情系统该如何制作。 半年前我接到了一个剧情系统的需求&#xff0c;本着能抄代码绝不自己动手的想法在B站上面找现成系统&#xff0c;大概看了一些内容&#xff0c;发现比较繁琐就直接自己动手写了。 目录 1 需求分析 2 梳理代码逻辑 3 代码书…
阅读更多...
k8s 中存储之 NFS 卷

k8s 中存储之 NFS 卷

目录 1 NFS 卷的介绍 2 NFS 卷的实践操作 2.1 部署一台 NFS 共享主机 2.2 在所有k8s节点中安装nfs-utils 2.3 部署nfs卷 2.3.1 生成 pod 清单文件 2.3.2 修改 pod 清单文件增加 实现 NFS卷 挂载的 参数 2.3.3 声明签单文件并查看是否创建成功 2.3.4 在 NFS 服务器 创建默认发布…
阅读更多...
[c语言]一句话讲清循环中break和continue的作用与区别

[c语言]一句话讲清循环中break和continue的作用与区别

1.两者的作用 break和contuinue都只能在循环中使用&#xff0c;都用来停止循环。 2.两者的区别 break 在循环中只要遇到break&#xff0c;就直接永久终止当前循环&#xff0c;开始执行当前循环之外的代码。 continue 在循环中只要遇到continue&#xff0c;就结束本次循环&…
阅读更多...
免费送源码：Java+ssm+JSP+Ajax SSM棕榈校园论坛的开发 计算机毕业设计原创定制

免费送源码：Java+ssm+JSP+Ajax SSM棕榈校园论坛的开发 计算机毕业设计原创定制

摘要 随着计算机科学技术的高速发展,计算机成了人们日常生活的必需品&#xff0c;从而也带动了一系列与此相关产业&#xff0c;是人们的生活发生了翻天覆地的变化&#xff0c;而网络化的出现也在改变着人们传统的生活方式&#xff0c;包括工作&#xff0c;学习&#xff0c;社交…
阅读更多...
数据库软题6.1-关系模式-关系模式的各种键

数据库软题6.1-关系模式-关系模式的各种键

关系模式的各种键 题1-由关系模式求候选键 1. 候选键唯一不冗余 对选项进行闭包运算&#xff0c;如果得到全部属性U&#xff0c;则为候选码 A:AC-ABC-ABCD B:AB-ABC-ABCD C:AE-ABE-ABCE -ABCDE-ABCDEH D:DE2. R的候选码可以从A1,A2,A3,A1A2,A1A3,A2A3,A1A2A3中选择&#xff…
阅读更多...
Flutter String 按 ，。分割

Flutter String 按 ，。分割

在 Flutter 中&#xff0c;如果你想将一个字符串按特定的字符&#xff08;例如中文逗号 &#xff0c; 和英文句号 .&#xff09;进行分割&#xff0c;可以使用 Dart 语言的字符串处理功能。具体来说&#xff0c;你可以使用 split 方法&#xff0c;并传入一个正则表达式来匹配这…
阅读更多...
CSS基础-常见属性（二）

CSS基础-常见属性（二）

6、CSS三大特性 6.1 层叠性 如果样式发生冲突&#xff0c;则按照优先级进行覆盖。 6.2 继承性 元素自动继承其父元素、祖先元素所设置的某些元素&#xff0c;优先继承较近的元素。 6.3 优先级 6.3.1 简单分级 1、内联样式2、ID选择器3、类选择器/属性选择器4、标签名选择器/…
阅读更多...
数据结构之树（1）

数据结构之树（1）

课程&#xff1a;b站王道数据结构 5.1.1 树的定义和基本术语_哔哩哔哩_bilibili 写在前面&#xff1a;基础不牢&#xff0c;地动山摇。。 一、树 1、概念 树是n&#xff08;n>0)个结点的有限集合&#xff0c;n0时&#xff0c;称为空树 非空树的特性 有且仅有一个根节点…
阅读更多...
智能家居有哪些产品？生活中常见的人工智能有哪些？

智能家居有哪些产品？生活中常见的人工智能有哪些？

智能家居有哪些产品? 1、智能照明设备类&#xff1a;智能开关、智能插座、灯控模块、智能空开、智能灯、无线开关。 2、家庭安防类&#xff1a;智能门锁、智能摄像机、智能猫眼、智能门铃。 3、智能传感器类&#xff1a;烟雾传感器、可燃气体传感器、水浸传感器、声光报警器…
阅读更多...
CentOS7系统配置Yum环境

CentOS7系统配置Yum环境

新安装完系统的服务器往往缺少我们常用的依赖包&#xff0c;故需要设置好yum源&#xff0c;方便软件安装&#xff0c;以下是CentOS7为例&#xff0c;系统安装后yum默认安装。 //备份之前的配置文件 mv /etc/yum.repos.d /etc/yum.repos.d.bak mkdir -p /etc/yum.repos.d 1…
阅读更多...
鸿蒙开发之ArkUI 界面篇 十八 京东app登录界面实现

鸿蒙开发之ArkUI 界面篇 十八 京东app登录界面实现

鸿蒙UI实现某东App登录界面，如下图鲜果，我们先分析整体架构是什么！ 我们整体架构分析，分为区域1、2、3、4、5、6、7、8、9区域，下图： 8个区域的整体方向是垂直的，容器使用的是Column，区域1使用的是子容器Row，左边是Image，右边是Text，区域2是Image，区域3第一感觉是…
阅读更多...
欧姆龙(Omron)协议解析

欧姆龙(Omron)协议解析

1. 协议概述    欧姆龙(Omron)是来自日本的知名电子和自控设备制造商&#xff0c;其中、小型PLC在国内市场有较高的占有率&#xff0c;有CJ、CM等系列。PLC可以支持Fins、Host link等协议进行通信。 支持以太网的欧姆龙PLC CPU、以太网通信模块根据型号的不同&#xff0c;一般…
阅读更多...
dockertop提示Failed to fetch extensions

dockertop提示Failed to fetch extensions

解决办法&#xff1a;重装dockertop 第一步&#xff1a;卸载当前的dockertop 如果卸载过程中存在AlibabaProtect的相关软件关不掉&#xff0c;那么参考这篇文章&#xff1a;卸载AlibabaProtect 第二步&#xff1a;删除C:\Program Files路径下的Docker文件夹 第三步&#xff1…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023