为什么return 非常重要

在选择哪个策略更好的时候，此时需要使用到return，比如下面三个策略的返回值。

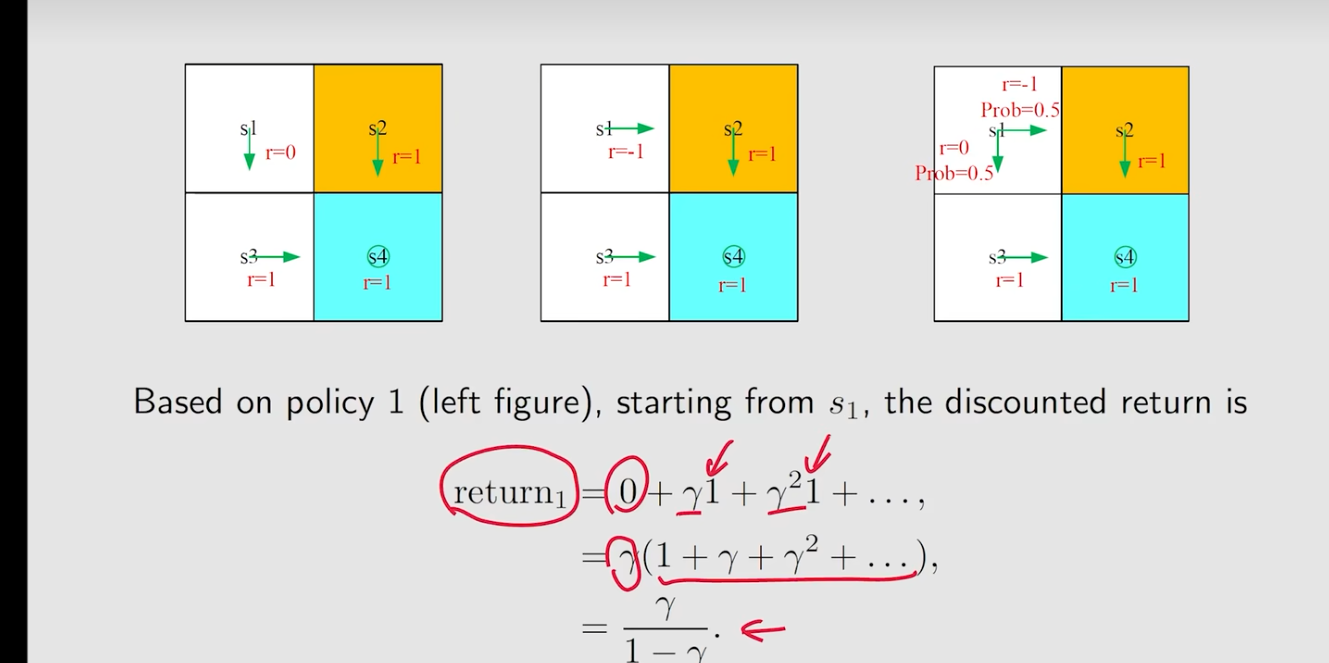
• 策略1:
• 策略2：
• 策略3：涉及到两个policy's path

  

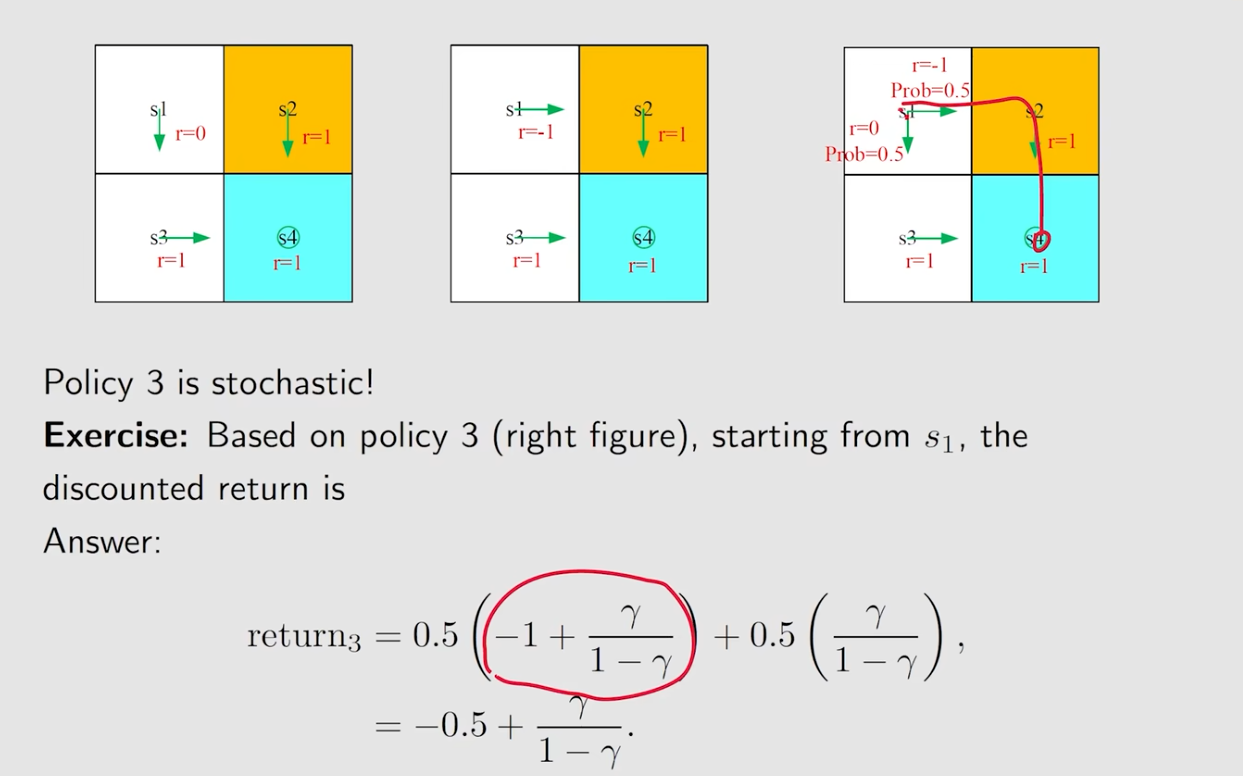
How to calculate return

• 定义

上图定义了不同的起点下的return value

• 递推式

The returns rely on the others' return. - >Bootstrapping.

• 矩阵化

可以写成矩阵的形式 -> 贝尔曼公式：

state value

• 单步的过程

• 多步的过程

• state value 是关于s（状态）的function，不同的状态会得到不同的state value
• state value是基于policy的，不同的policy得到不同的state value
• 如果state value greater，那么这个策略会更好，因为更多的分数可以得到

贝尔曼公式

• 

• • calculate 

• • • 

      其实就是对当前的状态s的情况下求不同的action在策略概率下在下一个时刻得分的平均代表我在当前状态s，经过action a得到分数r的概率。表示当前状态是s，执行action a的概率。

• • • 

• • • • 这里有几个注意点，首先无记忆性，就是当我已经知道了那么就不需要知道
      • 表示，当前的状态是s，采取行动a，到达状态s'的期望

贝尔曼公式

• 描述了state-value 在不同的state的关系
• 两种不同的term 瞬时回报（immediate reward） 和future reward
• 这不是一个式子，是一个状态的集合式子，比如n个状态，n个式子

  

• v_π(s) 和 v_π(s') 是我们要计算的状态值，计算的思想就是 Bootstrapping ! 直观上来讲，等式左边的状态值（state value）v_π(s) 依赖于等式右边的状态值（state value）v_π(s') ，看起来好像没法计算，其实我们有一组这样的式子，把这些式子连立就可以算出来。
• 公式中的 π(a|s) 是给定的策略 policy（是一种概率 probability）。解方程称为策略评估（policy evaluation）：贝尔曼公式依赖于策略（policy），如果我们能计算出状态值（state value），其实我们在做的一件事就是评估这个策略（policy evaluation）究竟是好是坏。
• 奖励概率 （Reward probability） p(r|s,a) 和状态转换概率（State transition probability） p(s'|s,a) 代表的是动态模型（dynamic model）或称为环境模型（environment model）：分两种情况，一种是我们知道这个模型（model），在本节和下节当中我们都会假设知道这个 model，给出来相应的算法；一种是不知道模型（model），这种情况下我们仍然可以求出 state value，这就是 model free reinforcement learning 的算法。

例子

当在S1状态的时候求贝尔曼公式：

• 因为只有一个action的概率，所以其它为0，可以把求和拿掉
• 乘起来为0，因为其它的r的得分概率为0，那么这一项为0，不需要求和

得出：

这里得到s1的state value的值为8.5，这个policy是没有上一个policy好的

Matrix-vector form

• 将公式简化

• 向量化

这里的v，r向量化都很明显，这里的P，实际上是利用举证的乘法，对于其中的是一个列向量，那么就是每一行的值和其列向量相乘得到不同的i对应不同的j的和

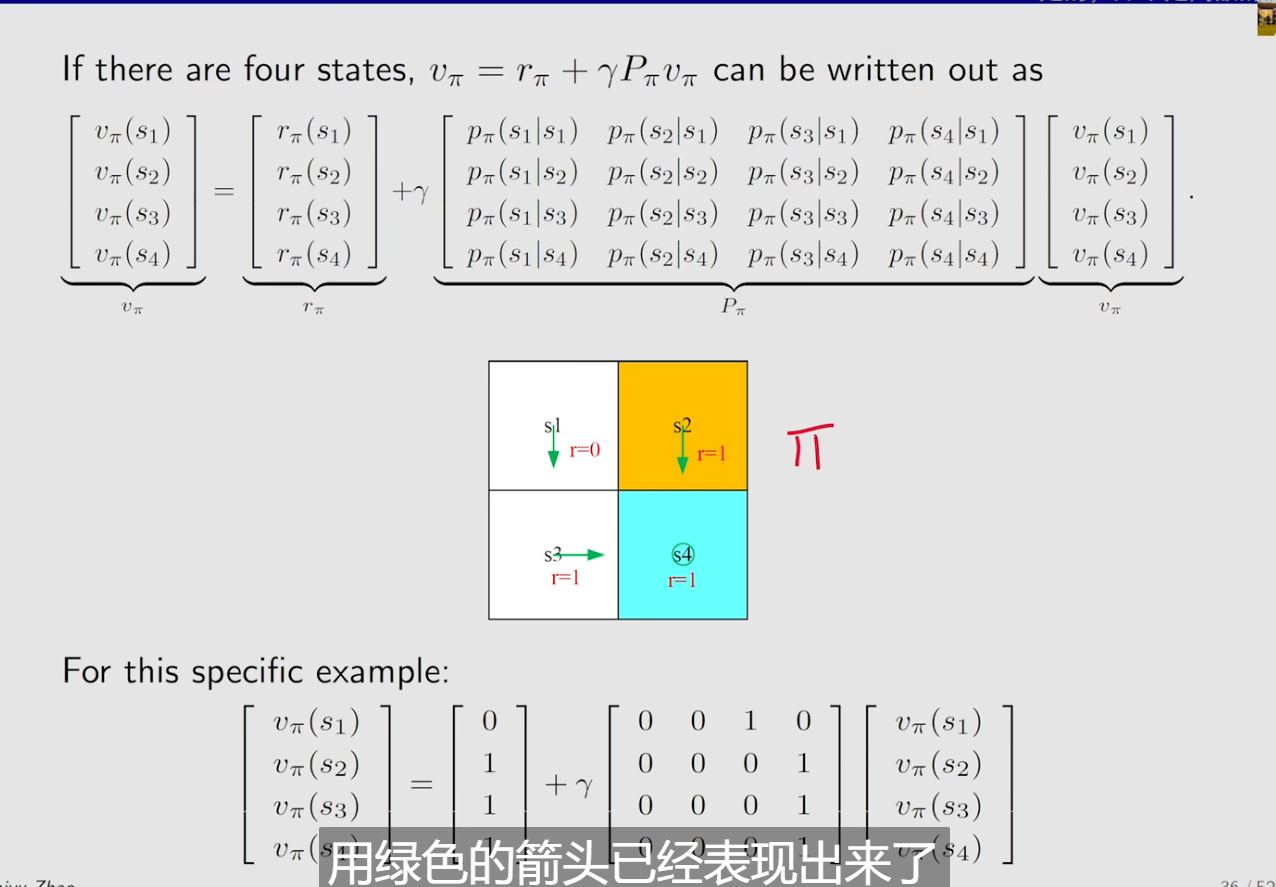
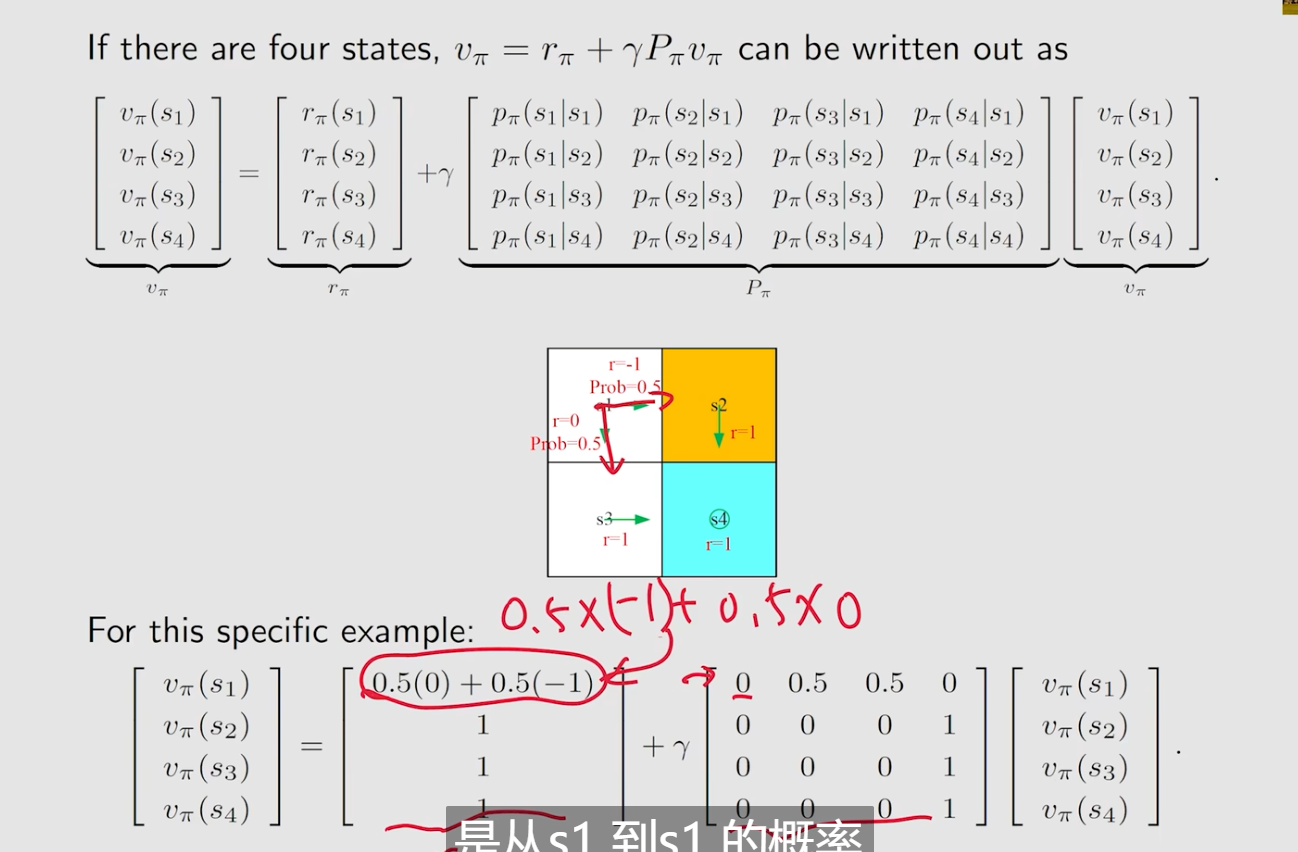
得到state value是因为我们需要去评价这个policy

• 近似法

可以证明当趋向无穷的时候，这个收敛于。以下是证明：

例子

以下考虑比较好的两个策略

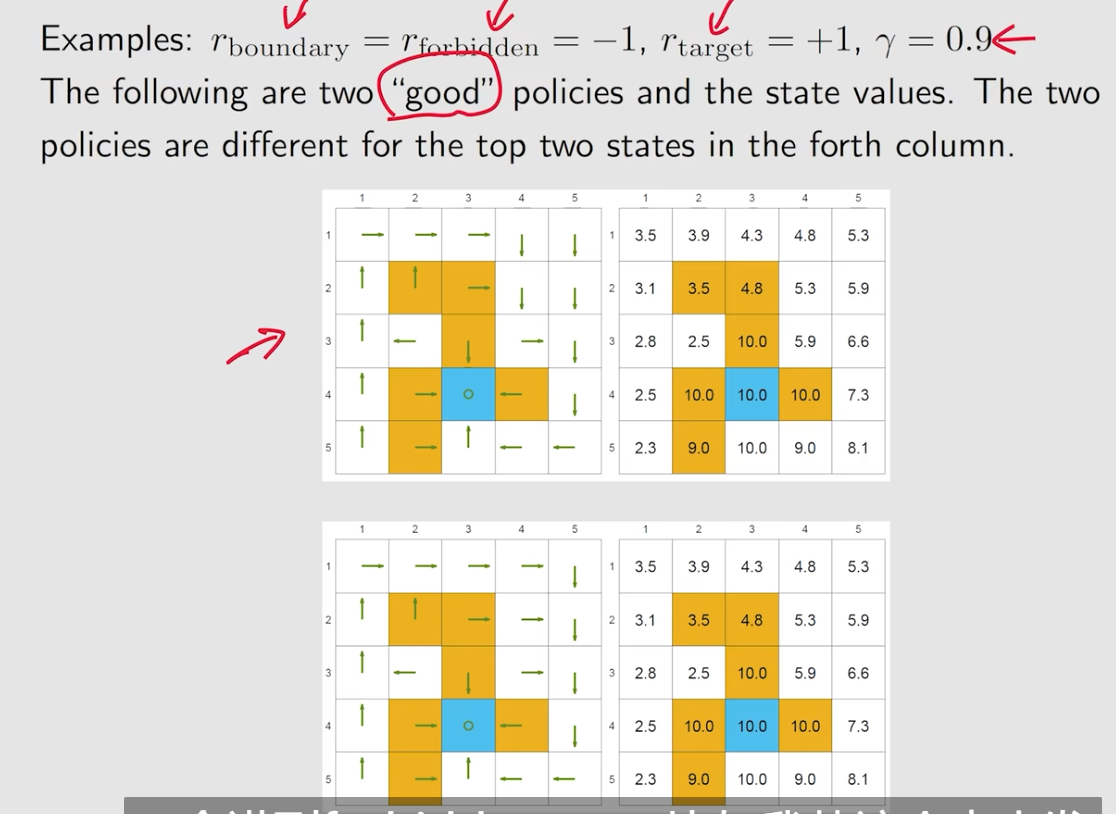
• 靠近target的state value都会比较大，越远越小

比较差的策略

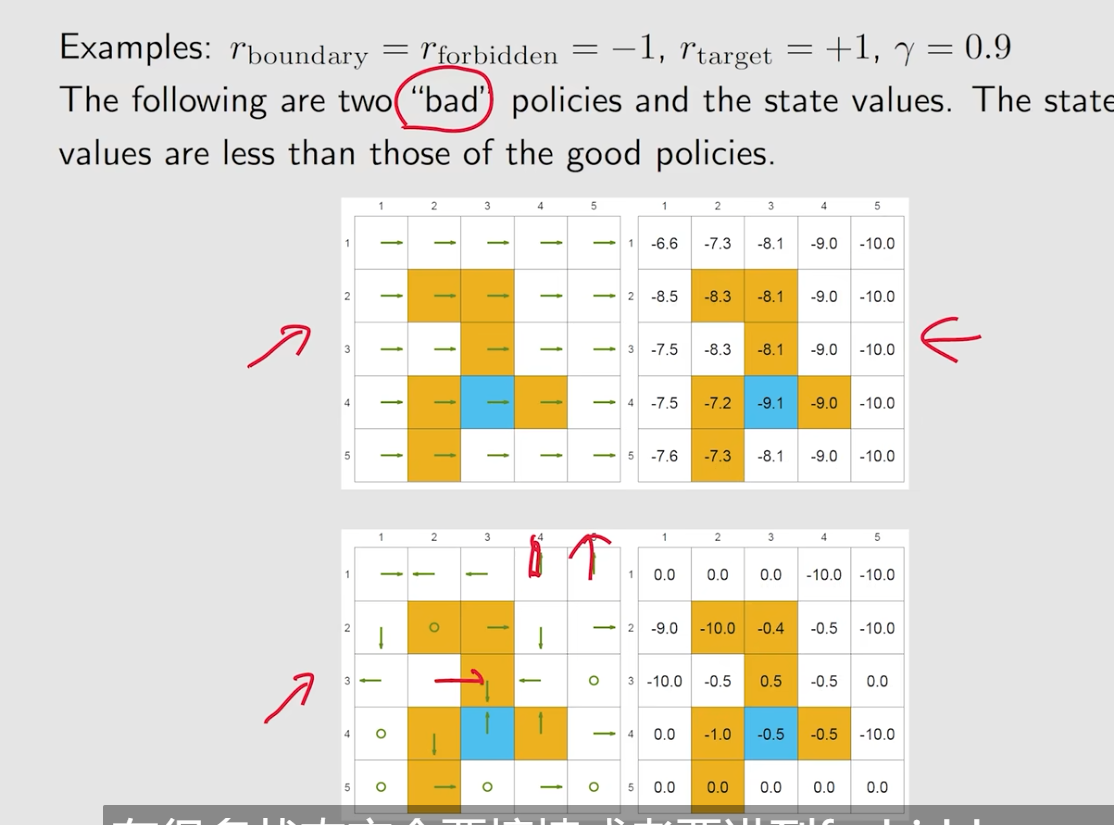
action value

• action value

从一个状态和action出发得到的average return。当我们需要知道哪个action更加好时，使用action value

action value definition

• 
• 它是一个state-action函数
• 它依赖于策略Π

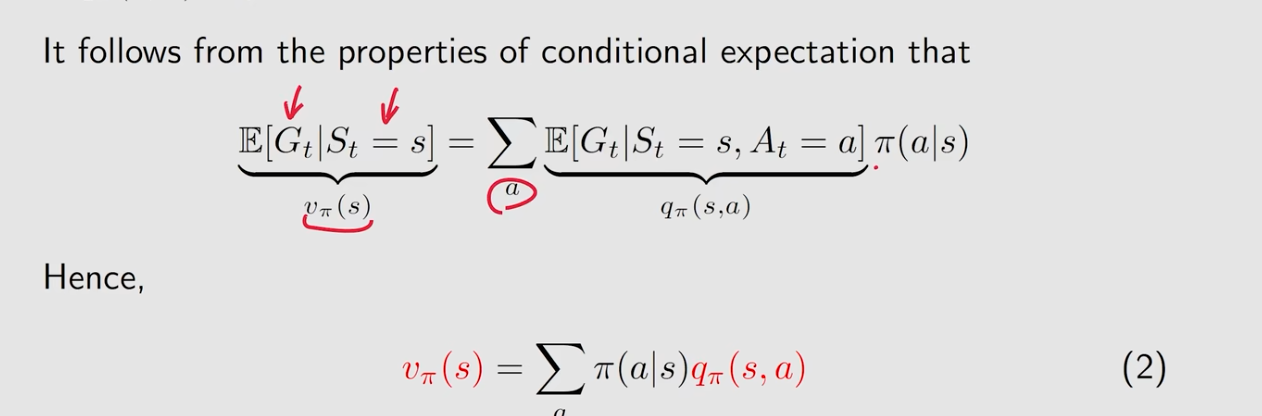
action value和state value的关系

=>

• 知道state value可以求得action value
• 知道action value可以求得state value

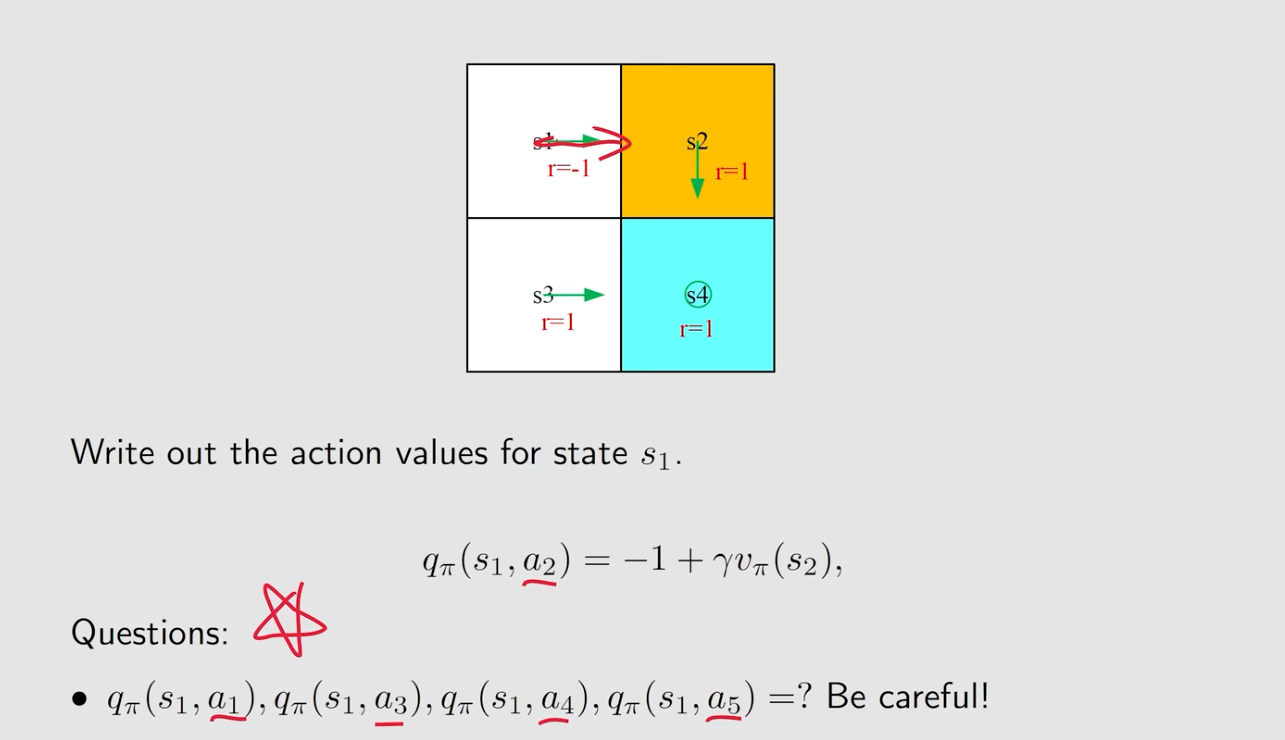
• 虽然这个策略只告诉我们a2，但是实际上每一个action的action value都需要计算

• 比如，撞墙为-1分，因为撞墙还是可以回来