二项分布（Binomial Distribution） 是概率论和统计学中描述独立重复的伯努利试验中成功次数的离散概率分布。它是基于多次独立的伯努利试验的扩展，用于描述在 $n$ 次试验中发生成功的次数。

1. 二项分布的定义

二项分布用于描述在 $n$ 次独立的伯努利试验中，成功发生的次数。每次伯努利试验只有两种结果——成功或失败，成功的概率为 $p$，失败的概率为 $1-p$。

概率质量函数（PMF）

如果随机变量 $X$ 表示 $n$ 次独立的伯努利试验中成功的次数，且成功的概率为 $p$，那么 $X$ 服从二项分布，记为：

$$X\sim \text{Bin}(n,p)$$

二项分布的概率质量函数（PMF）为：

$$P(X=k)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)p^k(1-p{)}^{n-k}$$

其中：

• $X$ 是成功的次数。
• $n$ 是试验次数（即进行的独立伯努利试验的总次数）。
• $p$ 是每次试验成功的概率。
• $\left(\genfrac{}{}{0ex}{}{n}{k}\right)$ 是组合数，表示从 $n$ 次试验中选择 $k$ 次成功的方式数，公式为：

$$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\frac{n!}{k!(n-k)!}$$

---

2. 二项分布的性质

a. 期望值（Expectation）

二项分布的期望值表示在 $n$ 次试验中成功的平均次数。二项分布的期望值 $E(X)$ 为：

$$E(X)=np$$

这意味着，成功的平均次数是试验次数 $n$ 和单次成功概率 $p$ 的乘积。例如，投掷硬币 10 次，如果每次正面的概率为 0.5，则出现正面的期望次数是 $10\times 0.5=5$。

b. 方差（Variance）

方差描述成功次数的波动性或离散程度。二项分布的方差 $Var(X)$ 为：

$$Var(X)=np(1-p)$$

方差表明，成功次数的波动性取决于试验次数 $n$、成功概率 $p$ 和失败概率 $1-p$。

c. 标准差（Standard Deviation）

标准差是方差的平方根，用于衡量成功次数的波动程度：

$$\sigma (X)=\sqrt{np(1-p)}$$

d. 二项分布的形状

• 当 $p=0.5$ 时，二项分布是对称的，成功和失败的概率相等。此时，分布的平均值位于 $n/2$ 附近。
• 当 $p>0.5$ 时，分布向右偏斜，成功的次数更可能接近 $n$。
• 当 $p<0.5$ 时，分布向左偏斜，成功的次数更可能接近 0。

图例说明如下：

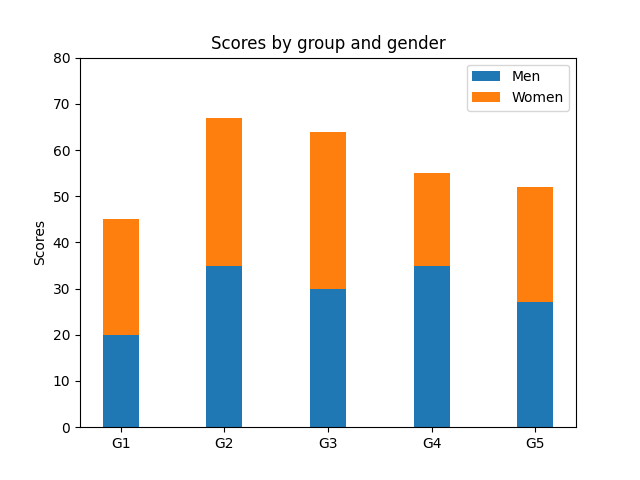
这张图展示了三种不同参数设置下的二项分布，其中横坐标表示随机变量（成功次数），纵坐标表示每个随机变量对应的概率（即发生特定成功次数的概率）。

图片来源：https://medium.com/@abhishekjainindore24/all-about-binomial-distribution-ba476ea4642f

图中展示了三个不同的二项分布：

1. 绿色柱形图：$p=0.5$ 且 $n=20$，表示进行了 20 次试验，每次成功的概率为 0.5。分布呈对称形状，均值大约在 10 次成功附近（$n\times p=20\times 0.5=10$）。

2. 棕色柱形图：$p=0.7$ 且 $n=20$，表示进行了 20 次试验，每次成功的概率为 0.7。分布向右偏斜，表示成功次数更多，均值接近 14 次（$n\times p=20\times 0.7=14$）。

3. 紫色柱形图：$p=0.5$ 且 $n=40$，表示进行了 40 次试验，每次成功的概率为 0.5。分布较宽且更加集中，均值大约在 20 次成功附近（$n\times p=40\times 0.5=20$）。

总结：

• $n$（试验次数）：随着 $n$ 增大，分布变得更加集中和对称。
• $p$（成功概率）：随着 $p$ 增大，分布向右偏斜，成功次数的期望值增加。

---

3. 二项分布的例子

二项分布适用于任何重复的独立伯努利试验，即每次试验结果只可能是成功或失败，并且每次试验的成功概率 $p$ 是相同的。

例子1：投掷硬币

假设我们进行 10 次独立的投掷硬币实验，每次投掷硬币的正面朝上的概率为 $p=0.5$。令 $X$ 表示正面朝上的次数，则 $X\sim \text{Bin}(10,0.5)$。

计算恰好有 6 次正面朝上的概率：

$$P(X=6)=\left(\genfrac{}{}{0ex}{}{10}{6}\right)(0.5{)}^6(0.5{)}^4=\frac{10!}{6!4!}(0.5{)}^{10}=0.205$$

即，在 10 次投掷硬币中，有 6 次正面朝上的概率为 0.205。

例子2：考试通过率

假设某场考试的通过率为 80%，某班有 10 个学生参加考试。我们可以用二项分布来描述通过考试的学生人数。令 $X$ 表示通过考试的学生人数，则 $X\sim \text{Bin}(10,0.8)$。

计算恰好有 8 个学生通过考试的概率：

$$P(X=8)=\left(\genfrac{}{}{0ex}{}{10}{8}\right)(0.8{)}^8(0.2{)}^2=0.302$$

即，恰好有 8 个学生通过考试的概率为 0.302。

---

4. 二项分布的推导

二项分布是通过 $n$ 次独立的伯努利试验推导出来的，每次试验的结果是独立的成功或失败。

a. 组合数的解释

$\left(\genfrac{}{}{0ex}{}{n}{k}\right)$ 代表从 $n$ 次试验中选择 $k$ 次成功的方式数。组合数的公式为：

$$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\frac{n!}{k!(n-k)!}$$

它表示有多少种方式可以从 $n$ 次试验中选择 $k$ 次成功。

b. 成功和失败的概率

成功发生 $k$ 次的概率为 $p^k$，而失败发生 $n-k$ 次的概率为 $(1-p{)}^{n-k}$。二项分布的概率质量函数是这三部分的乘积：

$$P(X=k)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)p^k(1-p{)}^{n-k}$$

这就是二项分布的公式，表示在 $n$ 次试验中恰好有 $k$ 次成功的概率。

---

5. 二项分布与其他分布的关系

a. 伯努利分布

二项分布是伯努利分布的推广。伯努利分布表示单次伯努利试验的成功或失败，而二项分布表示多次独立的伯努利试验中的成功次数。

• 如果 $n=1$，则二项分布退化为伯努利分布。

b. 泊松分布

当 $n$ 很大而 $p$ 很小时，且 $n\cdot p=\lambda$ 是常数时，二项分布趋近于泊松分布。这种情况下，二项分布可以用来近似泊松分布，描述稀有事件的发生次数。

c. 正态分布

当试验次数 $n$ 很大时，二项分布可以近似为正态分布。这是因为根据中心极限定理，当 $n$ 较大时，二项分布的形状逐渐趋于对称，并且接近正态分布。

• 当 $np>5$ 且 $n(1-p)>5$ 时，二项分布可以用正态分布进行近似。

---

6. 二项分布的实际应用

a. 质量控制

在质量控制中，二项分布用于描述生产线中合格产品和不合格产品的数量。例如，从生产线上随机抽取 100 个产品，检查其中有多少个合格产品，这可以用二项分布来建模。

b. 市场营销

二项分布用于建模市场营销中的成功概率。例如，在发送电子邮件广告时，可以用二项分布来计算有多少人会响应广告。

c. 生物统计

在生物统计学中，二项分布用于建模二元结果（如存活/死亡、健康/疾病等）的实验。例如，进行 100 次药物实验，记录有多少病人康复。

---

7. 总结

二项分布 是描述多次独立伯努利试验中成功次数的离散概率分布。它通过组合数计算成功次数的方式数，并将成功和失败的概率组合在一起，得到在 $n$ 次试验中成功 $k$ 次的概率。二项分布广泛应用于统计学、质量控制、市场营销、医学实验等领域，用于建模多次重复试验中某个事件发生的次数。