二、openCV+TensorFlow入门

news2024/12/29 10:51:33

目录

  • 一、openCV入门
    • 1 - 简单图片操作
    • 2 - 像素操作
  • 二、TensorFlow入门
    • 1 - TensorFlow常量变量
    • 2 - TensorFlow运算本质
    • 3 - TensorFlow四则运算
    • 4 - tensorflow矩阵基础
    • 5 - numpy矩阵
    • 6 - matplotlib绘图
  • 三、神经网络逼近股票收盘均价（案例）
    • 1 - 绘制15天股票K线的柱状图
    • 2 - 人工神经网络简介
    • 3 - 编码实现

一、openCV入门

1 - 简单图片操作

  • 图片读取与展示：imread第2参数，0表示灰度图片，1表示彩色图片
import cv2 
# 1 文件的读取 2 封装格式解析 3 数据解码 4 数据加载
img = cv2.imread('image0.jpg',1)
cv2.imshow('image',img)
# jpg png  1 文件头 2 文件数据
cv2.waitKey (0)
# 1.14M 130k
  • 图片写入
import cv2
img = cv2.imread('image0.jpg',1)
cv2.imwrite('image1.jpg',img) # 1 name 2 data
  • 有损压缩：cv2.IMWRITE_JPEG_QUALITY，范围是0-100，数字越大图片越清晰
    • 可以看到压缩后为35kb，同时图片质量降低了
import cv2
img = cv2.imread('image0.jpg',1)
cv2.imwrite('imageTest.jpg',img,[cv2.IMWRITE_JPEG_QUALITY,50])
#1M 100k 10k 0-100 有损压缩

在这里插入图片描述
在这里插入图片描述

  • png压缩：cv2.IMWRITE_PNG_COMPRESSION，压缩范围0-9，数字越小图片越清晰
    • 特点1：png是无损压缩
    • 特点2：png有图像透明度，jpg是没有图像透明度属性的

2 - 像素操作

  • RGB：每一种颜色（像素）都是由RGB三种分量构成的
  • 颜色深度：对于8位的颜色深度来说，可以表示0-255；也就是说一个颜色可以使用256256256来表示
  • 图片的宽高：比如w：h = 640 * 480 -> 这个表示在水平方向上有640个像素点，在垂直方向上有480个像素点
  • 图片的大小计算：假设图片的宽为720，高位547；那么图片的大小=7205473*8 bit/8（B）=1.14M
    • 其中720是宽，547是高，3代表RGB三种分量，第1个8代表是8位，第2个8代表bit转成B
  • alpha通道：图片的透明度信息，上面介绍过png是无损压缩，有透明度信息
  • BGR：颜色深度格式，除了RGB之外，还有BGR
    • opencv读取图片时获取的是bgr
    • BGR与RGB不同的是第一个像素值是B蓝色
    • BGR每个称之为一个分量，每个分量又叫做颜色通道
  • 案例：像素读取与写入：注意像素写入的时候第一个是b
import cv2

# 像素的读取
img = cv2.imread('image0.jpg', 1)
(b, g, r) = img[100, 100]
print(b, g, r)  # bgr

# 像素的写入
for i in range(1, 100):
    img[10 + i, 100] = (255, 0, 0)
cv2.imshow('image', img)
cv2.waitKey(0)

在这里插入图片描述

二、TensorFlow入门

1 - TensorFlow常量变量

  • 变量的使用注意：session使用前需要sess.run(init)初始化
import tensorflow as tf

data1 = tf.constant(2, dtype=tf.int32)
data2 = tf.Variable(10, name='var')
print(data1)
print(data2)

init = tf.global_variables_initializer()
sess = tf.Session()
with sess:
    sess.run(init)
    print(sess.run(data1))
    print(sess.run(data2))

在这里插入图片描述

2 - TensorFlow运算本质

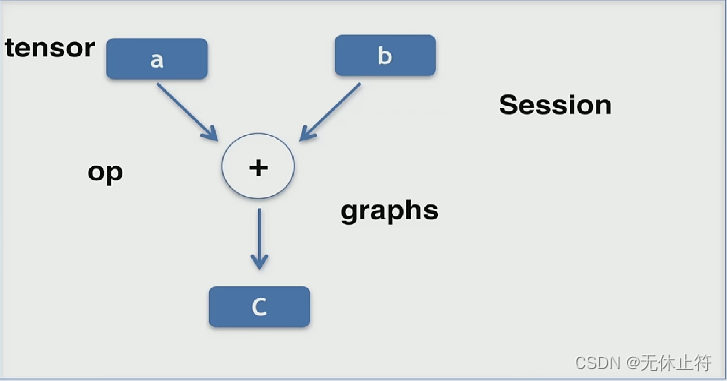
  • tensorflow的本质：张量tensor+计算图grahps
    • tf = tensor + grahps
    • tensor：数据
    • op：操作，可以是赋值操作也可以是四则运算操作
    • grahps：数据操作的过程
    • Session：在tf中所有的grahps都需要放到Session会话中来执行，Session可以理解成一个运算的交互环境
      在这里插入图片描述

3 - TensorFlow四则运算

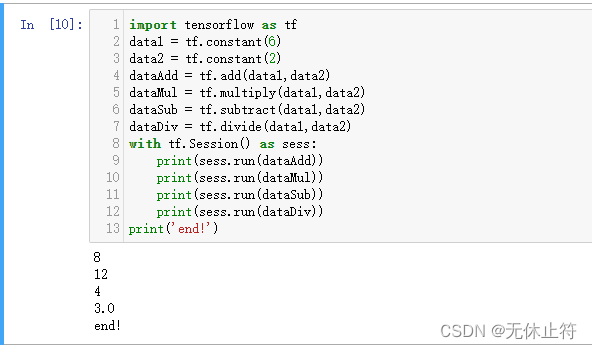
  • 常量间的四则运算
import tensorflow as tf
data1 = tf.constant(6)
data2 = tf.constant(2)
dataAdd = tf.add(data1,data2)
dataMul = tf.multiply(data1,data2)
dataSub = tf.subtract(data1,data2)
dataDiv = tf.divide(data1,data2)
with tf.Session() as sess:
    print(sess.run(dataAdd))
    print(sess.run(dataMul))
    print(sess.run(dataSub))
    print(sess.run(dataDiv))
print('end!')

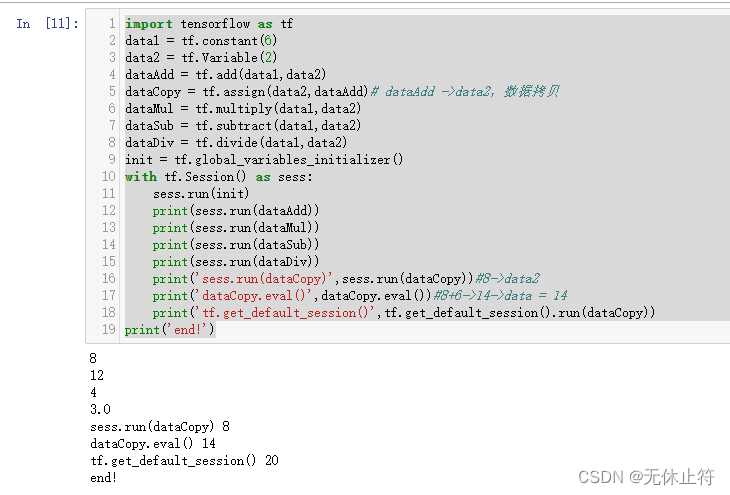
在这里插入图片描述

  • 常量变量间的四则运算
import tensorflow as tf

data1 = tf.constant(6)
data2 = tf.Variable(2)
dataAdd = tf.add(data1, data2)
dataCopy = tf.assign(data2, dataAdd)  # dataAdd ->data2，数据拷贝
dataMul = tf.multiply(data1, data2)
dataSub = tf.subtract(data1, data2)
dataDiv = tf.divide(data1, data2)
init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    print(sess.run(dataAdd))
    print(sess.run(dataMul))
    print(sess.run(dataSub))
    print(sess.run(dataDiv))
    print('sess.run(dataCopy)', sess.run(dataCopy))  # 8->data2
    print('dataCopy.eval()', dataCopy.eval())  # 8+6->14->data = 14
    print('tf.get_default_session()', tf.get_default_session().run(dataCopy))
print('end!')

在这里插入图片描述

4 - tensorflow矩阵基础

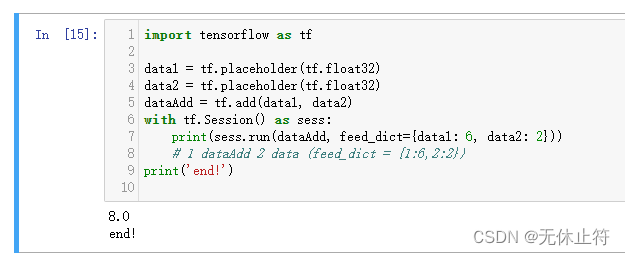
  • placeholder使用
import tensorflow as tf

data1 = tf.placeholder(tf.float32)
data2 = tf.placeholder(tf.float32)
dataAdd = tf.add(data1, data2)
with tf.Session() as sess:
    print(sess.run(dataAdd, feed_dict={data1: 6, data2: 2}))
    # 1 dataAdd 2 data (feed_dict = {1:6,2:2})
print('end!')

在这里插入图片描述

  • 矩阵加法：2个矩阵的行列要相同
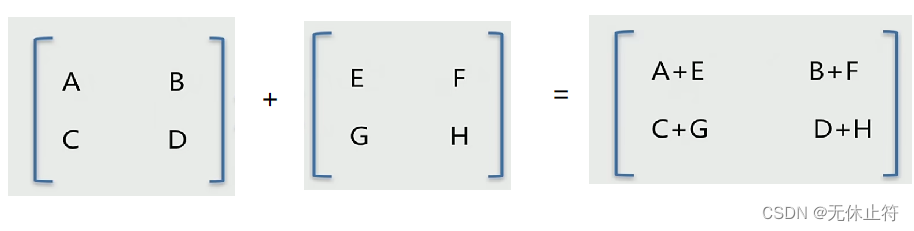
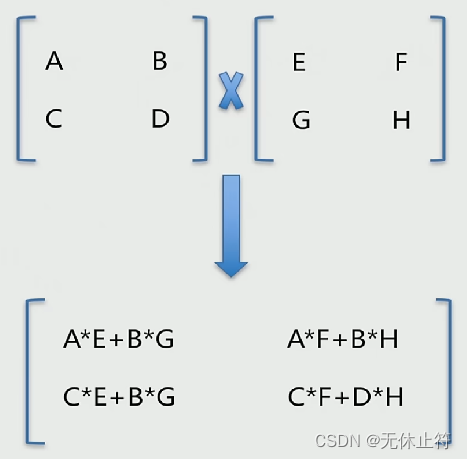
    在这里插入图片描述

  • 矩阵乘法：第1个矩阵的列数要和第2个矩阵的行数相同
    在这里插入图片描述

    • matmul：矩阵乘法，需要满足第1个矩阵的列数和第2个矩阵的行数相同
    • multiply：普通的乘法，无要求，两个矩阵对应元素相乘
import tensorflow as tf

data1 = tf.constant([[6, 6]])
data2 = tf.constant([[2],
                     [2]])
data3 = tf.constant([[3, 3]])
matMul = tf.matmul(data1, data2)
matMul2 = tf.multiply(data1, data2)
matAdd = tf.add(data1, data3)
with tf.Session() as sess:
    print(sess.run(matMul))  # 1 维 M=1 N=2. 1X2(MK) 2X1(KN) = 1(MN)
    print(sess.run(matAdd))  # 1行2列
    print(sess.run(matMul2))  # 1x2 2x1 = 2x2
    print(sess.run([matMul, matAdd]))  # 一次打印多个

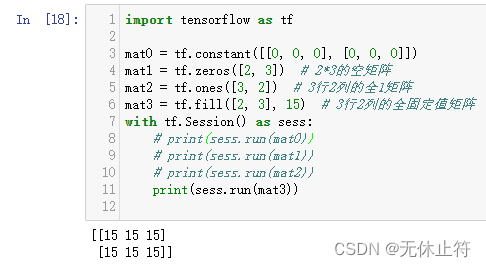
在这里插入图片描述

  • 矩阵填充：tf.zeros、tf.ones、tf.fill
import tensorflow as tf

mat0 = tf.constant([[0, 0, 0], [0, 0, 0]])
mat1 = tf.zeros([2, 3])  # 2*3的空矩阵
mat2 = tf.ones([3, 2])  # 3行2列的全1矩阵
mat3 = tf.fill([2, 3], 15)  # 3行2列的全固定值矩阵
with tf.Session() as sess:
    # print(sess.run(mat0))
    # print(sess.run(mat1))
    # print(sess.run(mat2))
    print(sess.run(mat3))

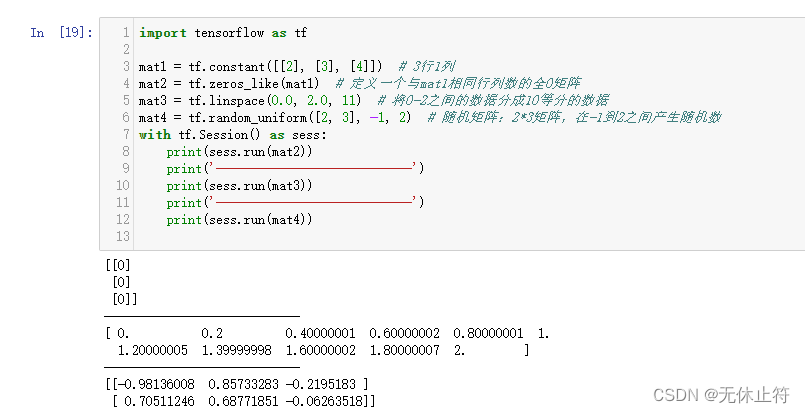
在这里插入图片描述

  • 其他矩阵操作
    • tf.zeros_like：填充维度相同的0矩阵
    • tf.linspace：生成等分数据的数组
    • tf.random_uniform：随机矩阵
import tensorflow as tf

mat1 = tf.constant([[2], [3], [4]])  # 3行1列
mat2 = tf.zeros_like(mat1)  # 定义一个与mat1相同行列数的全0矩阵
mat3 = tf.linspace(0.0, 2.0, 11)  # 将0-2之间的数据分成10等分的数据
mat4 = tf.random_uniform([2, 3], -1, 2)  # 随机矩阵：2*3矩阵，在-1到2之间产生随机数
with tf.Session() as sess:
    print(sess.run(mat2))
    print('----------------------------')
    print(sess.run(mat3))
    print('----------------------------')
    print(sess.run(mat4))

在这里插入图片描述

5 - numpy矩阵

import numpy as np

data1 = np.array([1, 2, 3, 4, 5])
print(data1)
data2 = np.array([[1, 2],
                  [3, 4]])
print(data2)
# 维度
print(data1.shape, data2.shape)
print('------------------------------')
# zero ones
print(np.zeros([2, 3]), '\n', np.ones([2, 2]))
# 改查
data2[1, 0] = 5
print(data2)
print(data2[1, 1])
print('------------------------------')
# 基本运算
data3 = np.ones([2, 3])
print(data3 * 2)  # 每个元素对应相乘
print(data3 / 3)
print(data3 + 2)
print('------------------------------')
# 矩阵+*
data4 = np.array([[1, 2, 3], [4, 5, 6]])
print(data3 + data4)  # 对应元素相加
print(data3 * data4)  # 对应元素相乘

在这里插入图片描述

6 - matplotlib绘图

  • 可以直接在anaconda中安装matplotlib
    在这里插入图片描述
  • matplotlib绘图
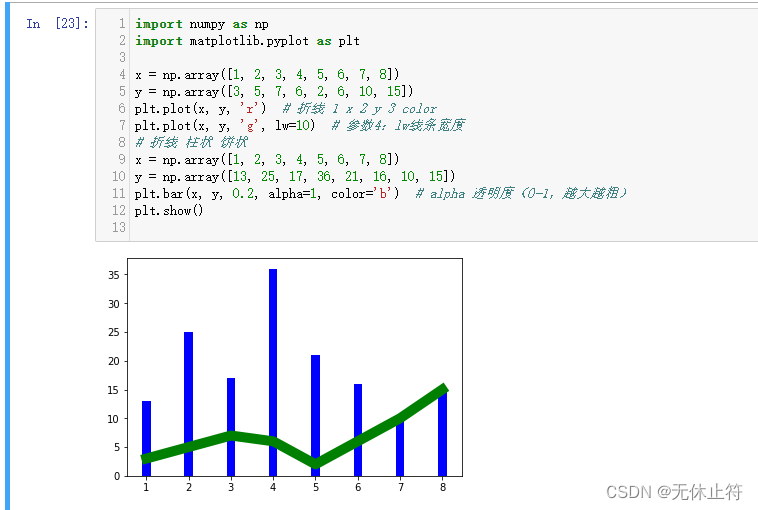
    • plt.plot：绘制折线图
    • plt.bar：绘制柱状图
import numpy as np
import matplotlib.pyplot as plt

x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
y = np.array([3, 5, 7, 6, 2, 6, 10, 15])
plt.plot(x, y, 'r')  # 折线 1 x 2 y 3 color
plt.plot(x, y, 'g', lw=10)  # 参数4：lw线条宽度
# 折线 柱状 饼状
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
y = np.array([13, 25, 17, 36, 21, 16, 10, 15])
plt.bar(x, y, 0.2, alpha=1, color='b')  # alpha 透明度（0-1，越大越粗）
plt.show()

在这里插入图片描述

三、神经网络逼近股票收盘均价（案例）

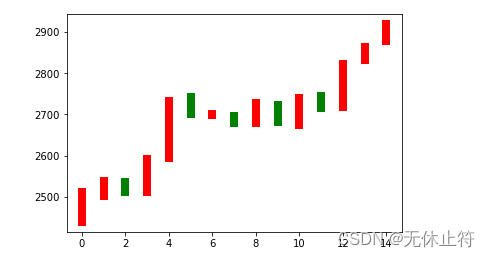
1 - 绘制15天股票K线的柱状图

import numpy as np
import matplotlib.pyplot as plt

date = np.linspace(1, 15, 15)  # 表示日期
# endPrice收盘价
endPrice = np.array(
    [2511.90, 2538.26, 2510.68, 2591.66, 2732.98, 2701.69, 2701.29, 2678.67, 2726.50, 2681.50, 2739.17, 2715.07,
     2823.58, 2864.90, 2919.08])
# beginPrice开盘价
beginPrice = np.array(
    [2438.71, 2500.88, 2534.95, 2512.52, 2594.04, 2743.26, 2697.47, 2695.24, 2678.23, 2722.13, 2674.93, 2744.13,
     2717.46, 2832.73, 2877.40])
print(date)
plt.figure()  # 绘图
for i in range(0, 15):
    dateOne = np.zeros([2])
    dateOne[0] = i
    dateOne[1] = i
    priceOne = np.zeros([2])
    priceOne[0] = beginPrice[i]
    priceOne[1] = endPrice[i]
    if endPrice[i] > beginPrice[i]:
        plt.plot(dateOne, priceOne, 'r', lw=8)  # 上涨
    else:
        plt.plot(dateOne, priceOne, 'g', lw=8)  # 下跌
plt.show()

在这里插入图片描述

2 - 人工神经网络简介

  • 人工神经网络三层：输入层、隐藏层（中间层）、输出层

在这里插入图片描述

  • 神经网络三层的转换公式
    • A代表输入矩阵、B代表隐藏矩阵、C代表输出矩阵
    • w代表权重矩阵
    • b代表偏置矩阵
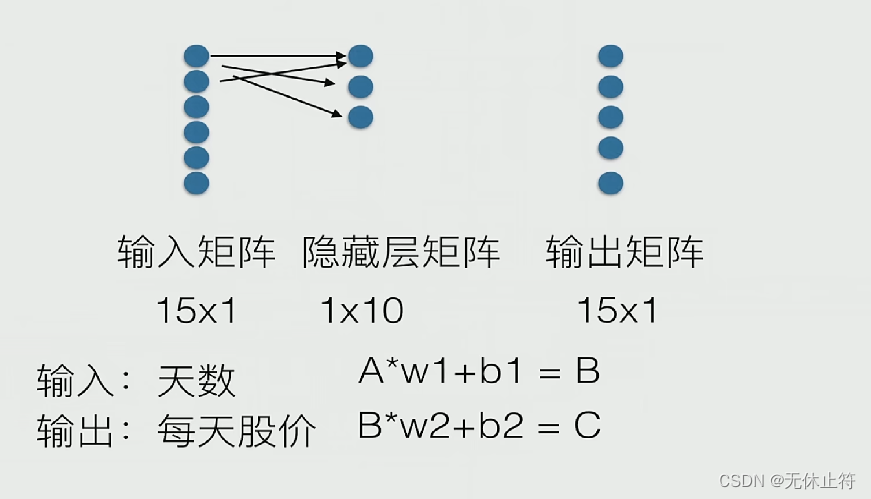
      在这里插入图片描述
  • 矩阵维度分析
    在这里插入图片描述
  • 梯度下降法：获取最终的w1w2b1b2
    • 终止的2种条件：根据循环次数控制；根据与真实的差异百分比控制
      在这里插入图片描述

3 - 编码实现

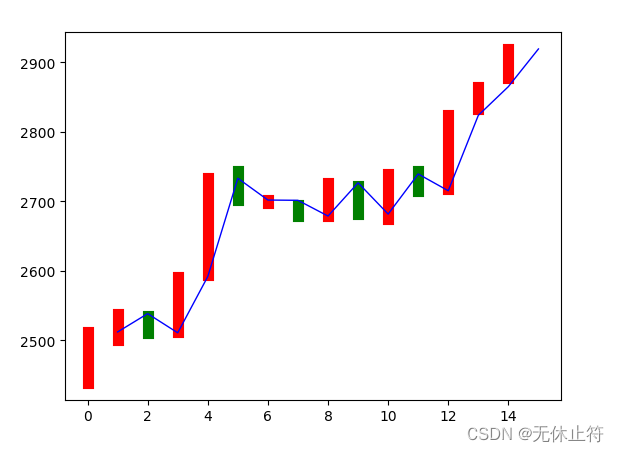
  • 结果说明：可以看到蓝色的折线图是预测的收盘价格，与实际的收盘价格还是比较接近的
# layer1：激励函数+乘加运算
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

date = np.linspace(1, 15, 15)
endPrice = np.array(
    [2511.90, 2538.26, 2510.68, 2591.66, 2732.98, 2701.69, 2701.29, 2678.67, 2726.50, 2681.50, 2739.17, 2715.07,
     2823.58, 2864.90, 2919.08]
)
beginPrice = np.array(
    [2438.71, 2500.88, 2534.95, 2512.52, 2594.04, 2743.26, 2697.47, 2695.24, 2678.23, 2722.13, 2674.93, 2744.13,
     2717.46, 2832.73, 2877.40])
print(date)
plt.figure()
for i in range(0, 15):
    # 1 柱状图
    dateOne = np.zeros([2])
    dateOne[0] = i
    dateOne[1] = i
    priceOne = np.zeros([2])
    priceOne[0] = beginPrice[i]
    priceOne[1] = endPrice[i]
    if endPrice[i] > beginPrice[i]:
        plt.plot(dateOne, priceOne, 'r', lw=8)
    else:
        plt.plot(dateOne, priceOne, 'g', lw=8)
# plt.show()
# A(15x1)*w1(1x10)+b1(1*10) = B(15x10)
# B(15x10)*w2(10x1)+b2(15x1) = C(15x1)
# 1 A B C
# 归一化
dateNormal = np.zeros([15, 1])
priceNormal = np.zeros([15, 1])
for i in range(0, 15):
    dateNormal[i, 0] = i / 14.0
    priceNormal[i, 0] = endPrice[i] / 3000.0

# 数据装载
x = tf.placeholder(tf.float32, [None, 1])  # N行1列
y = tf.placeholder(tf.float32, [None, 1])
# 隐藏层
w1 = tf.Variable(tf.random_uniform([1, 10], 0, 1))
b1 = tf.Variable(tf.zeros([1, 10]))
wb1 = tf.matmul(x, w1) + b1
layer1 = tf.nn.relu(wb1)  # 激励函数：简单的映射
# 输出层
w2 = tf.Variable(tf.random_uniform([10, 1], 0, 1))
b2 = tf.Variable(tf.zeros([15, 1]))
wb2 = tf.matmul(layer1, w2) + b2
layer2 = tf.nn.relu(wb2)
# loss差异
loss = tf.reduce_mean(tf.square(y - layer2))  # y 真实 layer2 计算
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)  # 梯度下降
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(0, 10000):  # 训练1万次
        sess.run(train_step, feed_dict={x: dateNormal, y: priceNormal})
    # w1w2b1b2，A + wb -->layer2
    pred = sess.run(layer2, feed_dict={x: dateNormal})
    predPrice = np.zeros([15, 1])
    for i in range(0, 15):
        predPrice[i, 0] = (pred * 3000)[i, 0]
    plt.plot(date, predPrice, 'b', lw=1)
plt.show()

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/21904.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

编译原理 x - 练习题

编译原理 x - 练习题

简答题逆波兰后缀表达式和三元式序列源程序翻译成中间代码DAG优化正则文法 构造正则表达式正规式 改 上下文无关文法表示DFA有限状态机图移进-规约消除左递归文法-最左推导-短语LL(1)文法LR(0) | SLR(1)文法简答题 编译过程可分为前端和后端，描述一下前端和后端分别…
阅读更多...
【设计模式】装饰者模式：以造梦西游的例子讲解一下装饰者模式，这也是你的童年吗？

【设计模式】装饰者模式：以造梦西游的例子讲解一下装饰者模式，这也是你的童年吗？

文章目录1 概述1.1 问题1.2 定义1.3 结构1.4 类图2 例子2.1 代码2.2 效果图3 优点及适用场景3.1 优点3.2 适用场景1 概述 1.1 问题 众所周知，造梦西游3有四个角色，也就是师徒四人，这师徒四人每个人都有自己专属的武器和装备。假定我们以及设…
阅读更多...
推荐10个Vue 3.0开发的开源前端项目

推荐10个Vue 3.0开发的开源前端项目

Vue 是一款用于构建用户界面的 JavaScript 框，它基于标准 的HTML、CSS 和 JavaScript 构建，并提供了一套声明式的、组件化的编程模型，用以帮助开发者高效地开发用户界面。目前，Vue 3.0正式版也发布了两年的时间，越累越多的开发者也用上了Vue 3.0。 对比Vue2.x，Vue 3.0在…
阅读更多...
并发bug之源（二）-有序性

并发bug之源（二）-有序性

什么是有序性？ 简单来说，假设你写了下面的程序： java int a 1; int b 2; System.out.println(a); System.out.println(b);但经过编译器/CPU优化（指令重排序，和编程语言无关）后可能就变成了这样&#x…
阅读更多...
【DDR3 控制器设计】（7）DDR3 的用户端口读写模块设计

【DDR3 控制器设计】（7）DDR3 的用户端口读写模块设计

写在前面 本系列为 DDR3 控制器设计总结，此系列包含 DDR3 控制器相关设计：认识 MIG、初始化、读写操作、FIFO 接口等。通过此系列的学习可以加深对 DDR3 读写时序的理解以及 FIFO 接口设计等，附上汇总博客直达链接。 【DDR3 控制器设计】系列…
阅读更多...
CSS---复合选择器

CSS---复合选择器

目录 一：复合选择器的介绍 二、复合选择器的讲解 （1）后代选择器 （2）子元素选择器 （3）并集选择器 （4）链接伪类选择器 （5）focus伪类选择器 一&…
阅读更多...
基于SpringBoot的线上买菜系统

基于SpringBoot的线上买菜系统

末尾获取源码 开发语言：Java Java开发工具：JDK1.8 后端框架：SpringBoot 前端：采用JSP技术开发 数据库：MySQL5.7和Navicat管理工具结合 服务器：Tomcat8.5 开发软件：IDEA / Eclipse 是否Maven项目…
阅读更多...
【Spring系列】- Spring事务底层原理

【Spring系列】- Spring事务底层原理

Spring事务底层原理 😄生命不息，写作不止 🔥 继续踏上学习之路，学之分享笔记 👊 总有一天我也能像各位大佬一样 🏆 一个有梦有戏的人 怒放吧德德 🌝分享学习心得，欢迎指正&#xff0…
阅读更多...
Vue-CLI的安装、使用及环境配置（超详细）

Vue-CLI的安装、使用及环境配置（超详细）

Vue CLI 是一个基于 Vue 进行快速项目开发的工具。它可以提供可交互式的项目脚手架和运行时的服务依赖，帮助你快速完成一个风格统一、拓展性强的现代化 web 单页面应用。 Vue-CLI 所需环境 Vue-CLI 是一个需要全局安装的NPM包，安装需要在 Node.js 环境下…
阅读更多...
一、openCV+TensorFlow环境搭建

一、openCV+TensorFlow环境搭建

目录一、anaconda安装二、tensorflow安装三、Opencv安装四、pycharm新建项目使用Anaconda的环境五、验证环境安装六、tensorflow安装jupyter notebook一、anaconda安装 anaconda官网：https://www.anaconda.com/anaconda下载：https://repo.anaconda.com/…
阅读更多...
【k8s】10.网络插件

【k8s】10.网络插件

文章目录一、etcd详解1、etcd的特点2、准备签发证书的环境二、网络插件原理1、flannel1.1 UDP模式（性能差）1.2 VXLAN模式（性能较好）1.3 host-gw模式（性能最高）2、calico插件3、总结一、etcd详解 etcd是Cor…
阅读更多...
Redis_第二章_实战篇_第一节_ 短信登录

Redis_第二章_实战篇_第一节_ 短信登录

Redis_第二章_实战篇_第一节_ 短信登录 文章目录Redis_第二章_实战篇_第一节_ 短信登录短信登录1.1、导入黑马点评项目1.1.1 、导入SQL1.1.2、有关当前模型1.1.3、导入后端项目1.1.4、导入前端工程1.1.5 运行前端项目:1.2 、基于Session实现登录流程1.3 、实现发送短信验证码功…
阅读更多...
ANDI数据集介绍｜补充信息｜2022数维杯国际赛C题

ANDI数据集介绍｜补充信息｜2022数维杯国际赛C题

目录 1.患者基本信息 2.生物标记物量化值 3.认知评估 4.解剖结构量化值 5.Other 6.上述各信息的bl值 1.患者基本信息 RID (Participant roster ID) ex. 2、PTID (Original study protocol) ex. 011_S_0002、VISCODE (Visit code) ex. bl、SITE ex. 11、COLPROT (Study p…
阅读更多...
服务拆分和远程调用（微服务）

服务拆分和远程调用（微服务）

博客主页：踏风彡的博客 博主介绍：一枚在学习的大学生，希望在这里和各位一起学习。 所属专栏：SpringCloud 文章创作不易，期待各位朋友的互动，有什么学习问题都可在评论区留言或者私信我，我会尽我…
阅读更多...
课程设计 | 教学设备管理系统

课程设计 | 教学设备管理系统

🎈 作者：Linux猿 🎈 简介：CSDN博客专家🏆，华为云享专家🏆，Linux、C/C、云计算、物联网、面试、刷题、算法尽管咨询我，关注我，有问题私聊！ &…
阅读更多...
SpringCloud微服务（二）——Eureka服务注册中心

SpringCloud微服务（二）——Eureka服务注册中心

Eureka服务注册中心 SpringCloud组件，Eureka已停更。 内容简介 1、Eureka是什么 Eureka 是 Netflix 开发的，一个基于 REST 服务的，服务注册与发现的组件，以实现中间层服务器的负载平衡和故障转移。服务注册：将服务…
阅读更多...
[杂记]算法: 单调栈

[杂记]算法: 单调栈

0. 引言 单调栈, 顾名思义就是从栈底到栈顶元素单调递增或者单调递减的栈. 往往, 我们在解决寻找一个元素前面/后面的最远/最近处满足某条件的另一个元素的时候可以用到单调栈. 也是用两道算法题作为例子. 在这之前, 先简单写一下构造单调栈的模板. 如果我们需要从一个数组中…
阅读更多...
ES6 入门教程 18 Iterator 和 for...of 循环 18.7 for...of 循环

ES6 入门教程 18 Iterator 和 for...of 循环 18.7 for...of 循环

ES6 入门教程 ECMAScript 6 入门 作者：阮一峰 本文仅用于学习记录，不存在任何商业用途，如侵删 文章目录ES6 入门教程18 Iterator 和 for...of 循环18.7 for...of 循环18.7.1 数组18.7.2 Set 和 Map 结构18.7.3 计算生成的数据结构18.7.4 类似…
阅读更多...
供应叶酸PEG试剂Folic acid-PEG-Azide，FA-PEG-N3，叶酸-聚乙二醇-叠氮

供应叶酸PEG试剂Folic acid-PEG-Azide，FA-PEG-N3，叶酸-聚乙二醇-叠氮

1、名称 英文：Folic acid-PEG-Azide，FA-PEG-N3 中文：叶酸-聚乙二醇-叠氮 2、CAS编号：N/A 3、所属分类：Azide PEG Folic acid（FA） PEG 4、分子量：可定制，FA-PEG-N3 5…
阅读更多...
Web安全之CTF测试赛

Web安全之CTF测试赛

Web安全之CTF测试赛 1.000-我是谁 题目描述： 找到诈骗网站bsde.cn的域名注册人及邮箱，将域名注册人的126邮箱填写到下方答案框并点击送出 考察点：whois查询 whois查询网址： https://x.threatbook.com/ //微步在线 http://wh…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023