深入学习从入门到放弃：掌握梯度概念，开始征服深度学习！

文章目录

- - 从现实中的例子理解什么是梯度
  - 梯度的数学定义
  - - 梯度的严格的数学定义
    - 为什么梯度向量指向函数增长最快的方向？
  - 为什么梯度是深度学习优化的最基础概念
  - 在python中实现梯度求导的简单案例
  - - 一元线性回归
    - 多元线性回归
  - 结合示例深度学习中的梯度求导的一般过程
  - - 数学原理推导
    - 对应到代码中的梯度计算
  - 个人公众号

从现实中的例子理解什么是梯度

想象你在一座被浓雾笼罩的山上，想找到山谷的最低点。但由于能见度低，你无法看到全貌，只能感觉到脚下的坡度。这种坡度感告诉你哪个方向是向下的，哪边更陡峭。这个“坡度”就是梯度的直观表现，它指示了函数在当前点变化最快的方向和速率。此时，真想吟诗一首：

雾锁高山觅谷深，
脚踏迷途辨缓峻。
坡度指引下山路，
梯度犹似暗中灯。

梯度的数学定义

梯度的严格的数学定义

在多元微积分中，梯度（Gradient）是标量函数在某一点的方向导数取得最大值的方向。具体来说，对于一个实值的可微函数 $f(x_1, x_2, ..., x_n)$ ，其梯度是由函数对各个变量的偏导数组成的向量：
$\nabla f = \left( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n} \right)$

为什么梯度向量指向函数增长最快的方向？

首先，我们需要引入方向导数的概念。方向导数描述了函数在某个特定方向上的变化率。对于单位向量 $\mathbf{u}$ ，函数 $f$ 在点 $\mathbf{x}$ 沿方向 $\mathbf{u}$ 的方向导数定义为：

$D_{\mathbf{u}} f(\mathbf{x}) = \nabla f(\mathbf{x}) \cdot \mathbf{u} = \| \nabla f(\mathbf{x}) \| \cdot \| \mathbf{u} \| \cos \theta = \| \nabla f(\mathbf{x}) \| \cos \theta$

其中， $\theta$ 是 $\nabla f(\mathbf{x})$ 与 $\mathbf{u}$ 之间的夹角， $\| \cdot \|$ 表示向量的模。

从上式可以看出，方向导数 $D_{\mathbf{u}} f(\mathbf{x})$ 的值取决于 $\cos \theta$ 。当 $\theta = 0$ 时， $\cos \theta$ 取得最大值1，此时方向导数也达到最大值，即：

$D_{\mathbf{u}} f(\mathbf{x})_{\text{max}} = \| \nabla f(\mathbf{x}) \|$

这意味着，函数 $f$ 在点 $\mathbf{x}$ 沿着梯度方向 $\nabla f(\mathbf{x})$ ，具有最大的增长率。

为什么梯度是深度学习优化的最基础概念

梯度在深度学习中扮演着核心角色，几乎贯穿了整个模型训练和优化的过程。要理解梯度为何如此重要，需要从深度学习模型的构建、训练以及优化方法等多个角度来探讨。

1. 深度学习的目标：最小化损失函数

深度学习的核心目标是通过调整模型参数，使得模型在给定数据集上的损失函数达到最小值。损失函数（Loss Function）衡量了模型预测输出与真实标签之间的差距，是一个关于模型参数的多元函数。优化损失函数的过程本质上是一个在高维参数空间中寻找全局或局部最小值的问题。

2. 梯度提供了最陡下降的方向

在高维参数空间中，直接找到损失函数的最小值是极其困难的。然而，梯度为我们提供了一条捷径。梯度向量指示了损失函数在当前参数点处增长最快的方向。根据梯度的性质，沿着梯度的反方向，即是函数下降最快的路径。因此，梯度为我们提供了在参数空间中如何调整参数以最快速地降低损失函数值的指导。

3. 梯度下降法是深度学习的基础优化算法

梯度下降法（Gradient Descent）利用了梯度信息，通过迭代更新模型参数，使得每一步都朝着损失函数减小的方向前进。其基本更新公式为：

$\theta_{new} = \theta_{old} - \eta \nabla_{\theta} L(\theta_{old})$

其中， $\theta$ 表示模型参数， $\eta$ 是学习率， $L(\theta)$ 是损失函数， $\nabla_{\theta} L(\theta)$ 是损失函数对参数的梯度。

4. 反向传播算法依赖梯度计算

反向传播（Backpropagation）是训练神经网络的关键算法，用于高效地计算损失函数对每个参数的梯度。通过链式法则，反向传播将输出层的误差逐层传递回前面的网络层，计算出每个参数对损失的影响。这个过程的核心就是梯度的计算和传递，没有梯度，反向传播无法进行。

在python中实现梯度求导的简单案例

一元线性回归

下面示例展示了普通线性一元回归的梯度求导以及反向误差传播，并动态可视化其结果：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# 生成数据集
np.random.seed(0)
X = np.linspace(0, 10, 50)
y = 2 * X + 1 + np.random.randn(50) * 4  # 增加噪声强度

# 参数初始化
w, b = -10.0, -10.0  # 将初始参数设置为远离最优值
lr = 0.02  # 学习率
epochs = 300  # 训练次数

# 存储参数和损失以便绘图
ws, bs = [], []
losses = []

# 创建图形
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
scatter = ax1.scatter(X, y, color='blue', label='data scatter')
line, = ax1.plot([], [], 'r-', linewidth=2, label='fitted curve')
text_loss = ax1.text(0.05, 0.85, '', transform=ax1.transAxes, fontsize=12, verticalalignment='top')
ax1.set_xlabel('X')
ax1.set_ylabel('y')
ax1.set_title('simple Linear Regression')
ax1.legend()

ax2.set_xlim(0, epochs)
ax2.set_ylim(0, max((y - y.mean()) ** 2) * 1.2)
loss_line, = ax2.plot([], [], 'b-')
ax2.set_xlabel('epoch')
ax2.set_ylabel('loss')
ax2.set_title('loss curve')


def animate(i):
    global w, b
    y_pred = w * X + b
    loss = ((y_pred - y) ** 2).mean()

    # 计算梯度
    grad_w = 2 * ((y_pred - y) * X).mean()
    grad_b = 2 * (y_pred - y).mean()

    # 更新参数
    w -= lr * grad_w
    b -= lr * grad_b

    # 记录参数和损失
    ws.append(w)
    bs.append(b)
    losses.append(loss)

    # 更新拟合直线
    line.set_data(X, w * X + b)

    # 更新损失曲线
    loss_line.set_data(range(len(losses)), losses)

    # 更新损失文本
    text_loss.set_text(f'epoch: {i + 1}\ncurrent loss: {loss:.2f}')

    return line, loss_line, text_loss


# 初始化函数
def init():
    line.set_data([], [])
    loss_line.set_data([], [])
    text_loss.set_text('')
    return line, loss_line, text_loss


# 创建动画
ani = FuncAnimation(fig, animate, frames=epochs, init_func=init, interval=100, blit=True)
# 保存动画为 GIF 文件
ani.save('linear_regression_animation.gif', writer='pillow', fps=30)
plt.tight_layout()
plt.show()

在这里插入图片描述

多元线性回归

import numpy as np
import matplotlib.pyplot as plt

# 1. 生成数据集
np.random.seed(42)  # 设置随机种子以保证结果可重复

# 样本数量和特征数量
n_samples = 100
n_features = 5

# 生成随机特征矩阵 X，形状为 (100, 5)
X = np.random.randn(n_samples, n_features)

# 真实的权重和偏置，用于生成目标值 y
true_w = np.array([2, -3, 4, 1, -2])
true_b = 5

# 生成目标值 y，并添加一些噪声
y = X.dot(true_w) + true_b + np.random.randn(n_samples) * 0.5  # 噪声的标准差为 0.5

# 2. 参数初始化
w = np.zeros(n_features)  # 初始化权重为零向量
b = 0.0  # 初始化偏置为 0
lr = 0.01  # 学习率
epochs = 300  # 训练轮数

# 存储损失值以便绘图
losses = []

# 3. 训练过程
for epoch in range(epochs):
    # 前向传播：计算预测值
    y_pred = X.dot(w) + b

    # 计算损失（均方误差）
    loss = ((y_pred - y) ** 2).mean()
    losses.append(loss)

    # 计算梯度
    grad_w = 2 * X.T.dot(y_pred - y) / n_samples
    grad_b = 2 * (y_pred - y).mean()

    # 参数更新
    w -= lr * grad_w
    b -= lr * grad_b

    # 可选：每隔一定迭代次数打印一次损失值
    if (epoch + 1) % 50 == 0:
        print(f"Epoch {epoch + 1}/{epochs}, Loss: {loss:.4f}")

# 4. 绘制损失曲线
plt.figure(figsize=(8, 6))
plt.plot(range(1, epochs + 1), losses, label='train loss')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('multiple linear regression loss')
plt.legend()
plt.grid(True)
plt.show()

# 5. 打印最终的参数值
print("训练结束后的参数值：")
print(f"w: {w}")
print(f"b: {b}")

# 6. 比较真实参数和模型学习到的参数
print("\n真实的参数值：")
print(f"true_w: {true_w}")
print(f"true_b: {true_b}")

程序输出：

Epoch 50/300, Loss: 9.0096
Epoch 100/300, Loss: 1.7507
Epoch 150/300, Loss: 0.4893
Epoch 200/300, Loss: 0.2570
Epoch 250/300, Loss: 0.2122
Epoch 300/300, Loss: 0.2032
训练结束后的参数值：
w: [ 2.0363504  -2.90204453  3.95529038  1.08716601 -2.00416486]
b: 4.896948074085842
真实的参数值：
true_w: [ 2 -3  4  1 -2]
true_b: 5

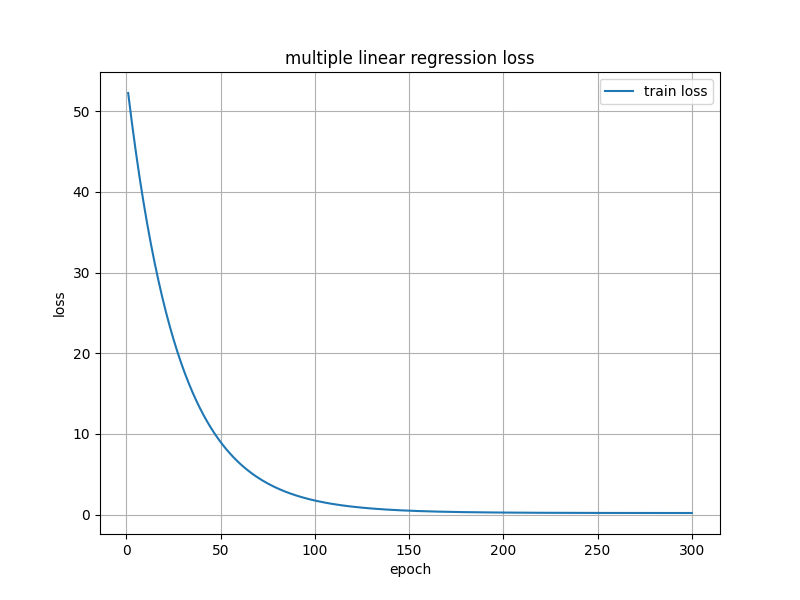
以及loss的下降曲线图：

结合示例深度学习中的梯度求导的一般过程

数学原理推导

1. 问题背景

在上面的多元线性回归案例中，我们的目标是找到最优的参数 $\mathbf{w}$ 和 $b$ ，使得模型预测值 $\hat{\mathbf{y}}$ 与真实值 $\mathbf{y}$ 之间的均方误差（Mean Squared Error, MSE）最小化。

模型表示：

$\hat{\mathbf{y}} = \mathbf{X} \mathbf{w} + b$

$\mathbf{X}$ ：形状为 $(n, m)$ 的数据矩阵， $n$ 为样本数， $m$ 为特征数。
$\mathbf{w}$ ：形状为 $(m, 1)$ 的权重向量。
$b$ ：偏置项，标量。

损失函数（MSE）：

$L(\mathbf{w}, b) = \frac{1}{n} \sum_{i=1}^n (\hat{y}_i - y_i)^2$

2. 计算梯度

我们需要计算损失函数 $L$ 对参数 $\mathbf{w}$ 和 $b$ 的梯度，即 $\nabla_{\mathbf{w}} L$ 和 $\frac{\partial L}{\partial b}$ 。

2.1. 对 $\mathbf{w}$ 的梯度 $\nabla_{\mathbf{w}} L$

步骤1：展开损失函数

$L(\mathbf{w}, b) = \frac{1}{n} \sum_{i=1}^n (\hat{y}_i - y_i)^2 = \frac{1}{n} \sum_{i=1}^n (\mathbf{x}_i^\top \mathbf{w} + b - y_i)^2$

其中， $\mathbf{x}_i$ 是第 $i$ 个样本的特征向量。

步骤2：对 $\mathbf{w}$ 求偏导

对 $\mathbf{w}$ 求梯度：

$\nabla_{\mathbf{w}} L = \frac{\partial L}{\partial \mathbf{w}} = \frac{\partial}{\partial \mathbf{w}} \left( \frac{1}{n} \sum_{i=1}^n (\mathbf{x}_i^\top \mathbf{w} + b - y_i)^2 \right)$

由于求和和求导可以交换：

$\nabla_{\mathbf{w}} L = \frac{1}{n} \sum_{i=1}^n \frac{\partial}{\partial \mathbf{w}} \left( (\mathbf{x}_i^\top \mathbf{w} + b - y_i)^2 \right)$

步骤3：计算单个项的偏导

对每个 $i$ ，应用链式法则：

$\frac{\partial}{\partial \mathbf{w}} \left( (\mathbf{x}_i^\top \mathbf{w} + b - y_i)^2 \right) = 2 (\mathbf{x}_i^\top \mathbf{w} + b - y_i) \frac{\partial}{\partial \mathbf{w}} (\mathbf{x}_i^\top \mathbf{w})$

注意到 $\frac{\partial}{\partial \mathbf{w}} (\mathbf{x}_i^\top \mathbf{w}) = \mathbf{x}_i$ ，因此：

$\frac{\partial}{\partial \mathbf{w}} \left( (\mathbf{x}_i^\top \mathbf{w} + b - y_i)^2 \right) = 2 (\mathbf{x}_i^\top \mathbf{w} + b - y_i) \mathbf{x}_i$

步骤4：合并梯度表达式

将所有样本的梯度相加：

$\nabla_{\mathbf{w}} L = \frac{2}{n} \sum_{i=1}^n (\hat{y}_i - y_i) \mathbf{x}_i$

将上述求和形式转换为矩阵形式。定义误差向量：

$\mathbf{e} = \hat{\mathbf{y}} - \mathbf{y}$

将样本特征矩阵 $\mathbf{X}$ 的转置 $\mathbf{X}^\top$ 与误差向量相乘：

$\nabla_{\mathbf{w}} L = \frac{2}{n} \mathbf{X}^\top (\hat{\mathbf{y}} - \mathbf{y}) = \frac{2}{n} \mathbf{X}^\top \mathbf{e}$

2.2. 对 $b$ 的梯度 $\frac{\partial L}{\partial b}$

步骤1：对 $b$ 求偏导

$\frac{\partial L}{\partial b} = \frac{\partial}{\partial b} \left( \frac{1}{n} \sum_{i=1}^n (\mathbf{x}_i^\top \mathbf{w} + b - y_i)^2 \right) = \frac{1}{n} \sum_{i=1}^n \frac{\partial}{\partial b} \left( (\mathbf{x}_i^\top \mathbf{w} + b - y_i)^2 \right)$

步骤2：计算单个项的偏导

$\frac{\partial}{\partial b} \left( (\mathbf{x}_i^\top \mathbf{w} + b - y_i)^2 \right) = 2 (\mathbf{x}_i^\top \mathbf{w} + b - y_i) \frac{\partial}{\partial b} (\mathbf{x}_i^\top \mathbf{w} + b - y_i)$

由于 $\frac{\partial}{\partial b} (\mathbf{x}_i^\top \mathbf{w} + b - y_i) = 1$ ，因此：

$\frac{\partial}{\partial b} \left( (\mathbf{x}_i^\top \mathbf{w} + b - y_i)^2 \right) = 2 (\mathbf{x}_i^\top \mathbf{w} + b - y_i)$

步骤3：合并梯度表达式

$\frac{\partial L}{\partial b} = \frac{2}{n} \sum_{i=1}^n (\hat{y}_i - y_i) = \frac{2}{n} \sum_{i=1}^n e_i = 2 \cdot \text{mean}(\hat{\mathbf{y}} - \mathbf{y})$

对应到代码中的梯度计算

在代码中：

grad_w = 2 * X.T.dot(y_pred - y) / len(y)
grad_b = 2 * (y_pred - y).mean()

X.T.dot(y_pred - y)对应于 $\mathbf{X}^\top (\hat{\mathbf{y}} - \mathbf{y})$ 。
len(y)是样本数量 $n$ 。
(y_pred - y).mean()对应于误差的平均值 $\text{mean}(\hat{\mathbf{y}} - \mathbf{y})$ 。

对比数学推导和代码如下：

对于 $\nabla_{\mathbf{w}} L$ ：

数学上：

$\nabla_{\mathbf{w}} L = \frac{2}{n} \mathbf{X}^\top (\hat{\mathbf{y}} - \mathbf{y})$

代码中：
```
grad_w = 2 * X.T.dot(y_pred - y) / len(y)
```
二者完全一致。
对于 $\frac{\partial L}{\partial b}$ ：

数学上：

$\frac{\partial L}{\partial b} = 2 \cdot \text{mean}(\hat{\mathbf{y}} - \mathbf{y})$

代码中：
```
grad_b = 2 * (y_pred - y).mean()
```
也完全一致。