摘要
多机器人路径规划在现代自动化、仓储管理及智能交通系统中有着广泛的应用。本文提出了一种基于A*算法的多机器人路径规划方法,旨在解决多机器人在同一环境中的路径冲突问题。通过采用启发式搜索和路径优化策略,机器人能够在保持避障的前提下实现最优路径规划。实验结果表明,该方法在复杂环境中能够有效降低机器人路径规划的时间复杂度,并避免机器人之间的碰撞。
理论
多机器人路径规划(Multi-Robot Path Planning, MRPP)是机器人学中的一个重要问题,其核心目标是在多机器人系统中为每个机器人规划一条从起点到终点的无碰撞路径。常见的路径规划算法包括Dijkstra算法、A*算法以及其改进版。为了实现多机器人路径规划,需要解决以下问题:
-
避障问题:规划路径必须确保机器人不会与环境中的障碍物相撞。
-
避免路径冲突:多个机器人在同一时间段内可能会经过同一地点,需采用策略避免冲突。
-
全局最优性:算法不仅需要为单个机器人规划最优路径,还需要在系统层面保证多机器人路径的整体最优性。
A*算法是一种经典的启发式搜索算法,在路径规划中表现出色。其核心思想是通过启发函数 𝑓(𝑛)=𝑔(𝑛)+ℎ(𝑛),其中𝑔(𝑛)为起点到节点,𝑛的实际代价, ℎ(𝑛)为节点,𝑛到终点的启发式估计代价。对于多机器人系统,可以通过优先考虑时间顺序以及空间区域的方式,保证多个机器人能够协调前进。
实验结果
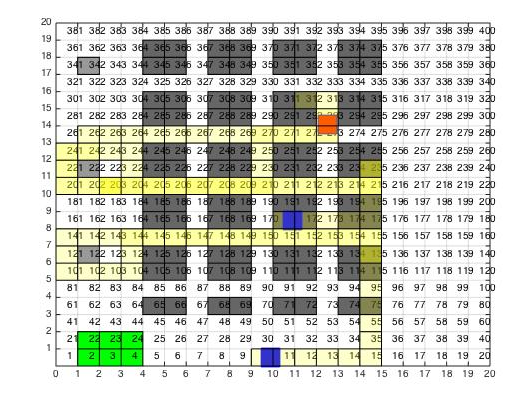
实验通过MATLAB对多机器人路径规划进行了仿真。设置一个20x20的网格地图,黑色区域代表障碍物,绿色为机器人起始点,黄色为规划出的机器人路径,红色为终点。多个机器人在路径规划过程中能够避免与障碍物及其他机器人碰撞。
仿真结果表明,使用A*算法能够为每个机器人有效地规划路径,并在一定时间内完成多机器人的路径规划,避免了机器人的路径冲突。
部分代码
% 初始化地图
map = zeros(20,20); % 创建20x20地图
map(1:3,1:5) = 1; % 设置障碍物
map(6:10,10) = 1; % 更多障碍物
% 定义机器人起点和终点
start = [2, 1]; % 机器人1起点
goal = [14, 14]; % 机器人1终点
% 调用A*算法函数
path = Astar(map, start, goal);
% 显示结果
figure;
imshow(map, 'InitialMagnification', 'fit');
hold on;
plot(path(:,2), path(:,1), 'r', 'LineWidth', 2); % 绘制路径
hold off;
% A*算法实现
function path = Astar(map, start, goal)
% 初始化
[rows, cols] = size(map);
open_list = [];
closed_list = zeros(rows, cols);
% 将起点放入open_list
open_list = [open_list; start, 0, heuristic(start, goal)];
while ~isempty(open_list)
% 找到当前开销最低的节点
[~, idx] = min(open_list(:, 3));
current = open_list(idx, :);
open_list(idx, :) = []; % 从open_list中删除
% 检查是否到达目标
if isequal(current(1:2), goal)
path = reconstruct_path(current);
return;
end
% 获取邻居节点
neighbors = get_neighbors(current(1:2), rows, cols);
for i = 1:size(neighbors, 1)
neighbor = neighbors(i, :);
if map(neighbor(1), neighbor(2)) == 1 || closed_list(neighbor(1), neighbor(2))
continue; % 忽略障碍物和已访问节点
end
tentative_g = current(4) + 1; % 假设代价为1
open_list = [open_list; neighbor, tentative_g, tentative_g + heuristic(neighbor, goal)];
end
closed_list(current(1), current(2)) = 1; % 标记已访问
end
error('无法找到路径');
end
% 启发函数(曼哈顿距离)
function h = heuristic(pos, goal)
h = abs(pos(1) - goal(1)) + abs(pos(2) - goal(2));
end
% 生成邻居节点
function neighbors = get_neighbors(pos, rows, cols)
directions = [0 1; 1 0; 0 -1; -1 0];
neighbors = [];
for i = 1:4
new_pos = pos + directions(i, :);
if new_pos(1) > 0 && new_pos(1) <= rows && new_pos(2) > 0 && new_pos(2) <= cols
neighbors = [neighbors; new_pos];
end
end
end
% 重建路径
function path = reconstruct_path(current)
path = current(1:2);
end
参考文献
❝
Silver, D., "Cooperative Pathfinding," AI Game Programming Wisdom 3, 2006.
Hart, P. E., Nilsson, N. J., & Raphael, B., "A Formal Basis for the Heuristic Determination of Minimum Cost Paths," IEEE Transactions on Systems Science and Cybernetics, 1968.
LaValle, S. M., "Planning Algorithms," Cambridge University Press, 2006.