目录
1 主要内容
模型示意图
目标函数
程序亮点
2 部分程序
3 程序结果
4 下载链接
1 主要内容
本程序基本复现《“碳中和”目标下电气互联系统有功-无功协同优化模型》,文献模型提供了一个很好的创新思路,把常规电气互联系统的调度和有功无功优化结合起来,增加可再生能源无功、电容器、SVC、OLTC等调节设备,采用二阶锥松弛法对配网模型非线性约束进行凸松弛,采用大M法对离散无功补偿装置的投切容量进行线性化表达,将模型转换为混合整数二阶锥规划问题 进行求解,程序采用matlab+gurobi(cplex)进行求解,注释清晰,方便研究借鉴!

-
模型示意图

注意:本程序采用以修改的IEEE33节点配电网和比利时20节点配气网耦合形成的电气互联系统作为测试算例,虽然设备安装位置以及参数和文献会存在细微差别,但是文献中的设备模型以及约束内容基本实现,是个很好的学习资料。
-
目标函数
采用购电成本最小和网损最小为目标,并增加电压偏差最小作为可选项(由于非线性,需要采用gurobi才能求解此目标),其他两个采用cplex即可求解。
目标函数代码:
%%%% PDN 购电成本最小
Ele_price = [361.28 333.13 304.97 286.75 264.18 292.15 433.93 683.00 863.30 784.88 629.56 556.88 ...
533.63 517.60 489.99 470.52 521.10 709.54 1010.67 1213.17 1178.29 930.13 614.56 439.71]; % 24h电价 元/MW*h
Ele_price = Ele_price * 1e4; % 元/p.u.*h
Obj_grid = Ele_price * Pgrid';
%%%% 网损最小
for t = 1:24
Obj_Ploss24(t) = sum(I2(1:32,t) .* R); %
end
Obj_Ploss = sum(Obj_Ploss24);
%%%% 电压偏差最小
% Obj_Vol = sum(sum(U2 - 1.05^2*ones(33,24))); % 电压偏差要用 gurobi gap设定才易求解
-
程序亮点
- 程序整体比较大,有500余行,包括潮流约束、设备出力约束、无功约束以及线性化部分,涵盖内容比较广泛,学习的“料”够足。
- 最近很多咨询答疑讲解的,这种较大的模型会专门录制讲解视频,敬请期待。
2 部分程序
% 二阶锥约束,数学表达式是转换成标准二阶锥,此处用一般形式,方便编程
Cons_SOC = [Cons_SOC, I2 .* U2(L_i,:) >= P.^2 + Q.^2];
for t = 1:NT
for i = 1:NL
%%%%% 含 离散电容器组 的相关约束
if ~isempty(find(Ind_ComCap == L_j(i))) % 安装补偿电容
Cj_count(t) = Cj_count(t) + 1;
% 式 28 delta:σ 式中Ci_min那儿少写了一个uj
Cons_Q = [Cons_Q, Q(i,t) - X(i)*I2(i,t) + ...
0.5*(U2(L_j(i),t)*Cj_min(Cj_count(t),1) + Sj(Cj_count(t))*(2^0*dlt{Cj_count(t)}(1,t) + 2^1*dlt{Cj_count(t)}(2,t) + 2^2*dlt{Cj_count(t)}(3,t))) + ...
Qg_SVC(L_j(i),t) ...
== QkidLine(i,t) + Qd(L_j(i),t)];
for m = 1:v+1 % 含离散电容补偿的电压线性化约束 Eq38
Cons_U = [Cons_U, U2(L_j(i),t) - M*(1-xd{Cj_count(t)}(m,t)) <= dlt{Cj_count(t)}(m,t) <= U2(L_j(i),t) + M*(1-xd{Cj_count(t)}(m,t))];
Cons_U = [Cons_U, -M*xd{Cj_count(t)}(m,t) <= dlt{Cj_count(t)}(m,t) <= M*xd{Cj_count(t)}(m,t)];
end
Cons_U = [Cons_U, 0 <= ... % Eq39
2^0*xd{Cj_count(t)}(1,t)+ 2^1*xd{Cj_count(t)}(2,t) + 2^2*xd{Cj_count(t)}(3,t) ...
<= (Cj_max(Cj_count(t),1) - Cj_min(Cj_count(t),1))/Sj(Cj_count(t),1)];
else % 未安装补偿电容 的 无功平衡约束
Cons_Q = [Cons_Q, Q(i,t) - X(i)*I2(i,t) + Qg_SVC(L_j(i),t) + Qg_WT(L_j(i),:) == QkidLine(i,t) + Qd(L_j(i),t)];
end
%%%%% 含 OLTC 的相关约束
if ~isempty(find(Ind_OLTC == i)) % 含OTLC的支路的线性化约束
OTLC_count(t) = OTLC_count(t)+1; % t时刻 第1个OLTC, 第2个OlTC
Cons_U = [Cons_U, sum(y_j{OTLC_count(t)}(:,t)./T_OLTC(:,t).^2,1) == U2(L_i(i),t) - (R(i)*P(i,t) + X(i)*Q(i,t))]; % OLTC所在支路电压差
% 以下为OLTC相关约束
for k = 1:n_OLTC
Cons_U = [Cons_U, -M*(1-e_ij{OTLC_count(t)}(k,t)) + U2(L_j(i),t) <= y_j{OTLC_count(t)}(k,t) <= U2(L_j(i),t) + M*(1-e_ij{OTLC_count(t)}(k,t))];
Cons_U = [Cons_U, -M*e_ij{OTLC_count(t)}(k,t) <= y_j{OTLC_count(t)}(k,t)<= M*e_ij{OTLC_count(t)}(k,t)];
end
Cons_U = [Cons_U,sum(e_ij{OTLC_count(t)}(:,t),1) == 1]; % 某一时刻 在11个档位中,只能有一个为1
else
% 不含OTLC的支路
Cons_U = [Cons_U, U2(L_j(i),t)== U2(L_i(i),t) - 2*(R(i)*P(i,t)+X(i)*Q(i,t)) + (R(i)^2+X(i)^2)*I2(i,t)];
end
end
end
% 一些边界约束
Cons_P = [Cons_P, repmat(Pmin,1,24) <= P <= repmat(Pmax,1,24)]; % 线路潮流约束
Cons_P = [Cons_P, WT_Pg_min <= Pg_WT <= WT_Pg_max]; % 风机出力有功P上下限约束
Cons_P = [Cons_P, PV_Pg_min <= Pg_PV <= PV_Pg_max]; % 光伏出力有功P上下限约束
Cons_Q = [Cons_Q, Qg_WT_min <= Qg_WT <= Qg_WT_max]; % 风机出力无功P上下限约束
Cons_Q = [Cons_Q, repmat(SVC_min,1,24) <= Qg_SVC(Ind_SVC,:) <= repmat(SVC_max,1,24)]; % 安装了SVC节点, 将 Qg_SVC出力限定在 上下限内
Cons_U = [Cons_U, U2_min <= U2 <= U2_max]; % 节点电压 上下限约束
% Cons_P = [Cons_P, Pgrid >= 0];
Cons_Q = [Cons_Q, Qgrid >= 0];
Cons_I = [Cons_I, I2 >= 0 ];
% GDN 约束条件
Cons_GDN = [];
alpha = repmat(alpha_Cmn,1,24);
%%%% 气流平衡约束 + A_GS*(GasStorge_out-GasStorge_in)
Cons_GDN = [Cons_GDN, A_GW*GasWell - A_GP*GasFlow - A_GC*(alpha.*GasComp) - A_GT_GDN*GasGT- Gas_Demand == zeros(20,24)]; %
%%%% 气流-气压耦合约束 转为 二阶锥约束
Cons_GDN = [Cons_GDN, GasFlow.^2 <= repmat(K_Pipe.^2,1,24) .* GasPre(P_m,:) - repmat(K_Pipe.^2,1,24) .*GasPre(P_n,:) ];
%%%% 节点气压 约束
Cons_GDN = [Cons_GDN, GasPre(P_m,:) >= GasPre(P_n,:)]; % GDN中气流方向预定, 从上至下, 故气压首端大于末端
gama = repmat(gama_Cmn,1,24);
Cons_GDN = [Cons_GDN, GasPre(Comp_n,:) <= gama .* GasPre(Comp_m,:)]; % 压缩机两端气压
Cons_GDN = [Cons_GDN,repmat(Pre_min.^2,1,24) <= GasPre <= repmat(Pre_max.^2,1,24)]; % 所有节点气压的边界约束
%%%%% 各天然气源出力 约束
Cons_GDN = [Cons_GDN,zeros(n_GW,24) <= GasWell <= repmat(G_GW_max,1,24)]; % 气源上下限/ kcf
%%%% 各管道流量约束
Cons_GDN = [Cons_GDN, 0 <= GasFlow <= 100];
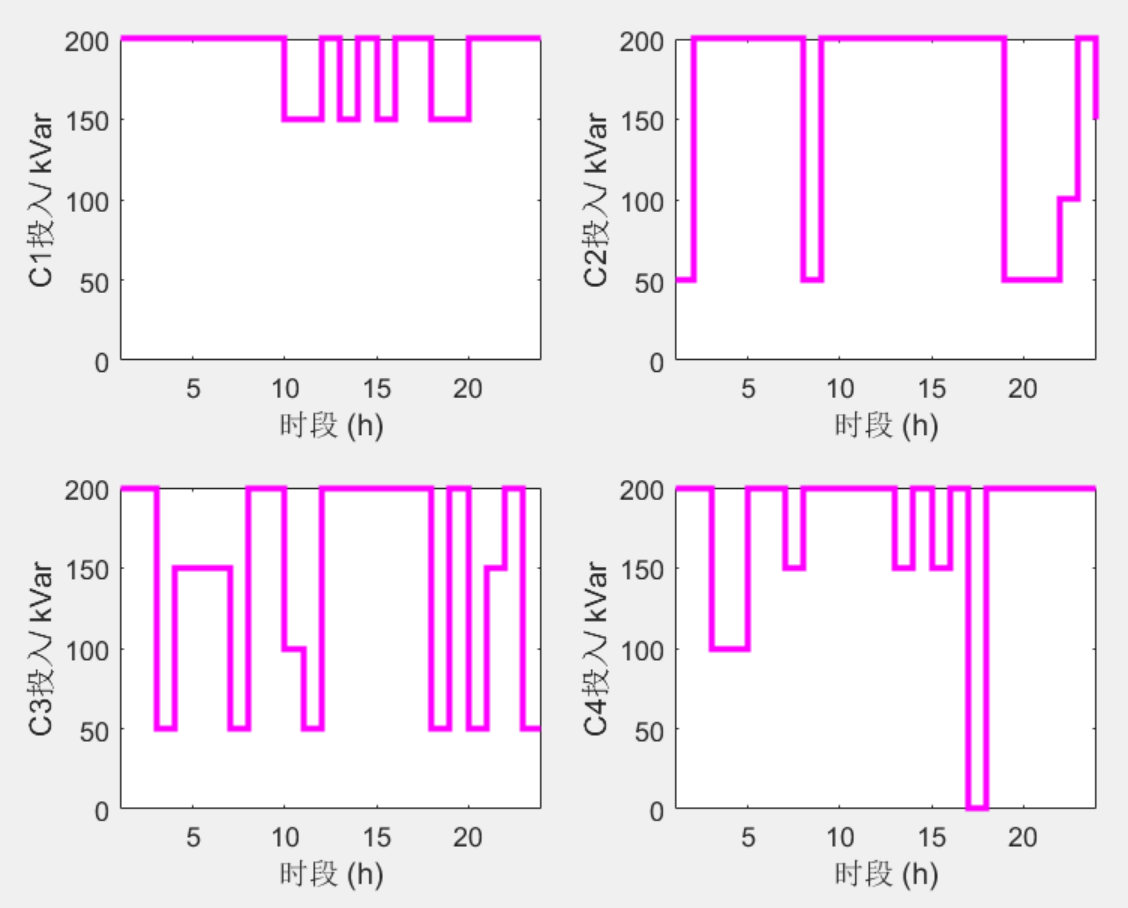
3 程序结果








![[Meachines] [Easy] Sea WonderCMS-XSS-RCE+System Monitor 命令注入](https://img-blog.csdnimg.cn/img_convert/8e94931c60b24ef99f4ec3cab6db2c86.jpeg)