目录
前言:
复写零
题目解析
算法原理
算法编写
四数之和
题目解析
算法原理
算法编写
前言:
本文是双指针算法的最后一文,以复写零和四数之和作为结束,介绍方式同样是题目解析,算法原理,算法编写三部曲,以下是题目的链接:
1089. 复写零 - 力扣(LeetCode)
18. 4Sum - 力扣(LeetCode)
那么话不多说,直接进入主题。
复写零
题目解析


题目的要求就是,在原来的数组基础上(不允许另外创建一个数组),调用了函数,原来是零的地方,写两次,并且不能影响后面的元素,除非是已经超过了数组的空间。题目的要求还是比较简单的。
那么这道题存不存在暴力解法呢?
显然,这道题并不是通过n个循环就可以解决的,所以我们不妨直接使用双指针。
到这个阶段,不妨不用思考为什么使用双指针,因为目前来说算法基础并不牢靠,我们不妨积累经验。
算法原理
我们不妨模拟一下这个复写零的过程:

cur指向的是原来的数组,我们假设条件就地修改这个条件不存在,我们如果是新开一块空间,过程就是两个for遍历数组,如果不是0,cur dest都++,如果是0,cur++,dest++两次,这是原来的过程,最后结束条件就是判断dest是否到了结束位置。
在这个过程,我们要考虑一个点就是dest如果是碰见了0进行复写,第二个零越界了怎么办?
这个情况我们只需要将原数组的最后一个位置置为零即可,虽然越界,但是是因为复写,此时最后置为零就完全没问题了。
那么为什么我们要模拟这过程呢?
因为我们要找到最后一个复写的数,如果找不到,我们没有办法进行后续的复写操作。
第一步也就完成了,找到复写的最后一个数,最后开始复写。
开始复写的判断结束条件就是cur是否走到了-1,判断arr[cur]是否为0,是0dest就多走一步,不是就走一步,别看说着轻松,有许多要注意的。
算法编写
class Solution
{
public:
void duplicateZeros(vector<int>& arr)
{
//找到最后一个复写的数
int cur = 0,dest = -1;
while(cur < arr.size())
{
if(arr[cur]) dest++;
else dest += 2;
//边界验证的辅助条件
if(dest >= arr.size() - 1) break;
cur++;
}
//处理边界情况 并且进行第一步复写
if(dest == arr.size())
{
arr[dest - 1] = 0;
dest -= 2,cur--;
}
//进行复写
while(cur >= 0)
{
if(arr[cur]) arr[dest--] = arr[cur];
else arr[dest--] = 0,arr[dest--] = 0;
cur--;
}
}
};第一个点,为什么dest要从-1开始,因为cur要先判断,判断之后dest才走,如果一开始dest就在0位置,那么就相当于多走了一步,我们拿数组[0]举例,如果dest在0位,那么走两步,最后的位置是2,已经完全超过了我们预期的判断位置,即便是越界,越的也应该是1这个位置。
第二个点,处理边界的时候,dest和cur需要移动,因为这已经是一次复写了。
第三个点,复写的时候,if(arr[cur])里面的cur是不可以--的,因为后面会用到当前的cur。
这几个小细节注意点为好。
此时这道题就做完了,时间复杂度呢是O(N),空间复杂度为O(1)。
四数之和
题目解析


题目的意思和三数之和十分像的,三数之和是找三个数等于0,那么该题目是找4个数字等于target,并且下标不能重复,也就是一个数字不能一直使用,题目的要求很简单,所以我们直接进入算法原理部分。
算法原理
原理和三数之和是十分像的,我们只需要固定个数,然后找三个数和该数 - target相等,再固定一个数,找两个数,等于target - 两外两个数,这就是妥妥的双指针了,根本不需要经过思考就可以动手了,其次就是去重操作,就没有了。
算法编写
class Solution
{
public:
vector<vector<int>> fourSum(vector<int>& nums, int target)
{
sort(nums.begin(),nums.end());
vector<vector<int>> ans;
for(int i = nums.size() - 1;i > 2;)
{
for(int j = i - 1;j > 1;)
{
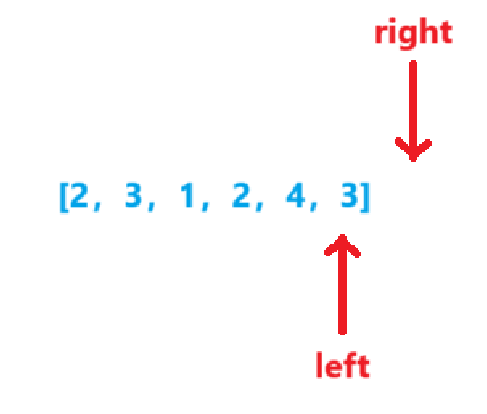
int left = 0, right = j - 1;
while(left < right)
{
long long sum = (long long)nums[j] + (long long)nums[left] + (long long)nums[right] + (long long)nums[i];
if( sum == (long long)target)
{
ans.push_back({nums[i],nums[j],nums[left++],nums[right--]});
while(left < right && nums[left] == nums[left - 1]) left++;
while(left < right && nums[right] == nums[right + 1]) right--;
}
else if(sum > (long long)target)
right--;
else left++;
}
j--;
while(j > 1 && nums[j] == nums[j + 1]) j--;
}
i--;
while(i > 2 && nums[i] == nums[i + 1]) i--;
}
return ans;
}
};至于为什么使用long long,因为:
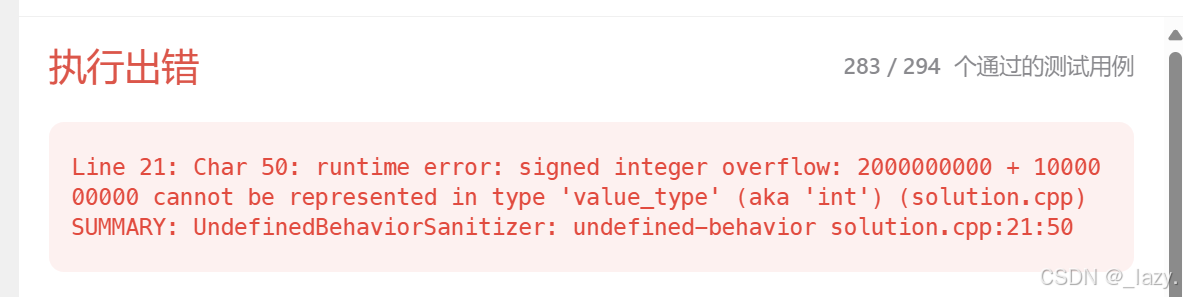
这个题目较为恶心的是,,存在int溢出的风险。
双指针算法也就到这里啦,后面的是滑动窗口~
感谢阅读!