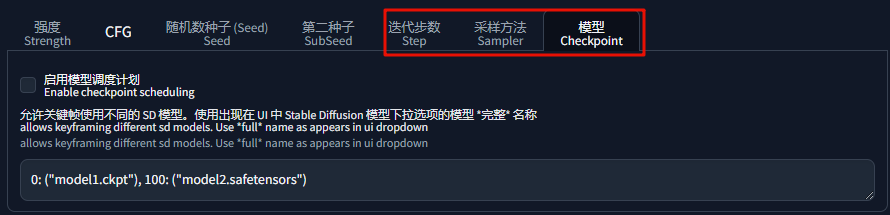
对于查询区间和的问题,可以预处理出来一个前缀和数组 dp,数组中存储的是从下标 0 的位置到当前位置的区间和,这样只需要通过前缀和数组就可以快速的求出指定区间的和了,例如求 l ~ r 区间的和,就可以之间使用 dp[l - 1] - dp[r] 来计算
1. DP34 【模板】前缀和
DP34 【模板】前缀和
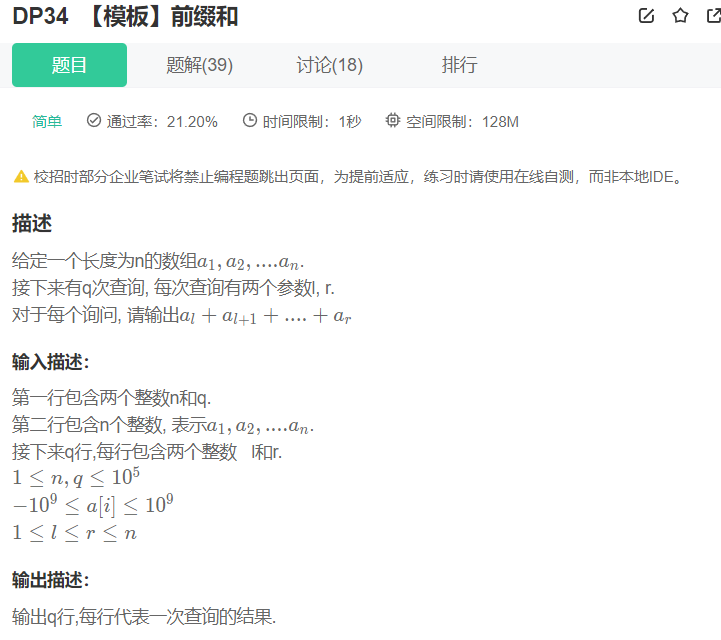
这里从下标 1 开始填是为了在初始化前缀和数组时更方便
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int p = sc.nextInt();
int[] arr = new int[N + 1];
long[] dp = new long[N + 1];
for (int i = 1; i <= N; i++) {
arr[i] = sc.nextInt();
}
for (int i = 1; i <= N; i++) {
dp[i] = dp[i - 1] + arr[i];
}
int l = 0, r = 0;
while (p-- != 0) {
l = sc.nextInt();
r = sc.nextInt();
System.out.println(dp[r] - dp[l - 1]);
}
}
}2. DP35 【模板】二维前缀和
二维前缀和模版

和一维的前缀和数组类似,这里需要先预处理出来一个前缀和矩阵 dp[][],dp[i][j] 就表示从(1,1)到(i,j)这个矩阵中的所有元素的和
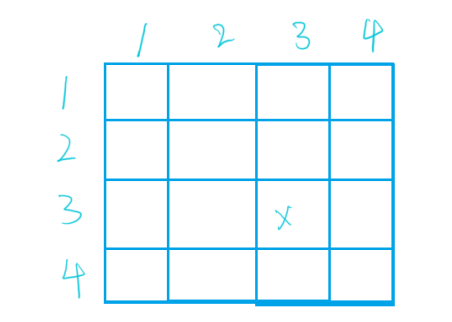
放到矩阵中可以看出,如果想要求(1,1)到(i,j)区间内的区域和,需要先加上 A,B,C,D 四个区域的和,如果单独的表示 B 区域或者 C 并不好表示,但是 A + B 和 A + C 是很好表示的,把这两个区域加起来再减去多加的 A ,再加上 D 就是整个区域的和

得到了前缀和数组之后,该怎么去使用呢?
如果说给出了(x1,y1)(x2,y2)两个点,那么就是求红色框的元素的和
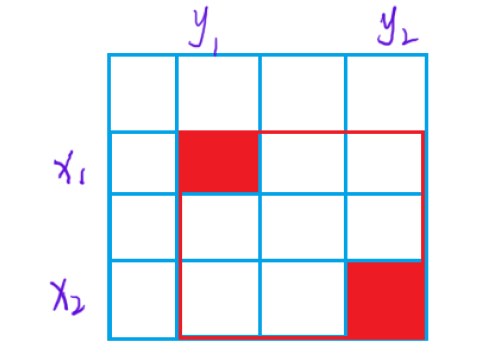
也就是求出 D 区域的和,由于 B 和 C 并不好单独转换,就可以转化为 A+B+C+D 的值先减去 A+B 的值,再减去 A + C 的值,此时方法 A 被多减了一次,再加上就是 D 区域的和了
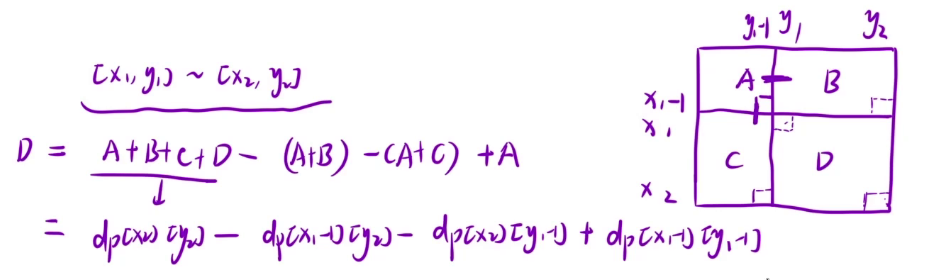
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), m = sc.nextInt();
int q = sc.nextInt();
int[][] A = new int[n + 1][m + 1];
long[][] dp = new long[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
A[i][j] = sc.nextInt();
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
dp[i][j] = dp[i][j - 1] + dp[i - 1][j] - dp[i - 1][j - 1]+ A[i][j];
}
}
int x1 = 0,y1 = 0,x2 = 0,y2 = 0;
while (q-- != 0) {
x1 = sc.nextInt();
y1 = sc.nextInt();
x2 = sc.nextInt();
y2 = sc.nextInt();
System.out.println(dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1]);
}
}
}3. 寻找数组的中心下标
724. 寻找数组的中心下标

根据题目要求就是求 0~ i - 1区间的和是否和区间 i + 1~n - 1 的和相等,那么此题dp[i] 就表示的是[0,i-1] 区间的和而不是之前的 0 ~ i 区间的和了,相应的,状态转移方程也要有所变化
同时这道题还需要求一个后缀和数组用来描述后半段的区间和,也是同样的道理,只不过 dp[i] 表示的是[i + 1,n - 1] 区间的和,这段区间的状态转移方程也就是 dp[i+1] + nums[i + 1]

class Solution {
public int pivotIndex(int[] nums) {
int n = nums.length;
int[] dp = new int[n];
int[] g = new int[n];
for (int i = 1; i < n; i++) {
dp[i] = dp[i - 1] + nums[i - 1];
}
for (int i = n - 2; i >= 0; i--) {
g[i] = g[i + 1] + nums[i + 1];
}
for (int i = 0; i < n; i++) {
if (g[i] == dp[i]) {
return i;
}
}
return -1;
}
}4. 除自身以外数组的乘积
238. 除自身以外数组的乘积

这道题其实就和上道题非常类似,把 i 位置之前的数都求一个前缀积,之后的数求一个后缀积,只需要把前缀积和后缀积相乘就可以了
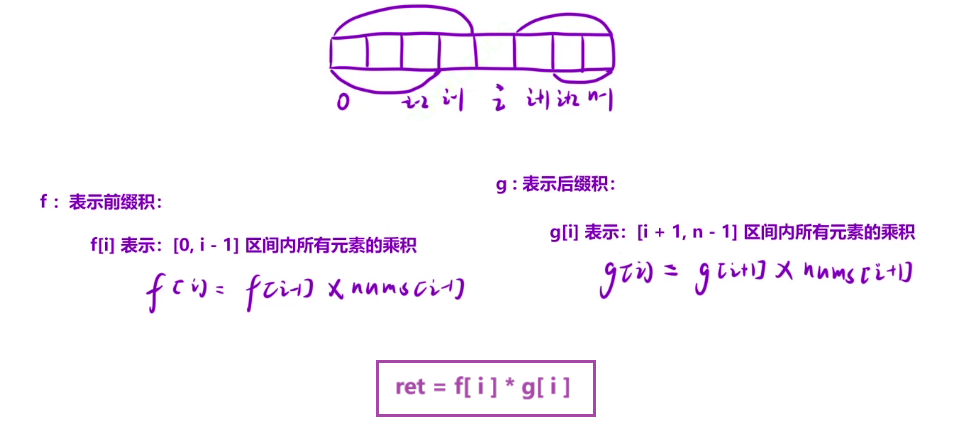
class Solution {
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] f = new int[n];
int[] g = new int[n];
int[] ans = new int[n];
f[0] = 1;
g[n - 1] = 1;
for (int i = 1; i < n; i++) {
f[i] = f[i - 1] * nums[i - 1];
}
for (int i = n - 2; i >= 0; i--) {
g[i] = g[i + 1] * nums[i + 1];
}
for (int i = 0; i < n; i++) {
ans[i] = f[i] * g[i];
}
return ans;
}
}5. 和为 K 的子数组
560. 和为 K 的子数组
思路:每次都求0 ~ i - 1 区间内有多少个子数组是和为 k 的,如果正常求的话,时间复杂度就是O(n^2)了,所以说可以把子数组和为k的个数存在哈希表中去求,也就需要在求和的过程中就把这些数据添加到哈希表中,而求0 ~ i - 1 区间,和为 k 的子数组,就可以转化为求前半部分的哪段区间的和为整段区间和 sum - k
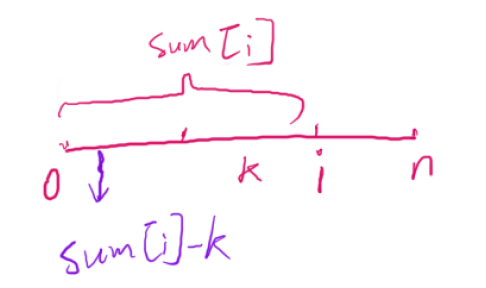
注意点:
- 不用真正的创建一个前缀和数组去表示和,只需要用一个 sum 变量来计算即可
- 如果说整个前缀和都等于k的话,就代表 sum - k 等于 0,这个需要提前在哈希表中存储,因为此时需要在 0~-1 区间内去找一个和为0的次数,但是这个区间不存在,所以说需要提前设置为 1,当需要查找的时候,就是默认的 1
- 前缀和加入到哈希表的时机:需要在计算i位置之前,保存0~i-1区间的前缀和,也就是知道 sum - k的次数,i-1统计之后才可以把i位置的前缀和存入哈希表中
class Solution {
public int subarraySum(int[] nums, int k) {
int sum = 0,ret = 0;
HashMap<Integer,Integer> hash = new HashMap<>();
hash.put(0,1);
for(int x : nums){
sum+=x;
//以当前元素为结尾时有多少符合条件的答案
ret+=hash.getOrDefault(sum - k,0);
hash.put(sum,hash.getOrDefault(sum,0) + 1);
}
return ret;
}
}6. 和可被 K 整除的子数组
974. 和可被 K 整除的子数组

同余定理:(a - b) / p = k......0 => a % p = b % p
就是如果 a - b 的差能够被 p 整除的话,那么 a 和 b 对 p 取模就相等
在 Java 中,一个负数对一个正数取模的话得到的是一个负数,如果想要修正为正数的话可以使用下面的式子

首先把负数的余数变为正数,但如果原来就是正数的话还是不对的,所以需要再取一个余数
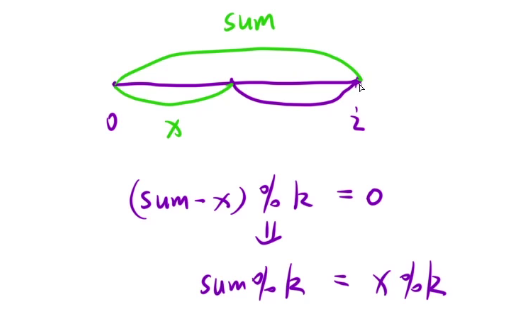
这样就可以把题目转化为只需要求在 i 之前有多少个区间对 K 取模之后等于 0 ,也就和上一题类似了
class Solution {
public int subarraysDivByK(int[] nums, int k) {
int sum = 0, ret = 0;
HashMap<Integer, Integer> hashMap = new HashMap<>();
hashMap.put(0 % k, 1);
for (int x : nums) {
sum += x;
int r = (sum % k + k)% k;
ret += hashMap.getOrDefault( r, 0);
hashMap.put(r, hashMap.getOrDefault(r, 0) + 1);
}
return ret;
}
}7. 连续数组
525. 连续数组

如果直接统计 0 和 1 的个数的话还是比较麻烦的,可以转化一下,把所有的 0 都变成 - 1,当 0 和 1 的个数相等时,也就是区间和等于 0 的情况,也就转化为了之前的求和为 k 的子数组的问题,只不过之前求的是个数,这题求的是长度,
class Solution {
public int findMaxLength(int[] nums) {
HashMap<Integer, Integer> hash = new HashMap<>();
hash.put(0, -1);
int sum = 0, ret = 0;
for (int i = 0; i < nums.length; i++) {
sum += (nums[i] == 0 ? -1 : 1);
if (hash.containsKey(sum)) {
ret = Math.max(ret, i - hash.get(sum));
} else {
hash.put(sum, i);
}
}
return ret;
}
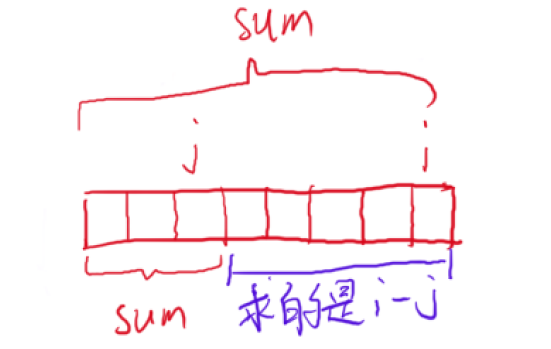
}需要注意的是,如果说在之后发现有重复的 sum 的时候,就不需要再存放进哈希表中了,因为此时的长度肯定是没有第一次的长的,就会影响后面使用 i - j 时计算的长度
8. 矩阵区域和
1314. 矩阵区域和
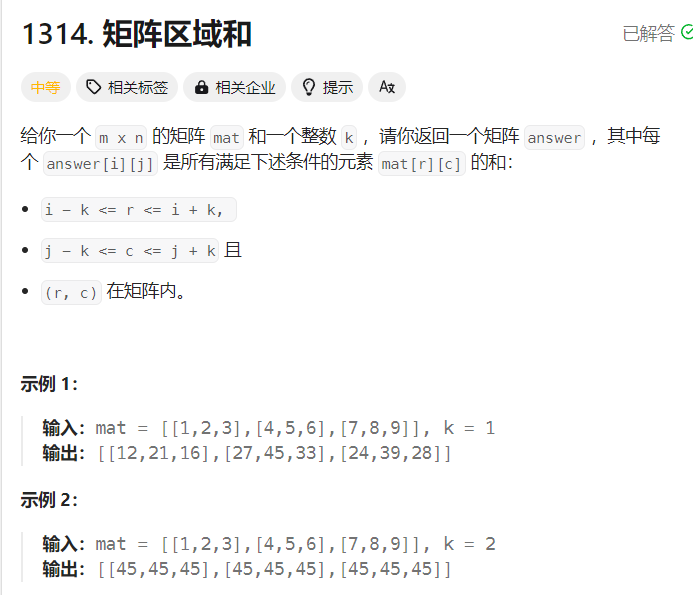
也就是周围所有元素的和
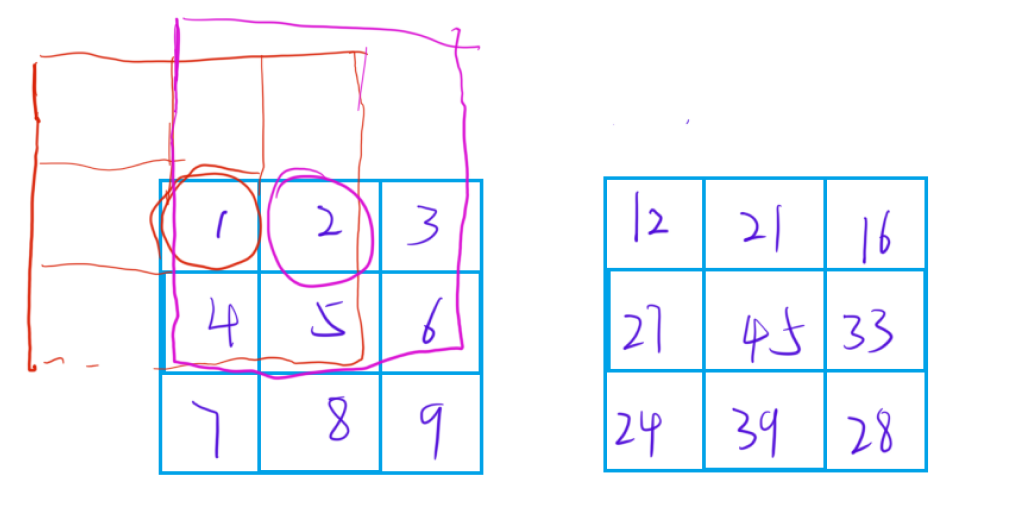
首先就是先预处理一个二维前缀和数组,然后再求( i , j ) 位置的值
求(i , j )位置的值的时候和之前讲的前缀和模版类似
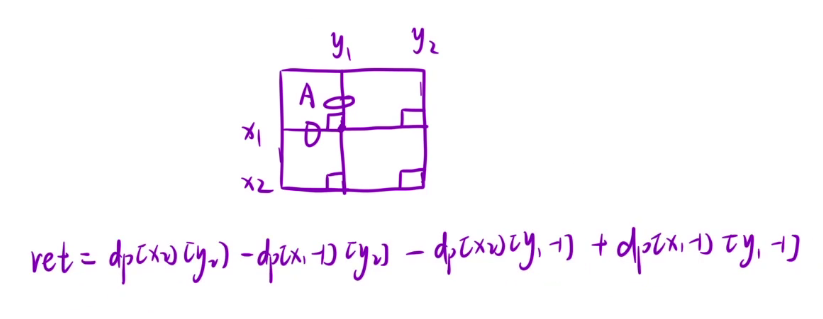
然后就是怎么求坐标的问题,知道(i , j)坐标之后,求此处的值的话就需要求左上角和右下角的坐标,然后才能求出这个区域中的元素和

关于下标的映射关系,由于题目中的数组是从下标 0 计算的,为了方便是将 dp 表从下标为 1 开始计算的,所以说后续再继续从 dp 表中使用值的时候是需要把 x ,y 坐标都加上 1 的
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
int m = mat.length, n = mat[0].length;
int[][] dp = new int[m + 1][n + 1];
int[][] ans = new int[m][n];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j-1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
for(int i = 0; i< m;i++){
for(int j = 0;j < n;j++){
int x1 = Math.max(0,i - k) + 1,y1 = Math.max(0,j - k) + 1;
int x2 = Math.min(m - 1,i + k) + 1,y2 = Math.min(n - 1, j + k) + 1;
ans[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];
}
}
return ans;
}
}











![[uni-app]小兔鲜-06地址+sku+购物车](https://img-blog.csdnimg.cn/img_convert/234f86a989fee0af08e1601374fc44da.png)