12.梯度下降法的具体解析——举足轻重的模型优化算法

news2024/10/4 3:08:47

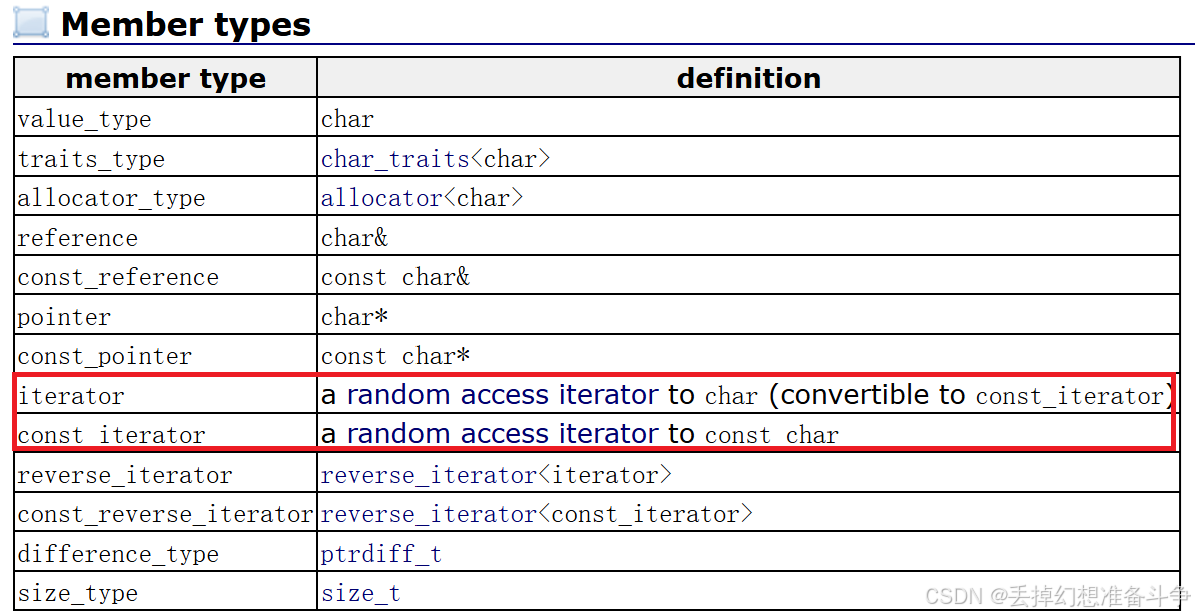
引言

梯度下降法(Gradient Descent)是一种广泛应用于机器学习领域的基本优化算法，它通过迭代地调整模型参数，最小化损失函数以求得到模型最优解。

通过阅读本篇博客，你可以：

1.知晓梯度下降法的具体流程

2.掌握不同梯度下降法的区别

一、梯度下降法的流程

梯度下降法的流程通常分为以下四个步骤。

1.初始化模型参数

初始化模型参数其实就是random随机一个初始的 $\theta$ (一组 $W_{0},...,W_{n}$ )。这样我们就可以得到上图中的 Starting Point(开始点)。

2.计算当下参数的梯度

计算模型参数的梯度，其实就是对于当前损失函数所在位置进行求偏导，公式：

$gradient_{j} = \frac{\partial J(\theta)}{\partial \theta_{j}}$

公式推导 $J(\theta)$ 是损失函数， $\theta_{j}$ 是样本中某个特征维度 $x_{j}$ 对应的权值系数，也可以写成 $W_{j}$ 。对于多元线性回归来说，损失函数 $J(\theta) = \frac{1}{2}(h_{\theta}x - y)^{2}$ (推导过程在9.深入线性回归推导出MSE——不容小觑的线性回归算法-CSDN博客中)，因为我们的MSE中 $X$ 、 $y$ 是已知的， $\theta$ 是未知的，而 $\theta$ 不是一个变量而是许多向量组成的矩阵，所以我们只能对含有一堆变量的函数MSE中的一个变量求导，即偏导，下面就是对 $\theta_{j}$ 求偏导。

$\frac{\partial J(\theta)}{\partial \theta_{j}} = \frac{\partial \frac{1}{2}(h_{\theta}x-y)^{2}}{\partial \theta_{j}}$

由于链式求导法则，我们可以推出：

$\Rightarrow \frac{\partial J(\theta)}{\partial \theta_{j}} = 2 \cdot \frac{1}{2}(h_{\theta}x-y) \cdot\frac{\partial (h_{\theta}x - y)}{\partial \theta_{j}}$

在多元线性回归中， $h_{\theta}x$ 就是 $W^{T}X$ ，也就是 $\omega _{0}x_{0} + \omega_{1}x_{1}+...+\omega_{n}x_{n}$ ，我们通常把它写成 $\sum_{n}^{i = 0}\omega _{i}x_{i}$ ，所以继续推导公式：

$\Rightarrow \frac{\partial J(\theta)}{\partial \theta_{j}} = (h_{\theta}x - y) \cdot \frac{\partial \sum_{n}^{i =0}(\theta_{i}x_{i}-y)}{\partial \theta_{j}}$

由于我们是对 $\theta_{j}$ 求偏导，那么和 $\theta_{j}$ 无关的可以忽略不计，所以公式变为：

$\Rightarrow \frac{\partial J(\theta)}{\partial \theta_{j}} = (h_{\theta}x - y) \cdot x_{j}$

所以，我们可以得到结论： $\theta_{j}$ 对应的梯度(gradient)与预测值 $\hat{y}$ 和真实值 $y$ 有关，同时还与每个特征维度 $x_{j}$ 有关。如果我们分别对每个维度求偏导，即可得到所有维度对应的梯度值。

3.根据梯度和学习率更新参数

通过11.梯度下降法的思想——举足轻重的模型优化算法-CSDN博客的学习，我们已经知道了梯度下降法的公式：

$W_{j}^{t+1} = W_{j}^{t} - \eta \cdot gradient_{j}$

在获得了梯度之后，我们可以将公式表示为：

$W_{j}^{t+1} = W_{j}^{t} - \eta \cdot (h_{\theta}x - y) \cdot x_{j}$

通过这个公式我们就可以去更新参数逼近最优解。

4.判断是否收敛

在如何判断收敛问题上，我相信大多数的人都会认为直接判断梯度(gradient)是否为0。其实这样的方法是错误的，由于非凸损失函数的存在， $gradient = 0$ 的情况可能是极大值！所以我们使用了另外一种方法，设置合理的阈值(Threshold)来界定函数是否收敛。即判断不等式：

$Loss^{t} - Loss^{t+1} < Threshold$

如果前一次的损失函数 $Loss^{t}$ 减去这次迭代后的损失函数 $Loss^{t+1}$ 小于我们设定的阈值 $Threshold$ ，那我们认为函数收敛，当前的参数就是我们寻求的最优解。反之，我们重复第二步与第三步，一直达到最优解为止。其实我们是在判断 $Loss$ 的下降收益是否更合理，随着迭代次数的增多， $Loss$ 减小的幅度不再变化就可以认为停止在最低点。

二、梯度下降法的分类

我们根据梯度下降法流程中求取梯度的步骤样本数量的不同，将梯度下降法分为三个基本的类别。它们每次学习(更新模型参数)使用的样本个数，每次更新使用不同的样本会导致每次学习的准确性和学习时间不同。

1.全量梯度下降(Batch Gradient Descent)

全量梯度下降(Batch Gradient Descent)通过使用整个数据集在每次迭代中计算损失函数的梯度，以此更新模型参数(也称批量梯度下降)。由于我们使用整个数据集的样本，所以全量梯度下降的公式为：

$W_{j}^{t+1} = W_{j}^{t} - \eta \cdot \sum_{m}^{i = 1}(h_{\theta}x_{i} - y_{i}) \cdot x_{j}$

在全量梯度下降中，对于 $\theta$ 的更新，所有的样本都有贡献，也就是参与调整 $\theta$ 。所以从理论上来说一次更新的幅度是比较大的。

全量梯度下降法的优点在于收敛稳定，每次更新都朝着全局最优的方向移动。并且能够净化噪声，由于使用整个数据集计算梯度，随机噪声对更新的影响较小，使得损失函数的路径相对平滑。

缺点也是相当明显，当数据集非常大时，全量梯度下降法每个迭代计算数据集的梯度是非常耗时且占用内存的。所以不适合处理实时数据，比如在线学习和实时更新数据场景。

上图表示的梯度下降法中两个维度参数的关系，我们可以将圆圈看成一个碗的俯视图，碗底就是我们要找的最优解。我们不难发现，全量梯度下降法每次迭代都直接向碗底行进，目标明确。

2.随机梯度下降(Stochastic Gradient Descent)

随机梯度下降(Stochastic Gradient Descent)通过使用数据集中的一个随机样本在每次迭代中计算损失函数的梯度，以此更新模型参数。由于使用随机的一个样本，所以随机梯度下降的公式就是：

$W_{j}^{t+1} = W_{j}^{t} - \eta \cdot (h_{\theta}x - y) \cdot x_{j}$

随机梯度下降的优点在于计算速度快，由于每次迭代只对一个样本计算梯度，因此更新速度快，适合大规模数据集。它还拥有更强的泛化能力，由于引入了随机性，SGD能更好地跳出局部最优，避免过拟合(过拟合相关内容会在专栏后续文章中更新)。并且能够处理实时数据，可以在线学习，所以适用于动态更新的场景。

同样地，由于每次更新只基于一个样本，SGD的收敛并不稳定，梯度波动较大，会导致损失函数的收敛路径不平稳。并且由于随机性的存在，SGD通常需要更多的迭代次数才能收敛到最优解，即收敛速度变慢。

从上图我们可以看出，相比较全量梯度下降，SGD需要迭代更多的次数才能找到最优解。

3.小批量梯度下降(Mini-batch Gradient Descent)

小批量梯度下降(Mini-batch Gradient Descent)通过使用数据集的一部分样本在每次迭代中计算损失函数的梯度，以此更新模型参数。由于使用了数据集的部分样本，所以小批量梯度下降的公式为：

$W_{j}^{t+1} = W_{j}^{t} - \eta \cdot \sum_{batchsize}^{i = 1}(h_{\theta}x_{i} - y_{i}) \cdot x_{j}$

小批量梯度下降综合了全量梯度下降与随机梯度下降，在更新速度与更新次数中取得一个平衡。其每次更新从数据集中随机选择 $batchsize$ 个样本进行学习。相对于随机梯度下降法，小批量梯度下降法降低了收敛的波动性(降低了参数更新的方差)，使得更新更加稳定。相对于全量梯度下降法，其提高了每次学习的速度。