第一题（完全二叉树的最多结点个数）

一棵完全二叉树第六层有9个叶结点（根为第一层），则结点个数最多有（）
A 112
B 111
C 107
D 109

第六层有2^(6-1)，也就是32个结点，其中有9个叶子结点，所以只有23个结点有第七层，也就是说第七层少了9*2个结点
如果七层全满的话，一共有2^7-1=127个结点，减去18个结点，也就是109个结点

D

第二题（哈夫曼树的带权路径长度）

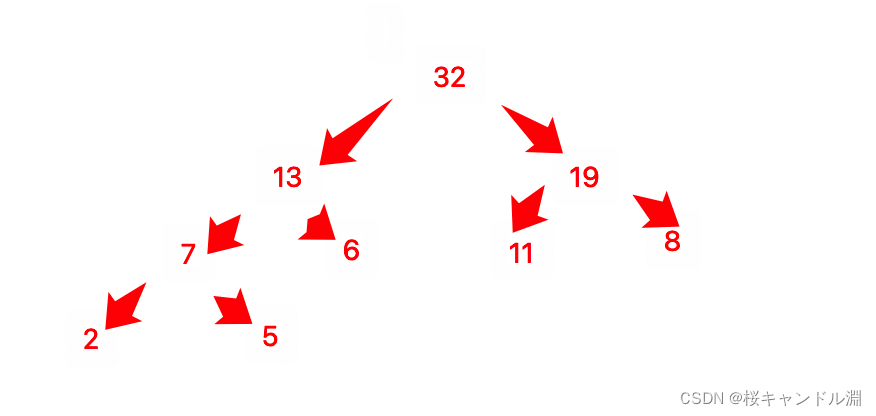
有权值分别为11，8，6，2，5的叶子结点生成一棵哈夫曼树，它的带权路径长度为（）
A 24
B 71
C 48
D 53

也就是2×6+2×11+2×8+3×2+3×5=12+22+16+6+15=71
所以我们带权路径的长度为71

B

第三题（堆的重建）

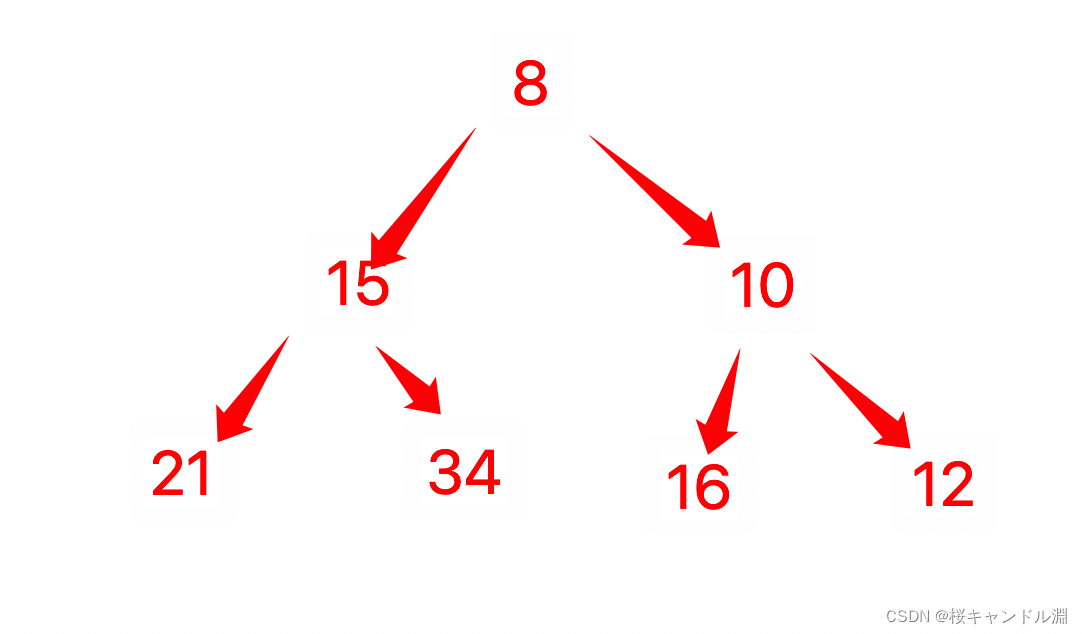
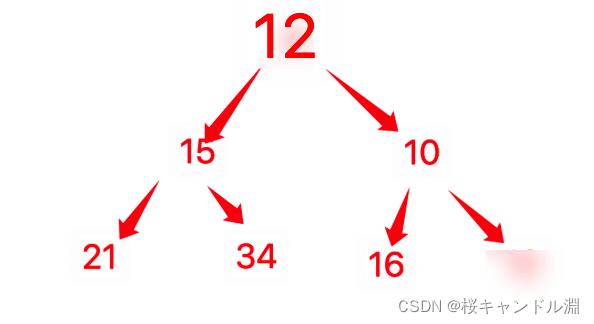
已知小根堆为8,15,10,21,34,16,12，删除关键字8之后需重建堆，最后的叶子节点为（）
A 34
B 21
C 16
D 12

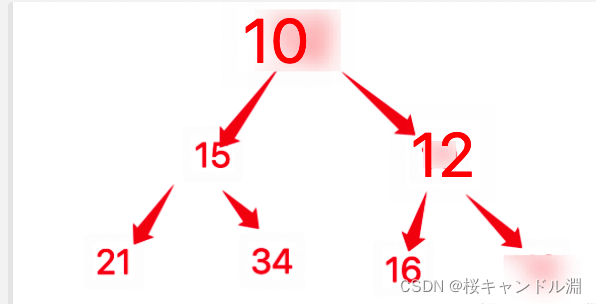
所以我们重建堆之后，我们最后一个元素为16

C

第四题（哈希映射的冲突）

将10个元素散列到100000个单元的哈希表中,则()产生冲突
A 一定会
B 一定不会
C 仍可能会

即使空间很大，数据很小，我们只能说冲突的概率比较小，并不能说明一定能避免哈希冲突。我们依旧有可能两个数的哈希映射值是相同的。

C