K近邻算法 度量距离

欧氏距离(Euclidean distance)

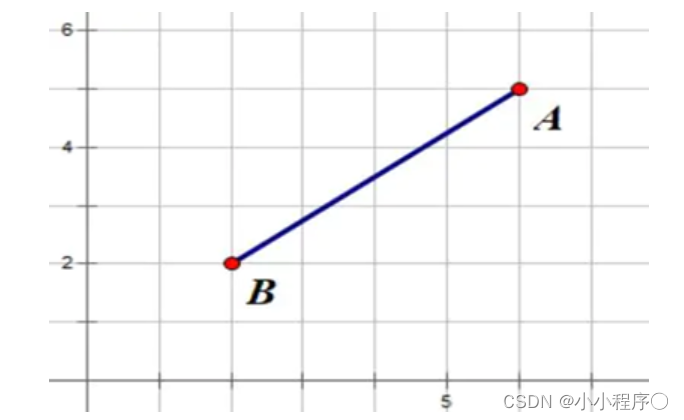
• 欧几里得度量(euclidean metric)(也称欧氏距离)是一个通常采用的距离定义，指在$m$维空间中两个点之间的真实距离，或者向量的自然长度(即该点到原点的距离)。在二维和三维空间中的欧氏距离就是两点之间的实际距离。

距离公式：

$$d\left(x,y\right)=\sqrt{\sum _i(x_i-y_i{)}^2}$$

曼哈顿距离(Manhattan distance)

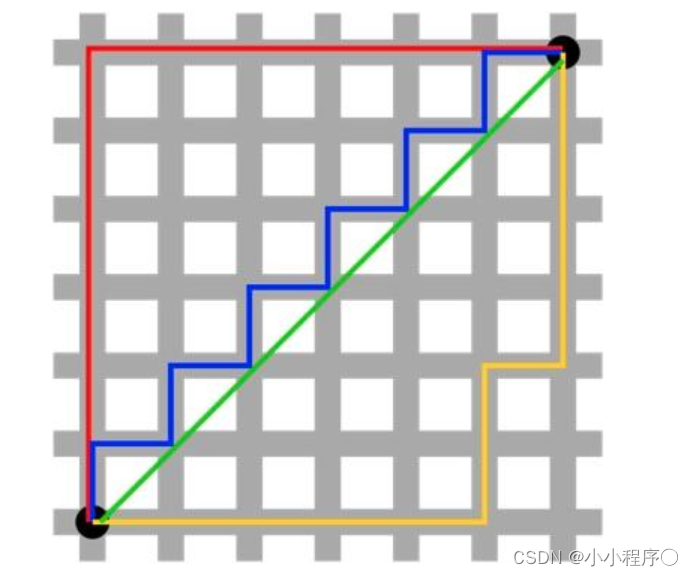
• 想象你在城市道路里，要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源，曼哈顿距离也称为城市街区距离(City Block distance)。

距离公式：

$$d(x,y)=\sum _i|x_i-y_i|$$

切比雪夫距离(Chebyshev distance)

• 在数学中，切比雪夫距离(Chebyshev distance)或是L∞度量，是向量空间中的一种度量，二个点之间的距离定义是其各坐标数值差绝对值的最大值。以数学的观点来看，切比雪夫距离是由一致范数(uniform norm)(或称为上确界范数)所衍生的度量，也是超凸度量(injective metric space)的一种。

距离公式：

$$d\left(x,y\right)=\underset{i}{\max }\left|x_i-y_i\right|$$

若将国际象棋棋盘放在二维直角座标系中，格子的边长定义为1，座标的$x$轴及$y$轴和棋盘方格平行，原点恰落在某一格的中心点，则王从一个位置走到其他位置需要的步数恰为二个位置的切比雪夫距离，因此切比雪夫距离也称为棋盘距离。例如位置F6和位置E2的切比雪夫距离为4。任何一个不在棋盘边缘的位置，和周围八个位置的切比雪夫距离都是1。

闵可夫斯基距离(Minkowski distance)

• 闵氏空间指狭义相对论中由一个时间维和三个空间维组成的时空，为俄裔德国数学家闵可夫斯基(H.Minkowski,1864-1909)最先表述。他的平坦空间(即假设没有重力，曲率为零的空间)的概念以及表示为特殊距离量的几何学是与狭义相对论的要求相一致的。闵可夫斯基空间不同于牛顿力学的平坦空间。$p$取1或2时的闵氏距离是最为常用的，$p=2$即为欧氏距离，而$p=1$时则为曼哈顿距离。

当$p$取无穷时的极限情况下，可以得到切比雪夫距离。
距离公式：

$$d\left(x,y\right)={\left(\sum _i|x_i-y_i{|}^p\right)}^{\frac{1}{p}}$$

汉明距离(Hamming distance)

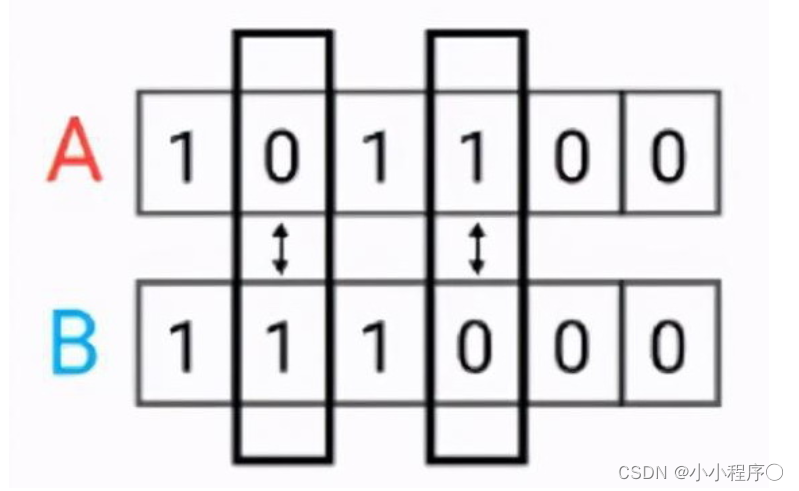
• 汉明距离是使用在数据传输差错控制编码里面的，汉明距离是一个概念，它表示两个(相同长度)字对应位不同的数量，我们以表示两个字,之间的汉明距离。对两个字符串进行异或运算，并统计结果为1的个数，那么这个数就是汉明距离。

距离公式：

$$d\left(x,y\right)=\frac{1}{N}\sum _i{1}_{x_i\ne y_i}$$

余弦相似度(Cosine Similarity)

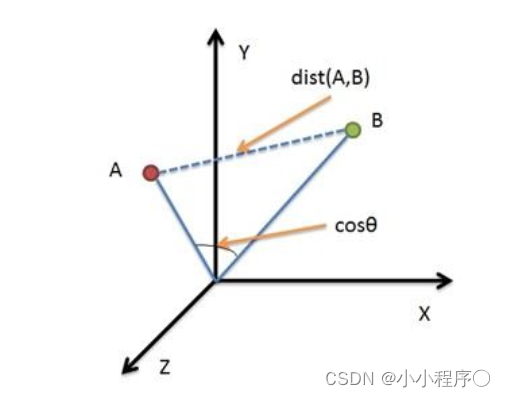
• 余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。
• 0度角的余弦值是1，而其他任何角度的余弦值都不大于1；并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。
• 两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。这结果是与向量的长度无关的，仅仅与向量的指向方向相关。
• 余弦相似度通常用于正空间，因此给出的值为0到1之间。

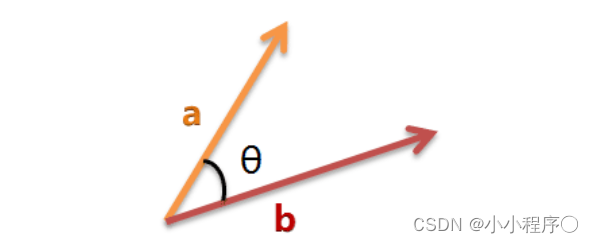
• 二维空间为例，上图的$a$和$b$是两个向量，我们要计算它们的夹角θ。余弦定理告诉我们，可以用下面的公式求得：

$$\cos \theta =\frac{a^2+b^2-c^2}{2ab}$$

• 假定$a$向量是$\left[x_1,y_1\right]$，$b$向量是$\left[x_2,y_2\right]$，两个向量间的余弦值可以通过使用欧几里得点积公式求出：

$$\cos \left(\theta \right)=\frac{A\cdot B}{\parallel A\parallel \parallel B\parallel }=\frac{{\sum }_{i=1}^n{A}_i\times B_i}{\sqrt{{\sum }_{i=1}^n(A_i{)}^2\times \sqrt{{\sum }_{i=1}^n(B_i{)}^2}}}$$

$$\cos \left(\theta \right)=\frac{A\cdot B}{\parallel A\parallel \parallel B\parallel }=\frac{\left(x_1,y_1\right)\cdot \left(x_2,y_2\right)}{\sqrt{x_1^2+y_1^2}\times \sqrt{x_2^2+y_2^2}}=\frac{x_1{x}_2+y_1{y}_2}{\sqrt{x_1^2+y_1^2}\times \sqrt{x_2^2+y_2^2}}$$

• 如果向量$a$和$b$不是二维而是$n$维，上述余弦的计算法仍然正确。假定$A$和$B$是两个$n$维向量，$A$是$\left[A_1,A_2,\dots ,A_n\right]$，$B$是$\left[B_1,B_2,\dots ,B_n\right]$，则$A$与$B$的夹角余弦等于：

$$\cos \left(\theta \right)=\frac{A\cdot B}{\parallel A\parallel \parallel B\parallel }=\frac{{\sum }_{i=1}^n{A}_i\times B_i}{\sqrt{{\sum }_{i=1}^n(A_i{)}^2}\times \sqrt{{\sum }_{i=1}^n(B_i{)}^2}}$$

篇末结尾

感谢您的观看，如果觉得还行，请点赞关注支持一下