摘要
A算法广泛应用于路径规划中,但其生成的路径通常在拐点处呈现不平滑的折线。为了提升路径的平滑性,本文提出了一种基于圆弧的平滑处理方法,用于对A算法产生的路径拐点进行优化。通过在MATLAB中进行仿真验证,该方法能够有效减少路径折线,提高路径的可行性和行驶的平稳性。
理论
A算法通过启发式搜索,寻找从起点到目标点的最优路径。虽然该路径能够避开障碍物,但由于算法的离散性,其拐点处存在较大角度变化。本文采用圆弧平滑算法,通过对A路径中的拐点进行局部圆弧化处理,使路径在拐点处更加顺滑。
平滑处理的关键是确定适合的圆弧半径,并保证圆弧与路径的连续性。设定曲线方程为:
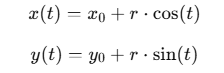
其中, 𝑟为圆弧半径, 𝑥0和 𝑦0为拐点的坐标。
实验结果
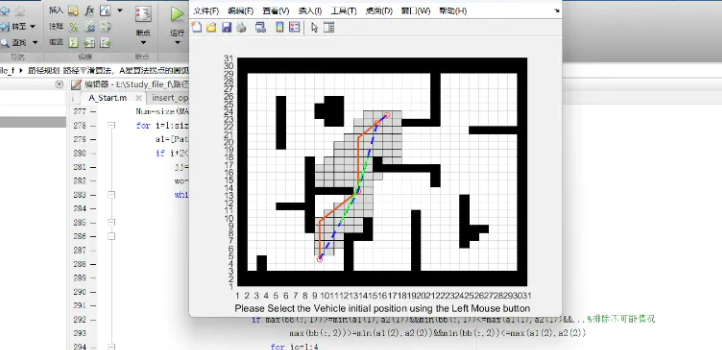
通过MATLAB仿真工具,对A*算法生成的路径进行拐点圆弧化处理,并在不同的地图环境中进行测试。以下为实验结果分析:
图1:基于A*算法的初始路径规划结果,展示了未进行平滑处理的折线路径。 图2:采用圆弧化处理后的路径,路径在拐点处更加平滑。 图3:路径平滑前后的对比,验证了圆弧化处理的有效性。
部分代码
% A*算法路径规划
map = binaryOccupancyMap(30,30); % 创建占用栅格地图
setOccupancy(map,[5 5; 10 10; 15 15],1); % 设置障碍物
startLocation = [2 2];
goalLocation = [28 28];
% 进行A*路径规划
path = plannerAStarGrid(map, startLocation, goalLocation);
% 圆弧平滑处理
smoothedPath = smoothPath(path, 5); % 使用半径为5的圆弧进行平滑
% 绘制路径
figure;
show(map);
hold on;
plot(path(:,1), path(:,2), 'b-', 'DisplayName', 'A*路径');
plot(smoothedPath(:,1), smoothedPath(:,2), 'g-', 'DisplayName', '平滑路径');
legend;
title('基于A*算法的路径平滑处理');
参考文献
❝
Hart, P. E., Nilsson, N. J., & Raphael, B. (1968). A formal basis for the heuristic determination of minimum cost paths. IEEE Transactions on Systems Science and Cybernetics, 4(2), 100-107.
Khatib, O. (1986). Real-time obstacle avoidance for manipulators and mobile robots. The international journal of robotics research, 5(1), 90-98.
Latombe, J. C. (1991). Robot motion planning. Springer Science & Business Media.
Lavalle, S. M. (2006). Planning algorithms. Cambridge university press.