标题:[动态规划] 二叉树中的最大路径和##树形DP#DFS
个人主页@水墨不写bug
(图片来源于网络)
目录
一 、什么是树形DP
二、题目描述(点击题目转跳至题目)
NC6 二叉树中的最大路径和
算法思路:
讲解与参考代码:
正文开始:
// _ooOoo_ //
// o8888888o //
// 88" . "88 //
// (| ^_^ |) //
// O\ = /O //
// ____/`---'\____ //
// .' \\| |// `. //
// / \\||| : |||// \ //
// / _||||| -:- |||||- \ //
// | | \\\ - /// | | //
// | \_| ''\---/'' | | //
// \ .-\__ `-` ___/-. / //
// ___`. .' /--.--\ `. . ___ //
// ."" '< `.___\_<|>_/___.' >'"". //
// | | : `- \`.;`\ _ /`;.`/ - ` : | | //
// \ \ `-. \_ __\ /__ _/ .-` / / //
// ========`-.____`-.___\_____/___.-`____.-'======== //
// `=---=' //
// ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ //
// 佛祖保佑 永无BUG 永不修改 //
一 、什么是树形DP
动态规划(Dynamic Programming)是一种用于解决优化问题的算法思想。它通过将问题分解为子问题,并保存子问题的解,从而避免了重复计算。而树形DP是动态规划的一种具体应用,用于解决树状结构上的问题。
在树形DP中,我们通常会使用深度优先搜索(DFS)的方式来遍历树的节点,并根据遍历的顺序计算每个节点的dp值。
二、题目描述(点击题目转跳至题目)
NC6 二叉树中的最大路径和
二叉树里面的路径被定义为:从该树的任意节点出发,经过父=>子或者子=>父的连接,达到任意节点的序列。
注意:
1.同一个节点在一条二叉树路径里中最多出现一次
2.一条路径至少包含一个节点,且不一定经过根节点
给定一个二叉树的根节点root,请你计算它的最大路径和;
例如:
给出以下的二叉树,
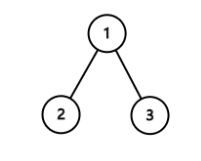
最优路径是:2=>1=>3,或者3=>1=>2,最大路径和=2+1+3=6数据范围:节点数满足 1≤𝑛≤1051≤n≤105 ,节点上的值满足 ∣𝑣𝑎𝑙∣≤1000∣val∣≤1000
要求:空间复杂度 𝑂(1)O(1),时间复杂度 𝑂(𝑛)O(n)
示例1
输入:
{1,2,3}返回值:
6示例2
输入:
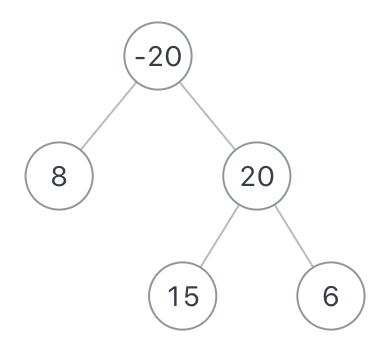
{-20,8,20,#,#,15,6}返回值:
41说明:
其中一条最大路径为:15=>20=>6,路径和为15+20+6=41示例3
输入:
{-2,#,-3}返回值:
-2
算法思路:
树形dp: a. 左子树收集:以左子树为起点的最大单链和; b. 右子树收集:以右子树为起点的最大单链和; c. 根节点要做的事情:整合左右子树的信息,得到经过根节点的最大路径和;d. 向上返回:以根节点为起点的最大单链和
讲解与参考代码:
/** * struct TreeNode { * int val; * struct TreeNode *left; * struct TreeNode *right; * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * }; */ class Solution { public: //树形dp,dfs //找到左(右)子树为根的最大链和 //由于val的返回的绝对值小于1000,所以将ret初始化为负无穷小,在这里-1001即可满足条件 int ret = -1001; int dfs(TreeNode* root) { if(root == nullptr) return 0; //细节:如果子树的最大路径和小于0,则直接返回0即可,不再向上返回 int l = max(0,dfs(root->left)); int r = max(0,dfs(root->right)); ret = max(ret,root->val + l + r); return root->val + max(l,r); } int maxPathSum(TreeNode* root) { dfs(root); return ret; } };
完~
未经作者同意禁止转载