题意

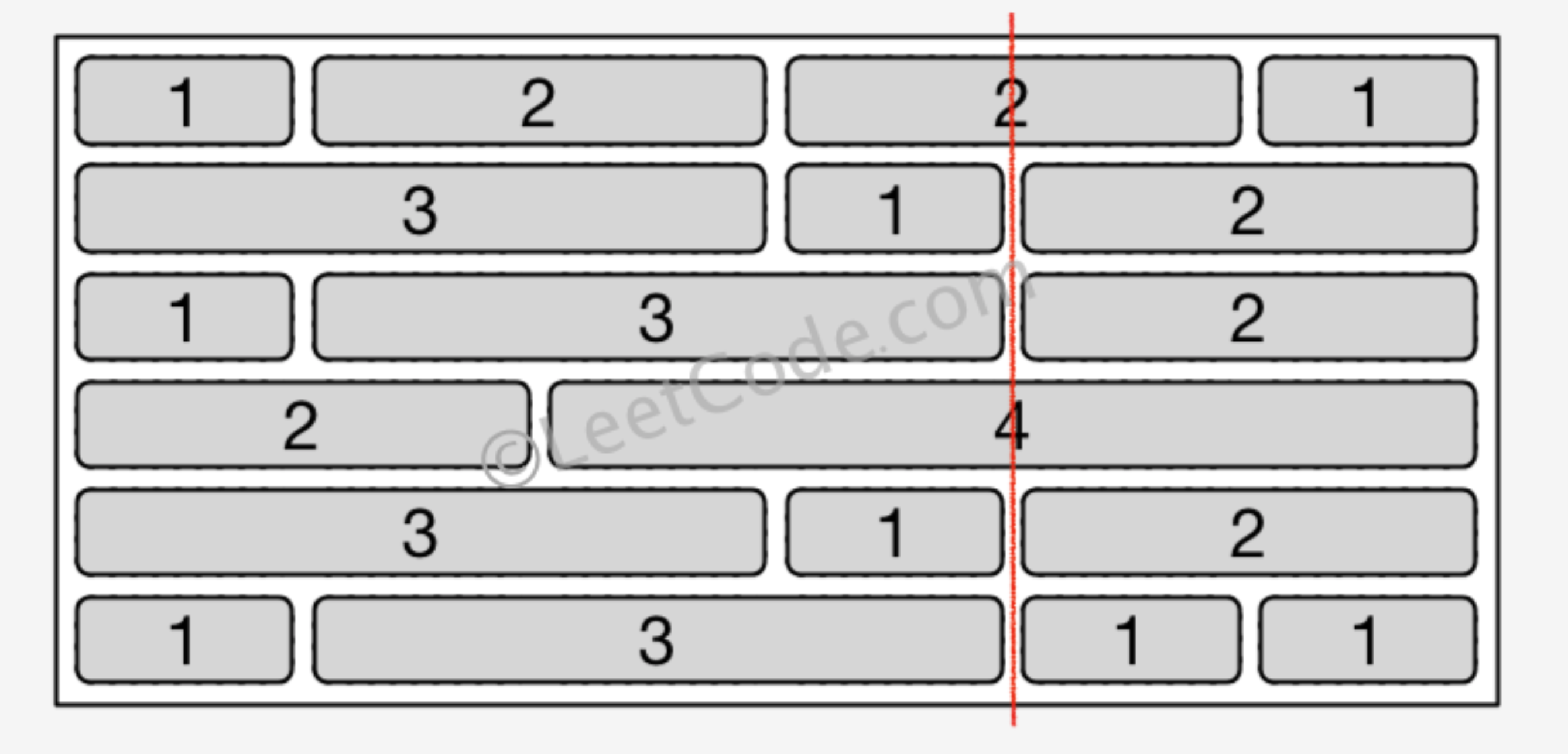
给一个双端队列，双方轮流取数，每一次能且只能从队头或队尾取数，取完数后将这个数从队列中弹出。双方都希望自己取的所有数之和尽量大，且双方都以最优策略行动，假设先手取的所有数之和为 $X$，后手取的所有数之和为 $Y$，求 $X-Y$。

$1\le N\le 3000,1\le a_i\le 10^9$

思路

考虑反向区间dp，记 $d{p}_{l,r}$ 表示剩下 $[l,r]$ 未消除时，消除从 $[l,r]$ 对答案的贡献。

显而易见，对于长度为 $i$ 的区间 $[l,r]$，如果 $cnt-i$ 为奇数，则代表当前是对方取数，否则当前为己方取数。

对于对方取数时，有 $d{p}_{l,r}=\min (d{p}_{l,r-1}-a_r,d{p}_{l+1,r}-a_l)$

对于己方取数时，有 $d{p}_{l,r}=\max (d{p}_{l,r-1}+a_r,d{p}_{l+1,r}+a_l)$

容易发现答案为 $d{p}_{1,n}$。

代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,dp[3005][3005],a[3005];
int ans;

signed main() {
	scanf("%lld",&n);
	for(int i = 1;i <= n;i++) scanf("%lld",&a[i]);
	for(int i = 1;i <= n;i++) {
		for(int l = 1;l + i - 1 <= n;l++) {
			int r = l + i - 1;
			if((n - i) & 1) {
				dp[l][r] = min(dp[l][r - 1] - a[r],dp[l + 1][r] - a[l]);
			}
			else dp[l][r] = max(dp[l][r - 1] + a[r],dp[l + 1][r] + a[l]);
			//printf("(%lld,%lld)%lld\n",l,r,dp[l][r]);
		}
	}
	printf("%lld\n",dp[1][n]);
}