文章目录
- 1. 归并排序简介
- 1.1 归并排序定义
- 1.2 归并排序特点
- 2. 归并排序步骤过程拆解
- 2.1 分割数组
- 2.2 递归排序
- 2.3 合并有序数组
- 3. 归并排序的优化
- 3.1 原地归并排序
- 3.2 混合插入排序
- 案例代码和动态图
- 4. 归并排序的优点
- 5. 归并排序的缺点
- 总结

【 已更新完 TypeScript 设计模式 专栏,感兴趣可以关注一下,一起学习交流🔥🔥🔥 】
1. 归并排序简介
1.1 归并排序定义
归并排序是一种高效的、基于比较的排序算法,它的核心思想是"分而治之"。假设你是一个厨师,需要制作一大锅复杂的汤。你采用这样的策略:首先将食材分成两组,放在两个锅里,你继续将每个锅里的食材再分成两份,直到每个小锅里只有一种食材。你开始两两比较相邻小锅里的食材,将它们按照口味搭配合并到一个新的锅中,不断重复这个过程,直到所有的食材都被合并到一个完美调和的大锅汤里。这就是归并排序的基本思想。
用TypeScript代码表示一个简单的归并排序:
function mergeSort(arr: number[]): number[] {
if (arr.length <= 1) return arr;
const mid = Math.floor(arr.length / 2);
const left = arr.slice(0, mid);
const right = arr.slice(mid);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left: number[], right: number[]): number[] {
let result: number[] = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
return result.concat(left.slice(leftIndex)).concat(right.slice(rightIndex));
}
1.2 归并排序特点
- 分治思想: 归并排序采用分治策略,将复杂问题分解为简单子问题
- 稳定性: 归并排序是稳定的排序算法
- 时间复杂度: 无论最好、最坏还是平均情况,时间复杂度都是O(nlogn)
- 空间复杂度: 需要额外的O(n)空间
2. 归并排序步骤过程拆解
2.1 分割数组
const mid = Math.floor(arr.length / 2);
const left = arr.slice(0, mid);
const right = arr.slice(mid);
如厨师将一大堆食材分成两份,他们不断地分割,直到每个小碗里只剩下一种食材。
2.2 递归排序
return merge(mergeSort(left), mergeSort(right));
这个步骤就像每个厨师都在独立地整理自己那一小堆食材,只有一种食材时,它自然就是有序的。
2.3 合并有序数组
function merge(left: number[], right: number[]): number[] {
let result: number[] = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
return result.concat(left.slice(leftIndex)).concat(right.slice(rightIndex));
}
这个步骤就像两位厨师比较各自盘子里最小的食材,将较小的那个放到新的大盘子中,不断重复这个过程,直到所有的食材都合并到新的大盘子中,形成一道完整的菜肴。
3. 归并排序的优化
3.1 原地归并排序
function inPlaceMergeSort(arr: number[], start: number = 0, end: number = arr.length - 1): void {
if (start >= end) return;
const mid = Math.floor((start + end) / 2);
inPlaceMergeSort(arr, start, mid);
inPlaceMergeSort(arr, mid + 1, end);
inPlaceMerge(arr, start, mid, end);
}
function inPlaceMerge(arr: number[], start: number, mid: number, end: number): void {
let left = start;
let right = mid + 1;
let temp: number[] = [];
while (left <= mid && right <= end) {
if (arr[left] <= arr[right]) {
temp.push(arr[left]);
left++;
} else {
temp.push(arr[right]);
right++;
}
}
while (left <= mid) {
temp.push(arr[left]);
left++;
}
while (right <= end) {
temp.push(arr[right]);
right++;
}
for (let i = 0; i < temp.length; i++) {
arr[start + i] = temp[i];
}
}
就像厨师在制作汤时,不是每次都拿出新的锅来装食材,而是直接在原来的大锅里进行操作。这样可以节省一些厨具空间,可能会稍微增加一些烹饪时间。
3.2 混合插入排序
function hybridMergeSort(arr: number[], threshold: number = 10): number[] {
if (arr.length <= threshold) {
return insertionSort(arr);
}
const mid = Math.floor(arr.length / 2);
const left = arr.slice(0, mid);
const right = arr.slice(mid);
return merge(hybridMergeSort(left, threshold), hybridMergeSort(right, threshold));
}
function insertionSort(arr: number[]): number[] {
for (let i = 1; i < arr.length; i++) {
let current = arr[i];
let j = i - 1;
while (j >= 0 && arr[j] > current) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = current;
}
return arr;
}
这个优化版本就像厨师在制作汤时,发现食材数量少于某个阈值(比如10种)时,直接用更简单的烹饪方法,这样可以减少复杂的烹饪步骤,提高整体的烹饪效率。
案例代码和动态图
const array = [38, 27, 43, 3, 9, 50, 10];
const sortedArray = mergeSort(array);
console.log(sortedArray); // [3, 9, 10, 27, 38, 43, 50]
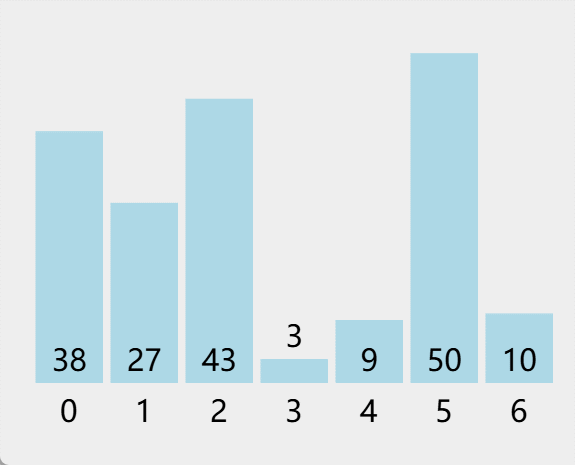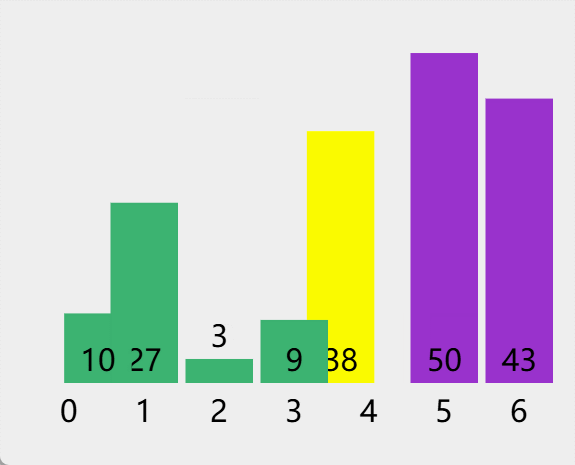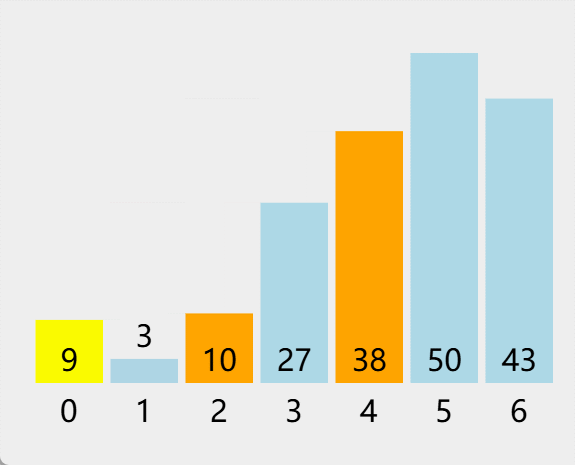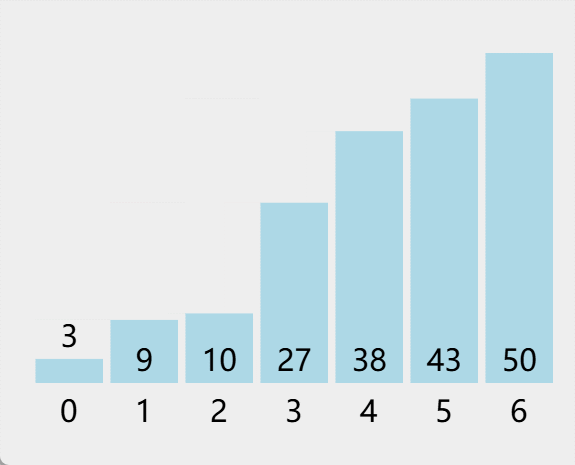
4. 归并排序的优点
- 稳定性好: 归并排序是稳定的排序算法
- 时间复杂度稳定: 无论最好、最坏还是平均情况,时间复杂度都是O(nlogn)
- 适合外部排序: 当数据量很大,无法一次性加载到内存时,归并排序特别有用
5. 归并排序的缺点
- 空间复杂度高: 需要额外的O(n)空间
- 对于小规模数据,不如插入排序等简单算法效率高
总结
归并排序就像是一个团队合作的游戏。面对复杂的问题,先将其分解成小问题,各自解决后再合并结果。这种"分而治之"的思想不仅在排序算法中有用,在我们日常解决问题时也常常能派上用场。
归并排序的稳定性和时间复杂度的优势,使它在处理大规模数据时表现出色。特别是在外部排序中,当数据量大到无法一次性加载到内存时,归并排序的思想就显得尤为重要。
没有一种算法是完美的,归并排序的空间复杂度相对较高,在某些内存受限的场景中可能成为一个问题,对于小规模数据,它不如一些更简单的算法高效。因此了解每种算法的特点和适用场景,在实际应用中做出最佳选择。
喜欢的话就点个赞 ❤️,关注一下吧,有问题也欢迎讨论指教。感谢大家!!!
下期预告: TypeScript 算法手册 - 快速排序