1. 声明和绑定数据
wxml文件
<view> {{school}} </view>
<view>{{obj.name}}</view>
<view id="{{id}}" > 绑定属性值 </view>
<checkbox checked="{{isChecked}}"/>
<!--算数运算-->
<view>{{ id + 1 }}</view>
<!--三元运算-->
<view>{{id===1 ? "等于":"不等于"}}</view>
<!--逻辑判断-->
<view>{{id===1}}</view>
<!--注意:在{{}}语法中,只能写表达式,不能写语句和调用JS方法-->
JS文件
Page({
data: {
school: "西安交通大学",
obj: {
name: "wwww"
},
id: 12,
isChecked: true
},
})

2. setData()修改数据
在小程序中修改数据不推荐使用赋值的方式进行修改,因为无法改变页面的数据。正确的方式应该是通过调用setData()方法来进行修改。

3. setData()修改对象类型的数据
3.1 属性新增
<view> {{userinfo.id}} </view>
<view> {{userinfo.name}} </view>
<button bind:tap="updateUserInfo">修改数据</button>
// pages/test/test.js
Page({
data: {
userinfo:{
}
},
updateUserInfo(){
console.log(this.data.userinfo);
//新增单个/多个属性
this.setData({
'userinfo.name':'tom',
'userinfo.id':1,
})
}
})

3.2 属性值的修改
// pages/test/test.js
Page({
data: {
userinfo:{
name:'',
id:''
}
},
updateUserInfo(){
this.setData({
'userinfo.name':'tom',
'userinfo.id':1,
})
}
})
3.3 实现多属性操作
采用ES6展开运算符方式处理
// pages/test/test.js
Page({
data: {
userinfo:{
name:'',
id:''
}
},
updateUserInfo(){
//复制this.data.userinfo的值到userinfo
//后面加的字段会自动覆盖前面对象里面的属性值
const userinfo ={
... this.data.userinfo,
name:"jerry",
id:18
}
this.setData({
//将上面的userinfothis.data.userinfo
//赋值到键和值如果一样的话,可以简写如下
userinfo
})
}
})

采用Object.assign()方式处理
Object.assign()将多个对象合并成一个对象,从后往前合并,以后面的为准。
// pages/test/test.js
Page({
data: {
userinfo:{
name:'',
id:''
}
},
updateUserInfo(){
const userinfo = Object.assign(this.data.userinfo,{name:'jerry'},{id:18})
this.setData({
//将上面的userinfothis.data.userinfo
//赋值到键和值如果一样的话,可以简写如下
userinfo
})
}
})
3.4 删除单个属性
// pages/test/test.js
Page({
data: {
userinfo: {
name: 'tom',
id: '1'
}
},
updateUserInfo() {
delete this.data.userinfo.id
this.setData({
userinfo: this.data.userinfo
})
}
})

3.5 删除多个属性
// pages/test/test.js
Page({
data: {
userinfo: {
name: 'tom',
id: '1'
}
},
updateUserInfo() {
//删除多个属性 rest 剩余参数
//将userinfo解构到name,id,rest中,也就是rest里面没有name,id,再将其赋给userinfo,自然没有name,id
const {name,id,...rest} = this.data.userinfo
this.setData({
userinfo: rest
})
}
})

4. setData()修改数组数据
4.1 新增数组元素
<view wx:for="{{list}}" wx:key="index" > {{item}} </view>
<button bind:tap="updateList">修改数据</button>
// pages/test/test.js
Page({
data: {
list:[1,2,3,4,5]
},
updateList() {
//新增数组元素,不能直接使用push方法,因为不能更新页面数据,必须要结合setData方法
this.data.list.push(10)
this.setData({
list: this.data.list
})
}
})

// pages/test/test.js
Page({
data: {
list:[1,2,3,4,5]
},
updateList() {
//方式1:新增数组元素,不能直接使用push方法,因为不能更新页面数据,必须要结合setData方法
// this.data.list.push(10)
//方式2: 利用concat方法
const newlist = this.data.list.concat(10);
this.setData({
list: newlist
})
}
})

// pages/test/test.js
Page({
data: {
list:[1,2,3,4,5]
},
updateList() {
//方式1:新增数组元素,不能直接使用push方法,因为不能更新页面数据,必须要结合setData方法
// this.data.list.push(10)
//方式2: 利用concat方法
// const newlist = this.data.list.concat(10);
//方式3:利用ES6的展开运算符
const newlist = [...this.data.list,10]
this.setData({
list: newlist
})
}
})

4.2 修改数组元素
<view> {{list[0].name}} </view>
<button bind:tap="updateList">修改数据</button>
// pages/test/test.js
Page({
data: {
list:[{'name':'tom','age':17}]
},
updateList() {
this.setData({
'list[0].name': 'wuk'
})
}
})

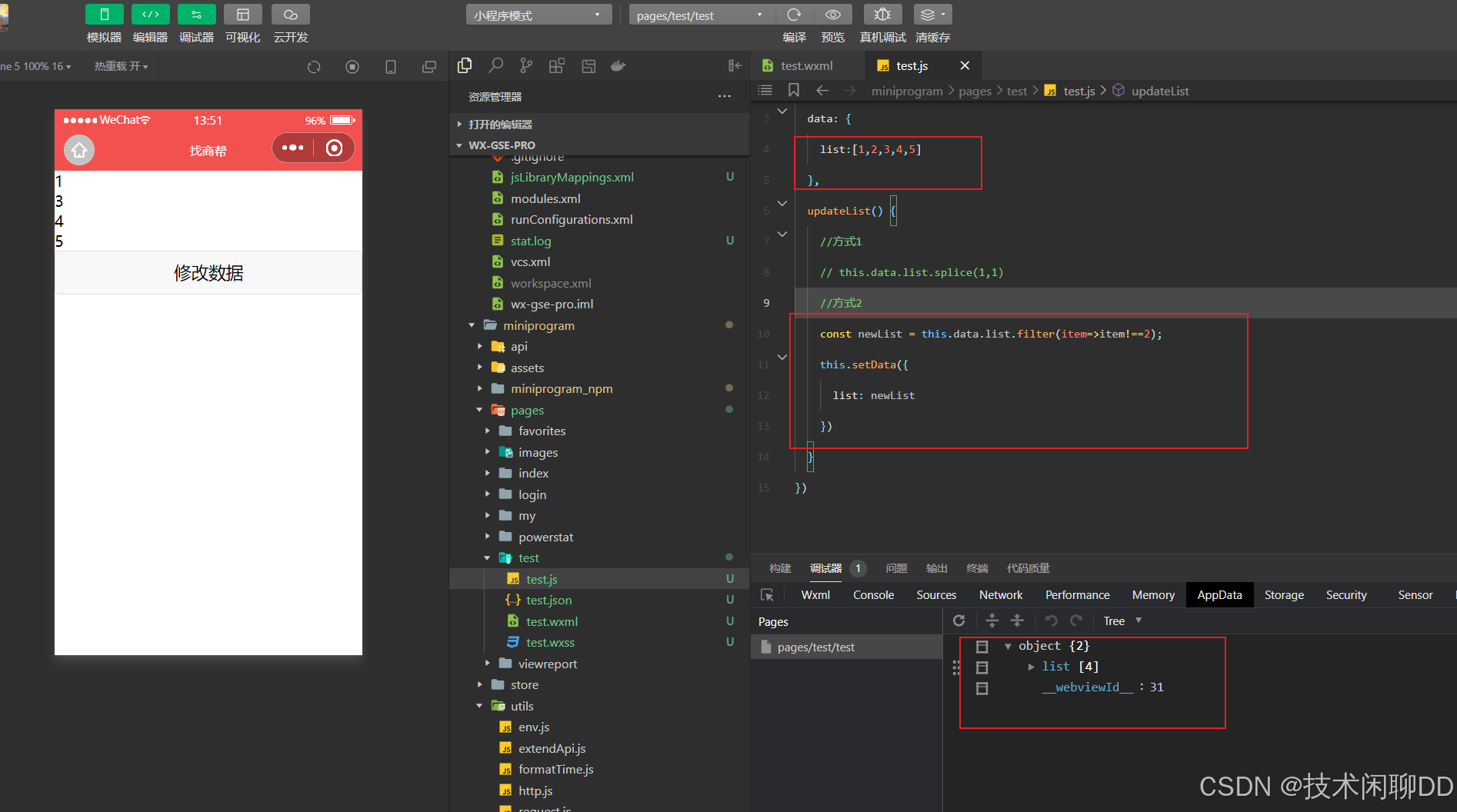
4.3 数组元素删除
<view wx:for="{{list}}" wx:key="index" > {{item}} </view>
<button bind:tap="updateList">修改数据</button>
// pages/test/test.js
Page({
data: {
list:[1,2,3,4,5]
},
updateList() {
//方式1
this.data.list.splice(1,1)
this.setData({
list: this.data.list
})
}
})

// pages/test/test.js
Page({
data: {
list:[1,2,3,4,5]
},
updateList() {
//方式1
// this.data.list.splice(1,1)
//方式2
const newList = this.data.list.filter(item=>item!==2);
this.setData({
list: newList
})
}
})