大家好，这里是效率办公指南！

📐 在数学和工程问题中，线性方程是一类非常基础且常见的问题。无论是解决简单的一元一次方程，还是复杂的多元线性方程组，都有一定的方法和步骤可以遵循。今天，我们将介绍解线性方程的基本方法和步骤，并通过例题示例来加深理解。

解线性方程的方法

1. 代入法

代入法是通过将一个方程的解表示为另一个变量的函数，然后代入到其他方程中求解的方法。

2. 消元法

消元法是通过加减方程以消除一个变量，从而简化方程组的方法。

3. 矩阵方法

矩阵方法涉及到将方程组写成矩阵形式，然后使用矩阵运算（如求逆、秩等）来求解。

解线性方程的步骤

步骤一：整理方程

将方程整理成标准形式，即 ax + by = c。

步骤二：选择方法

根据方程组的特点选择合适的解法。

步骤三：求解

按照选定的方法进行计算，求解方程或方程组。

步骤四：检验

求解完成后，将解代入原方程检验是否正确。

例题示例

示例一：一元一次方程

方程：2x + 3 = 11

解法：

1. 减去3：2x = 8

2. 除以2：x = 4

答案：x = 4

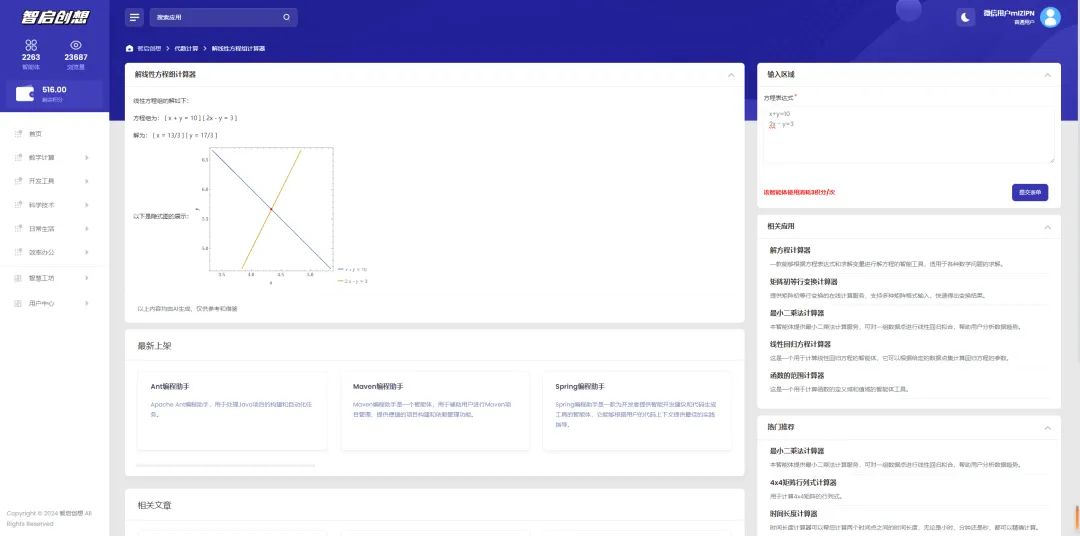
示例二：二元一次方程组

方程组：

x+y=10

2x - y=3

答案： [ x = 13/3 ] [ y = 17/3 ]

总结

掌握解线性方程的方法和步骤对于解决数学和工程问题至关重要。无论是代入法、消元法还是矩阵方法，都能帮助我们找到方程的解。通过上述例题示例，我们可以看到不同方法的应用。如果你有任何疑问或需要进一步的帮助，欢迎在下方留言，我们会尽快为你解答。

微信搜一搜【智启创想】，使用解线性方程计算器