题目链接:

D - Hidden Weights (atcoder.jp)

题目描述:

数据范围限制:

样例:

输入:

3 3
1 2 2
3 2 3
1 3 -1 

输出:

 3 5 2

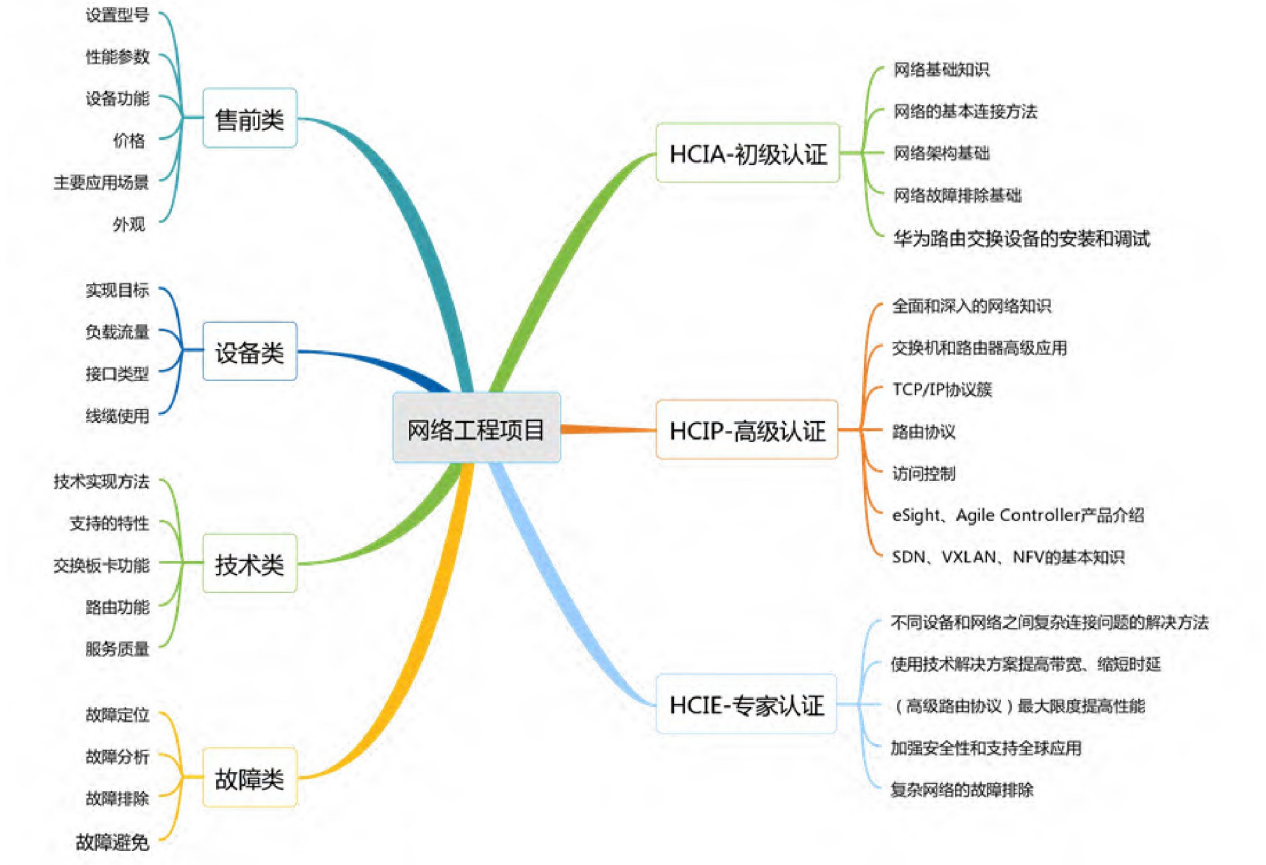
样例图：

 

思路：

 第一次想的是从没有入节点的点去出发，然后去依次去更新，但是发现这个是错误的。

用dfs去暴力搜索，也就是去遍历点。遍历过的点就标记为true，遍历到当前这个点的时候，这个点的后面的点也就会遍历，因此没有必要去重复标记。

注意：在加入点的时候 add(x, y, z) 和 add(y, x, -z) 因为 x到y的距离是z，那么反过来就是-z。为什么要加第二个add呢？要是不加的话dfs() 的时候标记为true,那么后面再去由其他的点遍历到当前这个点的时候，发现为true就不能再去更新了。例如下面这张图，要是不去add(y, x, -z) 的话， 那么在for(int i = 1; i <= n; i ++ ) i=1的时候发现ok[1] = false 然后去dfs,把其标记为true, 然后for的时候发现它没有指向别的边，当遍历到2的时候，发现2的下面有个1，尝试着去更新1的时候，发现1已经被标记为true了，怎么去更新？要是加入add(y, x, -z) 的话就相当于是个双向图了，但是权值是相反的，不过也没事，每个点遵循的原则是：只去更新一次。

这个add两次的这个方法在之前是见过的，但是没想到，我用的是类似与bfs的方法，但是这样是会发生冲突的，用dfs这个不撞南墙不回头的精神，因为答案必存在，那么任何一个起点都是可以的，不会发生冲突。

代码:

#include<bits/stdc++.h>
#define int long long
#define fi first
#define se second
 
using namespace std;

const int N = 2e5 + 10;

vector<pair<int, int> > v[N];
int n, m;
int ret[N];
int ok[N];

// 这样确实会一个点去遍历一次 
void dfs(int x) {
	cout << "x = " << x << endl ;
	ok[x] = true;
	for(auto i : v[x]) {
		//cout << "i = " << i.fi << endl;
		if(!ok[i.fi]) { // 还没有被更新 
			ret[i.fi] = ret[x] + i.se;
		//	cout << "i.fi = " << i.fi << endl;
			dfs(i.fi);;
		}
	}
}

signed main() {
	cin >> n >> m;
	for(int i = 1; i <= m; i ++ ) {
		int x, y, z;
		cin >> x >> y >> z;
		v[x].push_back({y, z});
		v[y].push_back({x, -z}); // 这个是必须要写的
		// 解决了先后的问题 
	}
	
	for(int i = 1; i <= n; i ++ ) {
		if(!ok[i])
		dfs(i);
	}
	
	for(int i = 1; i <= n; i ++ ) {
		cout << ret[i] << " ";
	}
	
	return 0;
}

运行结果: