
引言
大家好,我是GISer Liu😁,一名热爱AI技术的GIS开发者。本系列文章是我跟随DataWhale 2024年9月学习赛的LeetCode学习总结文档;本文主要讲解
位运算算法。💕💕😊
一、 位运算简介
1.什么是位运算?
① 位运算的定义
位运算(Bit Operation)是指直接对整数的二进制位进行操作的运算。在计算机内部,所有的数据都是以二进制形式存储的,因此位运算可以直接操作这些二进制位,从而实现一些高效的计算。
② 优势:提高程序性能
位运算的优势在于其高效性。由于位运算是直接对二进制位进行操作,不需要进行复杂的数值转换,因此在某些情况下,使用位运算可以显著提高程序的性能。例如,在处理大量数据或需要频繁进行位操作的场景中,位运算可以大大减少计算时间。
2.二进制数的基本概念
① 二进制数的表示方法

二进制数(Binary)是由 0 和 1 两个数码组成的数。在计算机中,所有的数据最终都会被转换为二进制形式进行存储和处理。
② 二进制数的位(Bit)
在二进制数中,每一个 0 或 1 被称为一个位(Bit)。位是二进制数的最小单位,多个位组合在一起可以表示更大的数值。
① 二进制与十进制的区别
- 十进制:由
0到9共 10 个数码组成,进位规则是“满十进一”。例如,7 + 2 = 9,9 + 2 = 11。 - 二进制:由
0和1两个数码组成,进位规则是“逢二进一”。例如,1 + 0 = 1,1 + 1 = 10。
② 二进制的进位规则:逢二进一
在二进制中,当某一位的数值达到 2 时,就会向高位进一。例如:
1 + 0 = 11 + 1 = 10(相当于十进制的2)10 + 1 = 11(相当于十进制的3)
③ 示例:二进制数的加法
让我们通过一个简单的例子来理解二进制数的加法:
101 (二进制)
+ 011 (二进制)
------
1000 (二进制)
在这个例子中:
- 最低位
1 + 1 = 10,结果是0,进位1。 - 第二位
0 + 1 + 进位 1 = 10,结果是0,进位1。 - 第三位
1 + 0 + 进位 1 = 10,结果是0,进位1。 - 最高位只有进位
1,结果是1。
最终结果是 1000,即十进制的 8。
3. 二进制数的转换
① 二进制转十进制
转换方法:按权展开
将二进制数转换为十进制数的方法是按权展开。每一位的权值是 2 的幂次方,从右到左依次为 2^0, 2^1, 2^2, …。
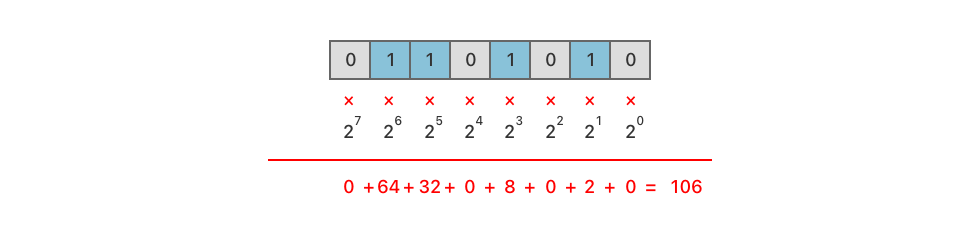
示例:二进制数 01101010 转换为十进制
二进制数:01101010
按权展开:
0 * 2^7 + 1 * 2^6 + 1 * 2^5 + 0 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0
= 0 + 64 + 32 + 0 + 8 + 0 + 2 + 0
= 106
所以,二进制数 01101010 转换为十进制数是 106。
② 十进制转二进制
转换方法:除二取余,逆序排列
将十进制数转换为二进制数的方法是“除二取余,逆序排列”。具体步骤如下:
- 将十进制数不断除以
2,记录每次的余数。 - 将所有余数逆序排列,得到二进制数。
示例:十进制数 106 转换为二进制
106 ÷ 2 = 53 余 0
53 ÷ 2 = 26 余 1
26 ÷ 2 = 13 余 0
13 ÷ 2 = 6 余 1
6 ÷ 2 = 3 余 0
3 ÷ 2 = 1 余 1
1 ÷ 2 = 0 余 1
将余数逆序排列,得到 1101010。由于二进制数通常从高位开始,所以最终结果是 01101010。
所以,十进制数 106 转换为二进制数是 01101010。
通过这些步骤,我们可以理解位运算的基本概念和二进制数的转换方法。接下来,我们将深入探讨位运算的具体操作。
二、位运算基础操作
1.按位与运算(AND)
① 运算符:&
按位与运算使用符号 & 表示。它是一种双目运算符,即需要两个操作数。
② 运算规则
按位与运算的规则是:只有当两个二进位都为 1 时,结果位才为 1。否则,结果位为 0。
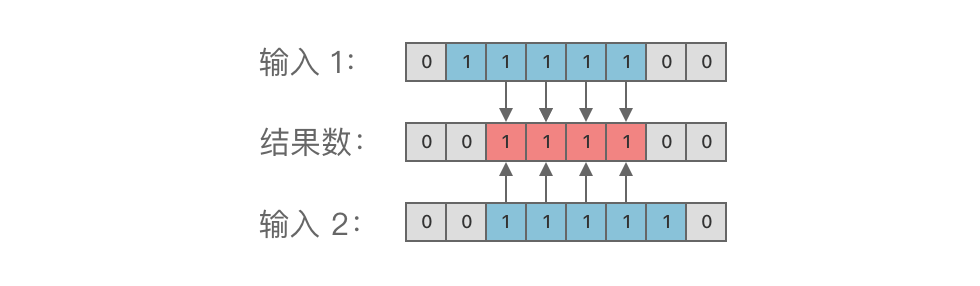
具体规则如下:
1 & 1 = 11 & 0 = 00 & 1 = 00 & 0 = 0
③ 示例
让我们通过一个具体的例子来理解按位与运算:
01111100
& 00111110
----------
00111100
逐位进行与运算:
- 第 1 位:
0 & 0 = 0 - 第 2 位:
0 & 1 = 0 - 第 3 位:
1 & 1 = 1 - 第 4 位:
1 & 1 = 1 - 第 5 位:
1 & 1 = 1 - 第 6 位:
1 & 1 = 1 - 第 7 位:
1 & 1 = 1 - 第 8 位:
0 & 0 = 0
最终结果是 00111100。
2. 按位或运算(OR)
① 运算符:|
按位或运算使用符号 | 表示。它也是一种双目运算符,需要两个操作数。
② 运算规则
按位或运算的规则是:只要有一个二进位为 1,结果位就为 1。否则,结果位为 0。
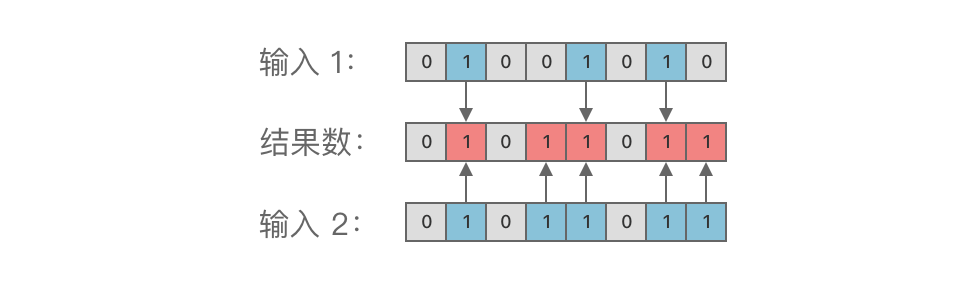
具体规则如下:
1 | 1 = 11 | 0 = 10 | 1 = 10 | 0 = 0
③ 示例:
下面通过一个具体的例子来理解按位或运算:
01001010
| 01011011
----------
01011011
逐位进行或运算:
- 第 1 位:
0 | 1 = 1 - 第 2 位:
1 | 1 = 1 - 第 3 位:
0 | 0 = 0 - 第 4 位:
0 | 1 = 1 - 第 5 位:
1 | 1 = 1 - 第 6 位:
0 | 0 = 0 - 第 7 位:
1 | 1 = 1 - 第 8 位:
0 | 1 = 1
最终结果是 01011011。
3. 按位异或运算(XOR)
① 运算符:^
按位异或运算使用符号 ^ 表示。它也是一种双目运算符,需要两个操作数。
② 运算规则
按位异或运算的规则是:对应的两个二进位相异时,结果位为 1,相同时为 0。
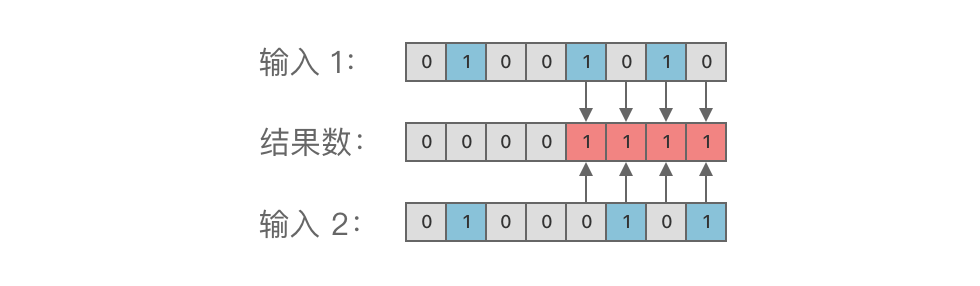
具体规则如下:
1 ^ 1 = 01 ^ 0 = 10 ^ 1 = 10 ^ 0 = 0
③ 示例
下例中我们理解按位异或运算:
01001010
^ 01000101
----------
00001111
逐位进行异或运算:
- 第 1 位:
0 ^ 1 = 1 - 第 2 位:
1 ^ 0 = 1 - 第 3 位:
0 ^ 0 = 0 - 第 4 位:
0 ^ 0 = 0 - 第 5 位:
1 ^ 0 = 1 - 第 6 位:
0 ^ 1 = 1 - 第 7 位:
1 ^ 0 = 1 - 第 8 位:
0 ^ 1 = 1
最终结果是 00001111。
4. 取反运算(NOT)
① 运算符:~
取反运算使用符号 ~ 表示。它是一种单目运算符,只需要一个操作数。
② 运算规则
取反运算的规则是:将 1 变为 0,0 变为 1。
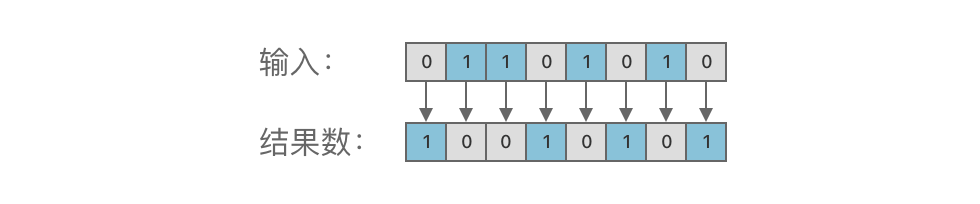
具体规则如下:
~0 = 1~1 = 0
③ 示例
让我们通过一个具体的例子来理解取反运算:
~01101010
----------
10010101
逐位进行取反运算:
- 第 1 位:
~0 = 1 - 第 2 位:
~1 = 0 - 第 3 位:
~1 = 0 - 第 4 位:
~0 = 1 - 第 5 位:
~1 = 0 - 第 6 位:
~0 = 1 - 第 7 位:
~1 = 0 - 第 8 位:
~0 = 1
最终结果是 10010101。
5. 左移运算(SHL)
① 运算符:<<
左移运算使用符号 << 表示。它是一种双目运算符,需要一个操作数和一个移位次数。
② 运算规则
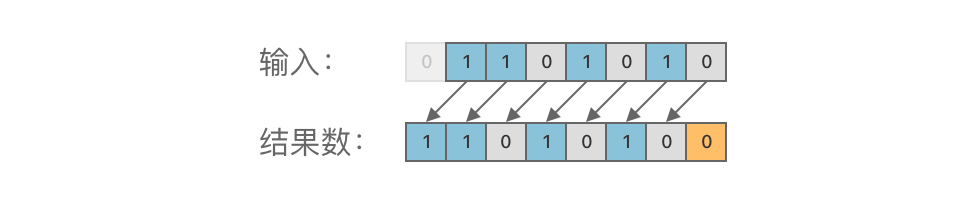
左移运算的规则是:将二进制数的各个二进位全部左移若干位,高位丢弃,低位补 0。
③ 示例:01101010 左移 1 位
让我们通过一个具体的例子来理解左移运算:
01101010 << 1
----------
11010100
逐位进行左移运算:
- 第 1 位:
0移出,高位丢弃 - 第 2 位:
1移到第 1 位 - 第 3 位:
1移到第 2 位 - 第 4 位:
0移到第 3 位 - 第 5 位:
1移到第 4 位 - 第 6 位:
0移到第 5 位 - 第 7 位:
1移到第 6 位 - 第 8 位:
0移到第 7 位 - 低位补
0
最终结果是 11010100。
6. 右移运算(SHR)
① 运算符:>>
右移运算使用符号 >> 表示。它也是一种双目运算符,需要一个操作数和一个移位次数。
② 运算规则
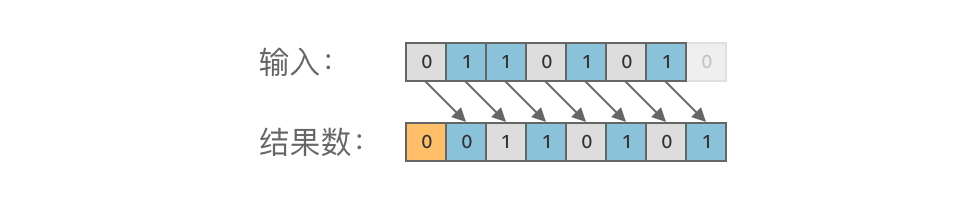
右移运算的规则是:将二进制数的各个二进位全部右移若干位,低位丢弃,高位补 0。
③ 示例:01101010 右移 1 位
让我们通过一个具体的例子来理解右移运算:
01101010 >> 1
----------
00110101
逐位进行右移运算:
- 第 8 位:
0移出,低位丢弃 - 第 7 位:
1移到第 8 位 - 第 6 位:
0移到第 7 位 - 第 5 位:
1移到第 6 位 - 第 4 位:
0移到第 5 位 - 第 3 位:
1移到第 4 位 - 第 2 位:
1移到第 3 位 - 第 1 位:
0移到第 2 位 - 高位补
0
最终结果是 00110101。
三、 位运算的应用
1. 位运算的常用操作
① 判断整数奇偶
原理:通过与 1 进行按位与运算
判断一个整数是奇数还是偶数,可以通过与 1 进行按位与运算。如果结果为 0,则该数为偶数;如果结果为 1,则该数为奇数。
示例:判断 x 是奇数还是偶数
def is_even(x):
return (x & 1) == 0
def is_odd(x):
return (x & 1) == 1
# 示例
x = 10
print(f"{x} 是偶数吗?", is_even(x)) # 输出:True
print(f"{x} 是奇数吗?", is_odd(x)) # 输出:False
思维流程

② 二进制数选取指定位
原理:使用按位与运算
要选取二进制数中的某几位,可以使用按位与运算。通过构造一个掩码(mask),掩码中对应选取位置为 1,其余位置为 0,然后与原二进制数进行按位与运算。
示例:取二进制数 01101010 的末尾 4 位
def get_last_n_bits(x, n):
mask = (1 << n) - 1
return x & mask
# 示例
x = 0b01101010
n = 4
result = get_last_n_bits(x, n)
print(f"二进制数 {bin(x)} 的末尾 {n} 位是 {bin(result)}") # 输出:0b1010
思维流程

③ 将指定位设置为 1
原理:使用按位或运算
要将二进制数中的某几位设置为 1,可以使用按位或运算。通过构造一个掩码,掩码中对应选取位置为 1,其余位置为 0,然后与原二进制数进行按位或运算。
**示例:将二进制数 01101010 的末尾 4 位设置为 **1
def set_last_n_bits(x, n):
mask = (1 << n) - 1
return x | mask
# 示例
x = 0b01101010
n = 4
result = set_last_n_bits(x, n)
print(f"二进制数 {bin(x)} 的末尾 {n} 位设置为 1 后是 {bin(result)}") # 输出:0b1111
④ 反转指定位
原理:使用按位异或运算
要反转二进制数中的某几位,可以使用按位异或运算。通过构造一个掩码,掩码中对应选取位置为 1,其余位置为 0,然后与原二进制数进行按位异或运算。
示例:将二进制数 01101010 的末尾 4 位反转
def invert_last_n_bits(x, n):
mask = (1 << n) - 1
return x ^ mask
# 示例
x = 0b01101010
n = 4
result = invert_last_n_bits(x, n)
print(f"二进制数 {bin(x)} 的末尾 {n} 位反转后是 {bin(result)}") # 输出:0b1100
⑤ 交换两个数
原理:使用按位异或运算
通过按位异或运算可以实现两个数的交换,而无需额外的变量。
示例:交换 a 和 b 的值
def swap_numbers(a, b):
a ^= b
b ^= a
a ^= b
return a, b
# 示例
a, b = 10, 20
a, b = swap_numbers(a, b)
print(f"交换后 a = {a}, b = {b}") # 输出:a = 20, b = 10
思维流程图

⑥ 将二进制最右侧为 1 的二进位改为 0
**原理:使用 **X & (X - 1)
要将二进制数中最右侧为 1 的二进位改为 0,可以使用 X & (X - 1) 操作。
**示例:将 01101100 最右侧的 1 改为 **0
def clear_rightmost_bit(x):
return x & (x - 1)
# 示例
x = 0b01101100
result = clear_rightmost_bit(x)
print(f"二进制数 {bin(x)} 最右侧的 1 改为 0 后是 {bin(result)}") # 输出:0b1101000
⑦ 计算二进制中二进位为 1 的个数
原理:使用 X & (X - 1) 统计次数
通过不断使用 X & (X - 1) 操作,可以将二进制数中最右侧为 1 的二进位改为 0,直到所有位都为 0。统计操作次数,即可得到二进制中 1 的个数。
示例:计算 01101100 中 1 的个数
def count_ones(x):
count = 0
while x:
x &= (x - 1)
count += 1
return count
# 示例
x = 0b01101100
result = count_ones(x)
print(f"二进制数 {bin(x)} 中 1 的个数是 {result}") # 输出:4
思维流程

⑧ 判断某数是否为 2 的幂次方
**原理:使用 **X & (X - 1) == 0
判断一个数是否为 2 的幂次方,可以通过 X & (X - 1) == 0 来实现。如果结果为 0,则该数是 2 的幂次方;否则,不是。
示例:判断 4 是否为 2 的幂次方
def is_power_of_two(x):
return (x & (x - 1)) == 0
# 示例
x = 4
result = is_power_of_two(x)
print(f"{x} 是 2 的幂次方吗? {result}") # 输出:True
思维流程

2. 位运算的常用操作总结
① 常用操作列表
| 功能 | 位运算符 | 示例 |
|---|---|---|
| 判断整数奇偶 | & | (x & 1) == 0 |
| 选取指定位 | & | x & ((1 << n) - 1) |
将指定位设置为 1 | ` | ` |
| 反转指定位 | ^ | x ^ ((1 << n) - 1) |
| 交换两个数 | ^ | a ^= b; b ^= a; a ^= b; |
将最右侧 1 改为 0 | & | x & (x - 1) |
计算 1 的个数 | & | while x: x &= (x - 1); count += 1 |
判断是否为 2 的幂次方 | & | (x & (x - 1)) == 0 |
3. 二进制枚举子集
① 二进制枚举子集简介
子集的概念
子集是指一个集合中的任意元素都是另一个集合的元素。例如,集合 {1, 2, 3} 的子集包括 {}、{1}、{2}、{3}、{1, 2}、{1, 3}、{2, 3}、{1, 2, 3}。
二进制枚举子集的原理
对于一个元素个数为
n的集合S,可以用一个长度为n的二进制数来表示其子集。每一位对应集合中的一个元素,1表示选取该元素,0表示不选取该元素。通过枚举0到2^n - 1的所有二进制数,可以得到集合S的所有子集。
② 二进制枚举子集代码
代码实现:枚举集合 S 的所有子集
def subsets(S):
n = len(S)
sub_sets = []
for i in range(1 << n):
sub_set = []
for j in range(n):
if i & (1 << j):
sub_set.append(S[j])
sub_sets.append(sub_set)
return sub_sets
# 示例
S = [1, 2, 3]
result = subsets(S)
print(f"集合 {S} 的所有子集是 {result}") # 输出:[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
思维流程图

Ok,今天我们就学习到这!😎👌
相关链接
- 项目地址:LeetCode-CookBook
- 相关文档:专栏地址
- 作者主页:GISer Liu-CSDN博客

如果觉得我的文章对您有帮助,三连+关注便是对我创作的最大鼓励!或者一个star🌟也可以😂.











![[Docker学习笔记]利用Dockerfile创建镜像](https://i-blog.csdnimg.cn/direct/f8f998b0cfd243b1929db9131296b235.png)



