---

题目链接：

611.有效三角形的个数

---

题目描述：

---

解法

数学知识：

给我们3个数，判断是否能够构成三角形。

平时：a+b>c，a+c>b，b+c>a（判断三次）

如果已知3个数的大小 ，我们可以只判断较小的两个数之和是否大于第三个数。（判断一次）

我们可以先对整个数组排序。

解法一（暴力求解）

三层 for 循环枚举出所有的三元组，并且判断是否能构成三角形。

如果能构成三角形，需要满足任意两边之和要大于第三边。但是实际上只需让较小的两条边之和大于第三边即可。

经过我们的优化后，暴力枚举法的时间复杂度从3n³变成了nlogn+n³。

解法二（排序 + 双指针）

排完序后，数组就有序了。我们就可以利用单调性使用双指针算法来解决问题。

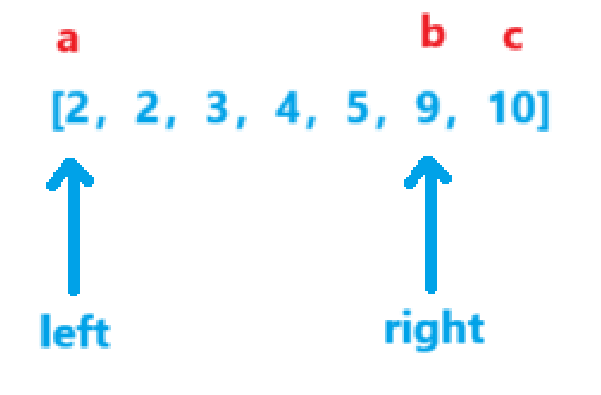
比如如果a，b，c取如图的位置。a+b>c，那么left往后移动，得到的结果都可以组成三角形。

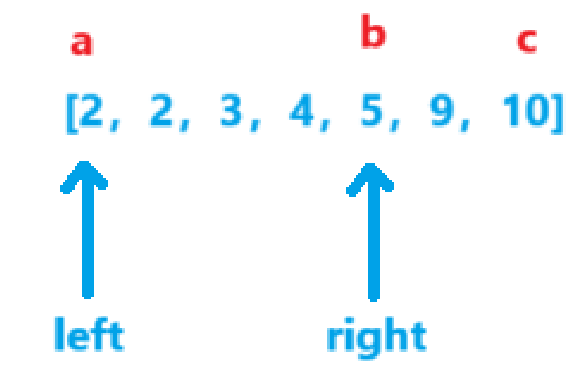
如果a，b，c取如图的位置。a+b<=c，那么无论left往后移动多少，得到的结果都不可以组成三角形。

步骤：

1. 先固定最大的数（固定n次）
2. 在最大的数的左区间内，使用双指针算法 ，快速统计出符合要求的三元组的个数。
3. 然后更换固定的最大的数 ，依次类推。

---

C++ 算法代码：

解法一（暴力求解）（会超时）O(nlogn+n³)

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        // 1. 排序
        sort(nums.begin(), nums.end());
        int n = nums.size(), ret = 0;
        // 2. 从小到大枚举所有的三元组
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                for (int k = j + 1; k < n; k++) {
                    // 当最小的两个边之和大于第三边的时候，统计答案
                    if (nums[i] + nums[j] > nums[k])
                        ret++;
                } 
            }
        }
        return ret;
    }
};

解法二（排序 + 双指针）O(n²)

class Solution 
{
public:
    int triangleNumber(vector<int>& nums) 
    {
        // 1. 优化，排序一下数组
        sort(nums.begin(), nums.end());
        // 2. 利用双指针解决问题
        int ret = 0, n = nums.size();
        for(int i = n - 1; i >= 2; i--) // 先固定最大的数，从后往前固定
        {
            // 利用双指针快速统计符合要求的三元组的个数
            int left = 0, right = i - 1;
            while(left < right)
            {
                if(nums[left] + nums[right] > nums[i]){
                    ret += right - left;
                    right--;
                }
                else{
                    left++;
                }
            }
        }
        return ret;
    }
};

---

图解：

nums=[2，2，3，4]

1. 优化，排序一下数组，原数组已经顺序了，所以没有变化。

2. 进入第一层循环，i=3，left=0，right=2

   nums[0] + nums[2] > nums[3]

   ret=ret + right - left=2

   right--，right=1

3. i=3，left=0，right=1

   nums[0] + nums[1] = nums[3]

   left++，left=1

   跳出while循环，i--

4. i=2，left=0，right=1

   nums[0] + nums[1] > nums[2]

   ret=ret + right - left=3

   right--，right=0

   跳出while循环，i--

5. i=1跳出外层for循环

6. ret=3