1.使用函数的递归方法,输出给定字符串的逆序,如"abcdefg",输出为“gfedcba”.
方法一:首先不采用递归的方法,如何完成上述要求
#include<stdio.h>
#include<string.h>
int main()
{
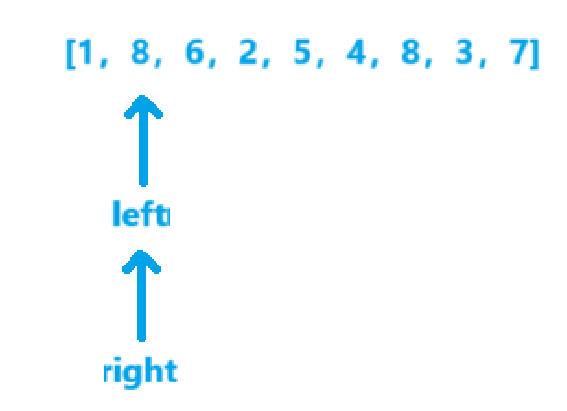
char arr[] = "abcdefg";
int sz = strlen(arr);
int left = 0;
int right = strlen(arr) - 1;
int temp = 0;
while (left < right)
{
temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
left++;
right--;
}
int i = 0;
for (i = 0;i<sz;i++)
{
printf("%c", arr[i]);
}
return 0;
}运行结果如下所示:

下面使用递归的方法进行逆序转化,代码如下:
#include<stdio.h>
#include<string.h>
void reverse_order(char* str)
{
char tmp = *str;
int len = strlen(str);
*str = *(str + len - 1);
*(str + len - 1) = '\0';
if (strlen(str + 1) >= 2)
{
reverse_order(str + 1);
}
*(str + len - 1) = tmp;
}
int main()
{
char arr[] = "abcdefghijk";
reverse_order(arr);
printf("%s\n", arr);
return 0;
}运行结果如下:

函数reverse_order的实现思路是利用递归,将字符串中的第一个和最后一个字符进行交换,然后不断缩小字符串的范围,直到字符串长度小于2。具体步骤如下:
- 首先将字符串中第一个字符保存到一个临时变量
tmp中。 - 获取字符串的长度,并将最后一个字符赋值给字符串的第一个字符。
- 将字符串的最后一个字符置为结束符
\0,相当于将原字符串的最后一个字符删除。 - 判断去掉第一个和最后一个字符的子串的长度是否大于等于2,如果是则递归调用
reverse_order函数,传入的参数为子串的首地址+1。 - 将之前保存的第一个字符赋值给字符串的最后一个字符。
- 最后,整个字符串的字符顺序就完成了反转。
上面的代码思路上可能有些复杂,也可以用下面一种方法
#include<stdio.h>
#include<string.h>
void reverse_order(char arr[],int left,int right)
{
char tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
if (left < right)
{
reverse_order(arr, left + 1, right - 1);
}
}
int main()
{
char arr[] = "abcdefghijk";
int left = 0;
int right = strlen(arr) - 1;
reverse_order(arr,left,right);
printf("%s\n", arr);
return 0;
}运行结果与上面的一致。
2.使用函数递归的方法计算一个数的每位数之和,例如输入1729,应该返回1+7+2+9=19.
#include<stdio.h>
int DigitSum(int input)
{
int sum = 0 ;
while (input % 10 != 0)
{
sum = sum + input % 10;
input = input / 10;
DigitSum(input);
}
return sum;
}
int main()
{
int input = 0;
scanf_s("%d", &input);
int ret = DigitSum(input);
printf("%d\n",ret);
return 0;
}运行结果如下:

3.使用递归方法,求一个数的k次方
代码如下:
#include<stdio.h>
double pow(int n, int k)
{
if (k > 0)
{
return pow(n, k-1) * n;
}
else if(k == 0)
{
return 1;
}
else
{
return 1.0 / pow(n, -k);
}
}
int main()
{
int n = 0;
int k = 0;
printf("请输入一个数和次幂:");
scanf_s("%d %d", &n,&k);
double ret = pow(n,k);
printf("%d的%d次方 = %1f\n", n,k, ret);
return 0;
}运行结果如下: