文章目录
- 题目链接:
- 题目描述:
- 解法
- C++ 算法代码:
- 图解:
题目链接:
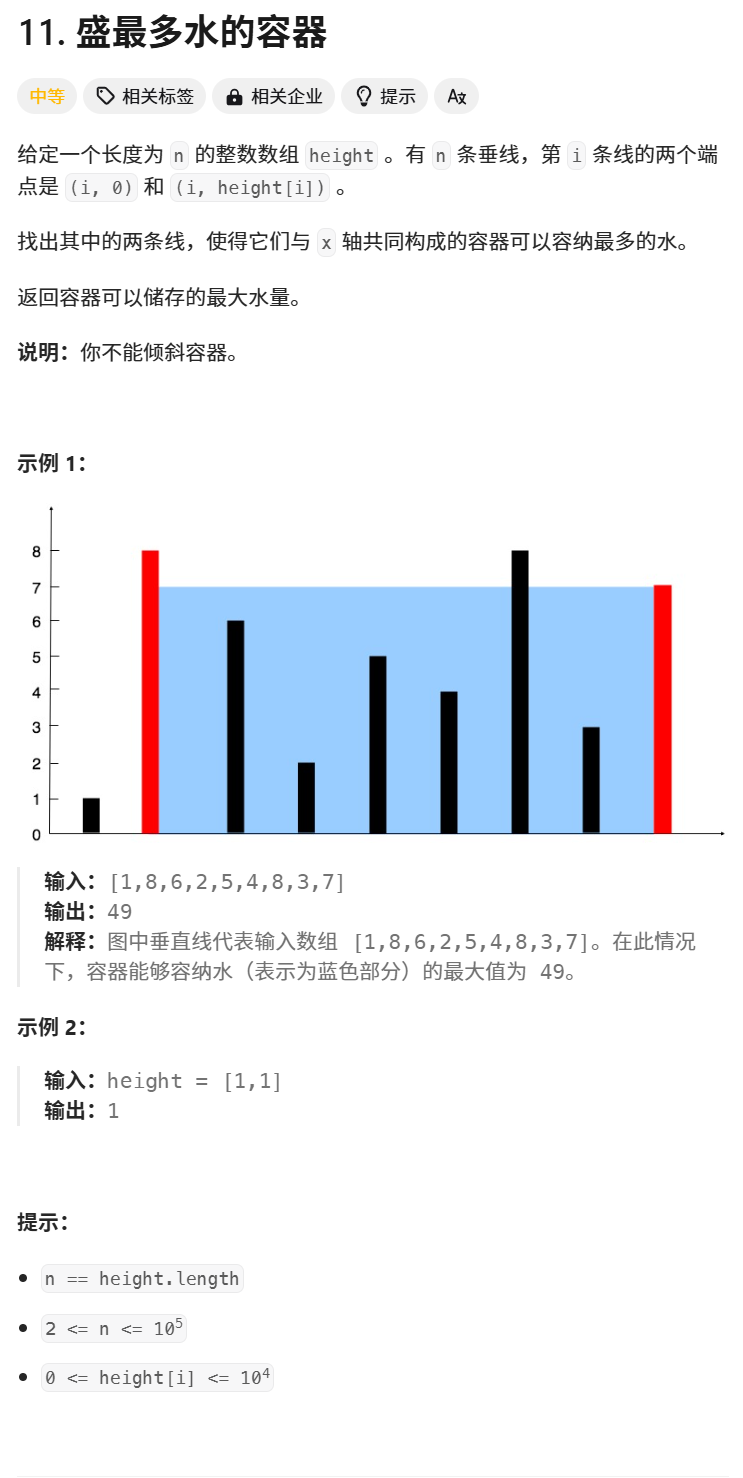
11.盛最多水的容器
题目描述:
解法
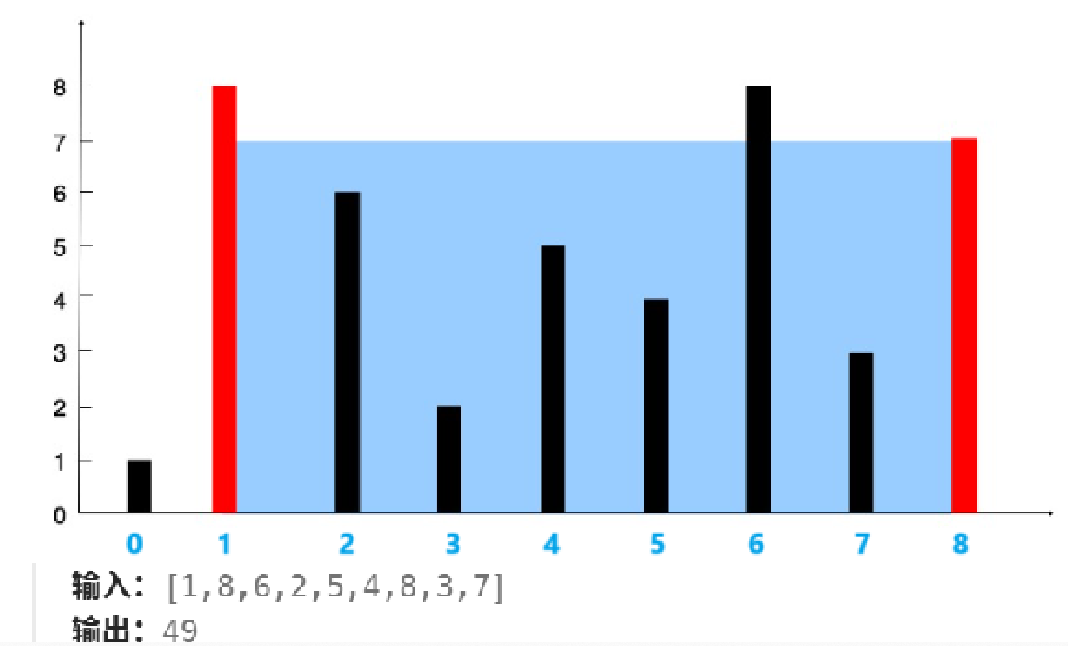
7x7=49
解法一:暴力枚举
输入:
[1,8,6,2,5,4,8,3,7]然后
1x8,1x6,1x2,1x5。。。依次类推,然后把所有得到的值比较,得到最大值。
解法二:对撞指针
v(体积)=h(高度)乘 w(宽度)
我们先取一小段来看一下规律:

比如4和2,4和5。为什么呢?因为2和5不但高度比6小 ,而且和4的宽度也比6小。
就算里面出现高度比6大的数,但是盛水是看高度小的那一方的。也就是在高度固定的时候要看宽度。
所以我们在选完6和4之后,可以把6和4的值保存下来,然后比较6和5的值。
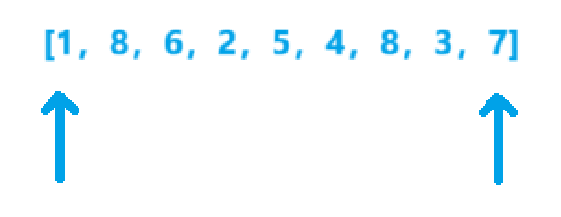
当遇到高度大于自己的,无论它多高都没用,重要的是看宽度。
所以1到7的乘水的容积是最大的,得到v1。
可以把1舍弃,直接从8开始看了。

继续重复,直到两个指针相遇,比较得到的一堆值。
C++ 算法代码:
解法一:暴力枚举(会超时)O(n2)
class Solution {
public:
int maxArea(vector<int>& height) {
int n = height.size();
int ret = 0;
// 两层 for 枚举出所有可能出现的情况
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// 计算容积,找出最大的那一个
ret = max(ret, min(height[i], height[j]) * (j - i));
}
}
return ret;
}
};
解法二:对撞指针 O(n)
class Solution
{
public:
int maxArea(vector<int>& height)
{
int left = 0, right = height.size() - 1, ret = 0;
while(left < right)
{
int v = min(height[left], height[right]) * (right - left);//计算容积v = h x w
ret = max(ret, v);//
// 移动指针
if(height[left] < height[right]){//谁小移动谁
left++;//左边小移动左边
}
else{
right--;//右边小或者一样大移动右边
}
}
return ret;
}
};
图解:
数组:[1,8,6,2,5,4,8,3,7]

- v=1x8=8,ret=8

- v=7x7=42,ret=49
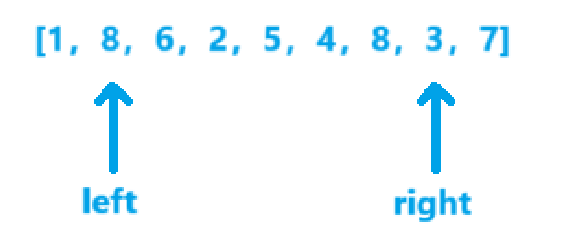
- v=3x6=18,ret=49
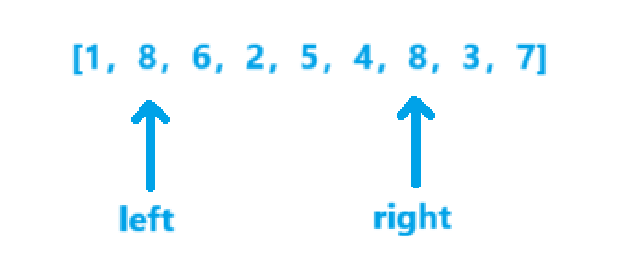
- v=8x5=40,ret=49
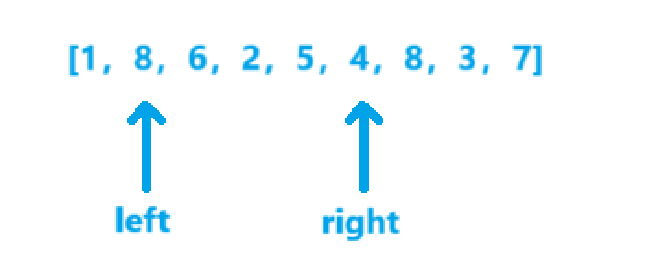
- v=4x4=16,ret=49
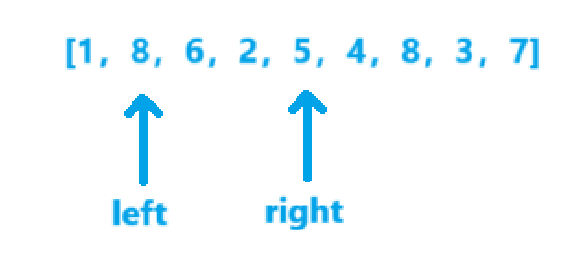
- v=5x3=15,ret=49
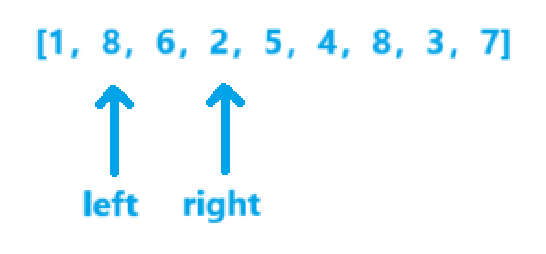
- v=2x2=4,ret=49
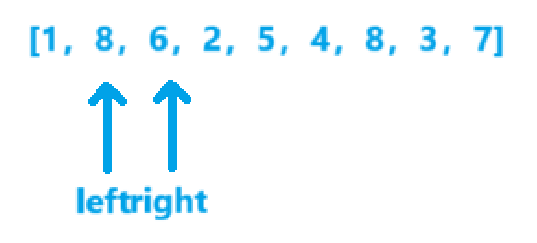
- v=6x1=6,ret=49
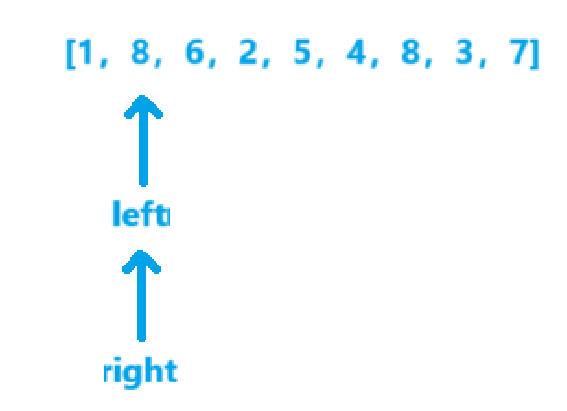
- 跳出循环,
return ret