8-回溯算法

参考

代码随想录

题目分类大纲如下：

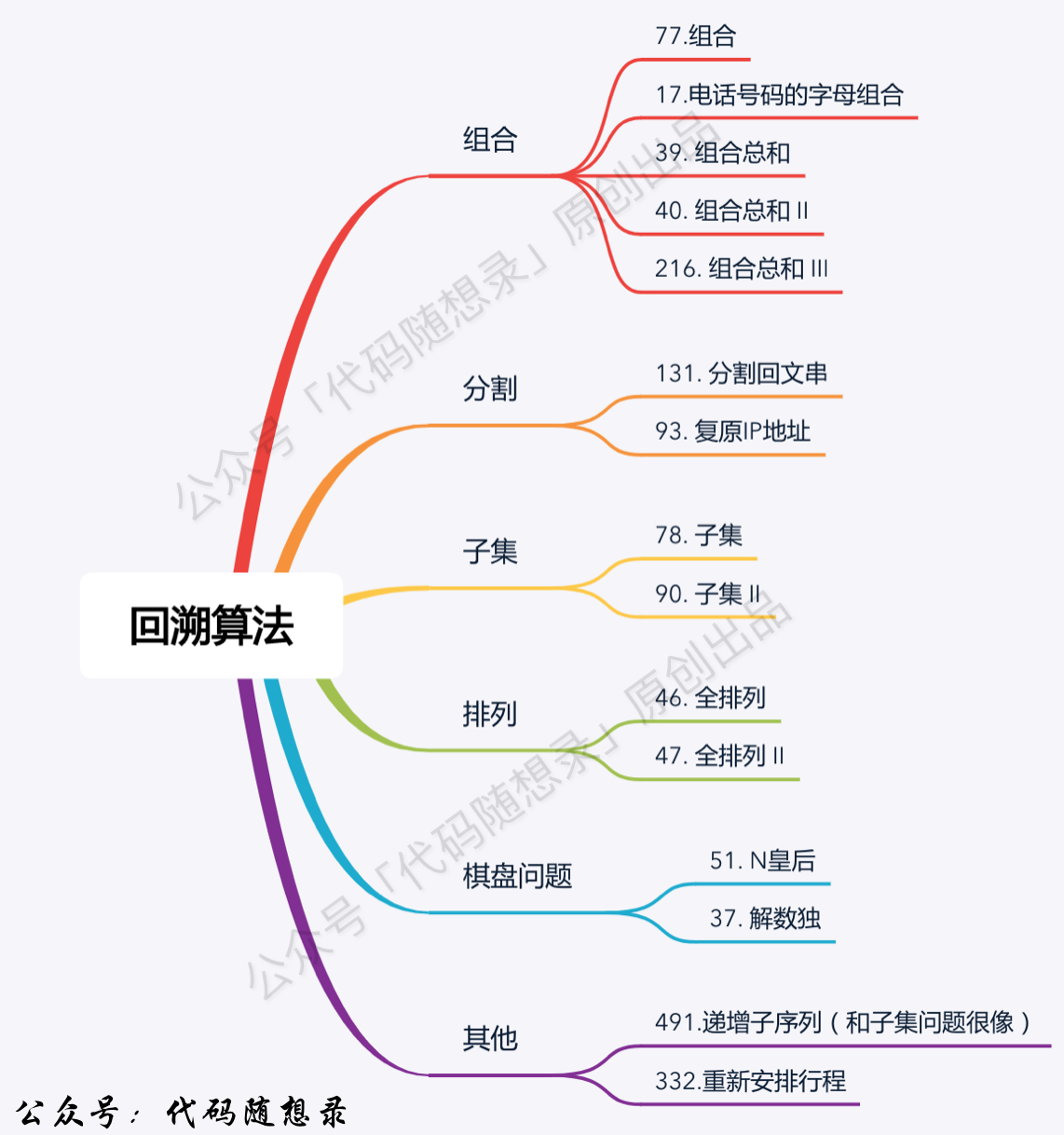
一、回溯算法理论基础

1、什么是回溯法

回溯法也可以叫做回溯搜索法，它是一种搜索的方式。回溯是递归的副产品，只要有递归就会有回溯。回溯法其实就是暴力查找，并不是什么高效的算法

2、回溯法的效率

虽然回溯法很难，很不好理解，但是回溯法并不是什么高效的算法。
因为回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

那么既然回溯法并不高效为什么还要用它呢？

因为没得选，一些问题能暴力搜出来就不错了，撑死了再剪枝一下，还没有更高效的解法。

3、回溯法解决的问题

回溯法，一般可以解决如下几种问题：

组合问题：N 个数里面按一定规则找出 k 个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个 N 个数的集合里有多少符合条件的子集
排列问题：N 个数按一定规则全排列，有几种排列方式
棋盘问题：N 皇后，解数独等等

组合是不强调元素顺序的，排列是强调元素顺序。

4、如何理解回溯法

回溯法解决的问题都可以抽象为树形结构，是的，所有回溯法的问题都可以抽象为树形结构！
因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。
递归就要有终止条件，所以必然是一棵高度有限的树（N 叉树）

5、回溯法模板

回溯三部曲：

（1）回溯函数模板返回值以及参数

回溯算法中函数返回值一般为 void
回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来，所以一般是先写逻辑，然后需要什么参数，就填什么参数

回溯函数伪代码如下：

void backtracking(参数)

（2）回溯函数终止条件

找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。

所以回溯函数终止条件伪代码如下：

if (终止条件) {
    存放结果;
    return;
}

（3）回溯搜索的遍历过程

回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。

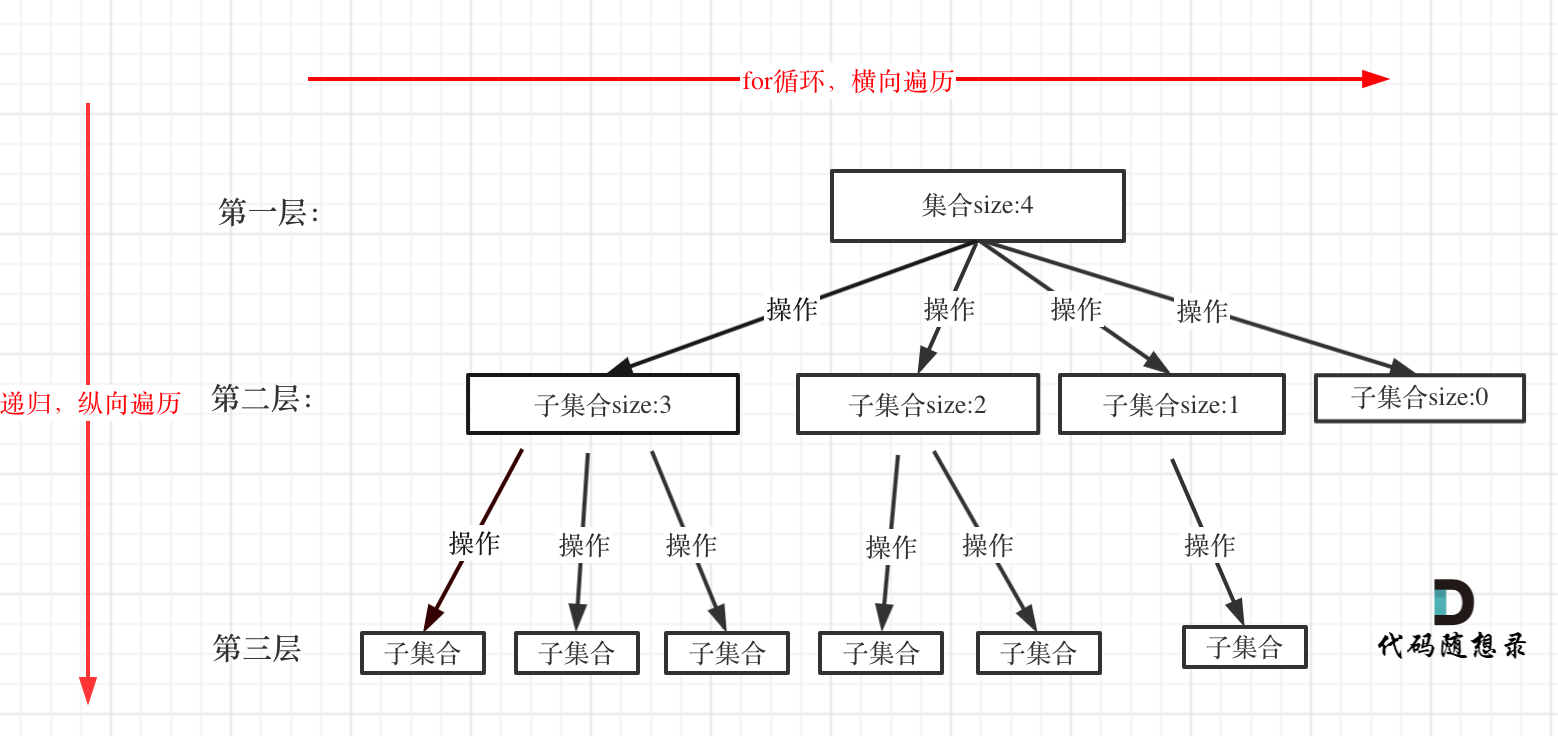
回溯函数遍历过程伪代码如下：

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

for 循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个 for 循环就执行多少次。
backtracking 这里自己调用自己，实现递归。
可以从图中看出 for 循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了

总结

分析完过程，回溯算法模板框架如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }


    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

二、组合问题

1、77.组合

参考：LeetCode–77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20
1 <= k <= n

递归

把回溯法的搜索过程抽象为树形结构，可以直观的看出搜索的过程。
接着用回溯法三部曲，逐步分析了函数参数、终止条件和单层搜索的过程

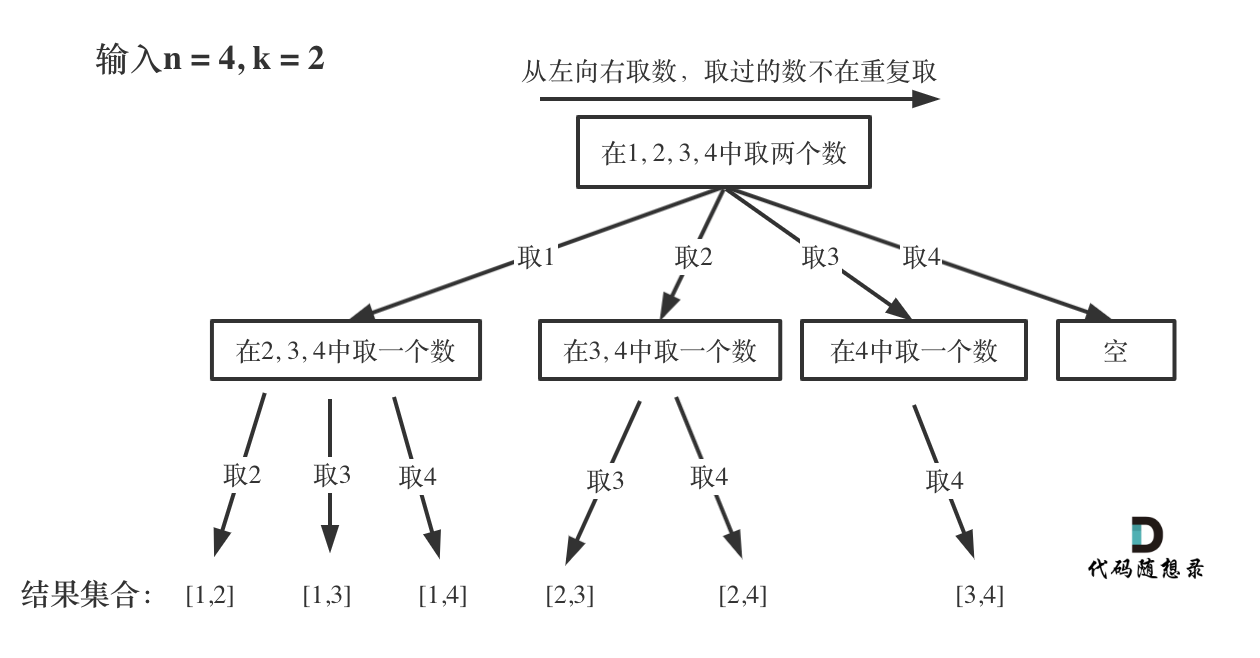
要解决 n 为 100，k 为 50 的情况，暴力写法需要嵌套 50 层 for 循环，那么回溯法就用递归来解决嵌套层数的问题。问题都可以抽象为树形结构（N 叉树），用树形结构来理解回溯就容易多了。那么我把组合问题抽象为如下树形结构：

java

import java.util.ArrayList;
import java.util.List;
public class LeetCode_77_backtrack {
    public List<List<Integer>> paths = new ArrayList<>();
    // 记录当前遍历的路径
    public List<Integer> path = new ArrayList<>();


    public List<List<Integer>> combine(int n, int k) {
        backtrack(n, k, 1);
        return paths;
    }


    public void backtrack(int n, int k, int startIndex) {
        // 递归终止条件是：path 的长度等于 k
        if (path.size() == k) {
            paths.add(new ArrayList<>(path));
            return;
        }
        // 横向遍历处理同一层结点，可能的搜索起点
        for (int i = startIndex; i <= n; i++) {
            // 处理当前结点
            path.add(i);
            // 纵向遍历处理下一层结点，并记录中间结果
            backtrack(n, k, i + 1);
            // 回退当前结点修改
            path.removeLast();
        }
    }
}

python

def combine(n, k):
    res = []
    path = []
    
    def backtrack(n, k, StartIndex):
        # 终止条件
        if len(path) == k:
            res.append(path[:])  # 结果保存
            return
        # 横向遍历
        for i in range(StartIndex, n + 1):
            path.append(i)  # 处理结点
            backtrack(n, k, i + 1)  # 纵向遍历
            path.pop()  # 回溯，撤销处理结果
            
    backtrack(n, k, 1)
    return res

递归-剪枝优化

回溯法虽然是暴力搜索，但也有时候可以有点剪枝优化一下的

举一个例子，n = 4，k = 4 的话，那么第一层 for 循环的时候，从元素 2 开始的遍历都没有意义了。在第二层 for 循环，从元素 3 开始的遍历都没有意义了。

这么说有点抽象，如图所示：

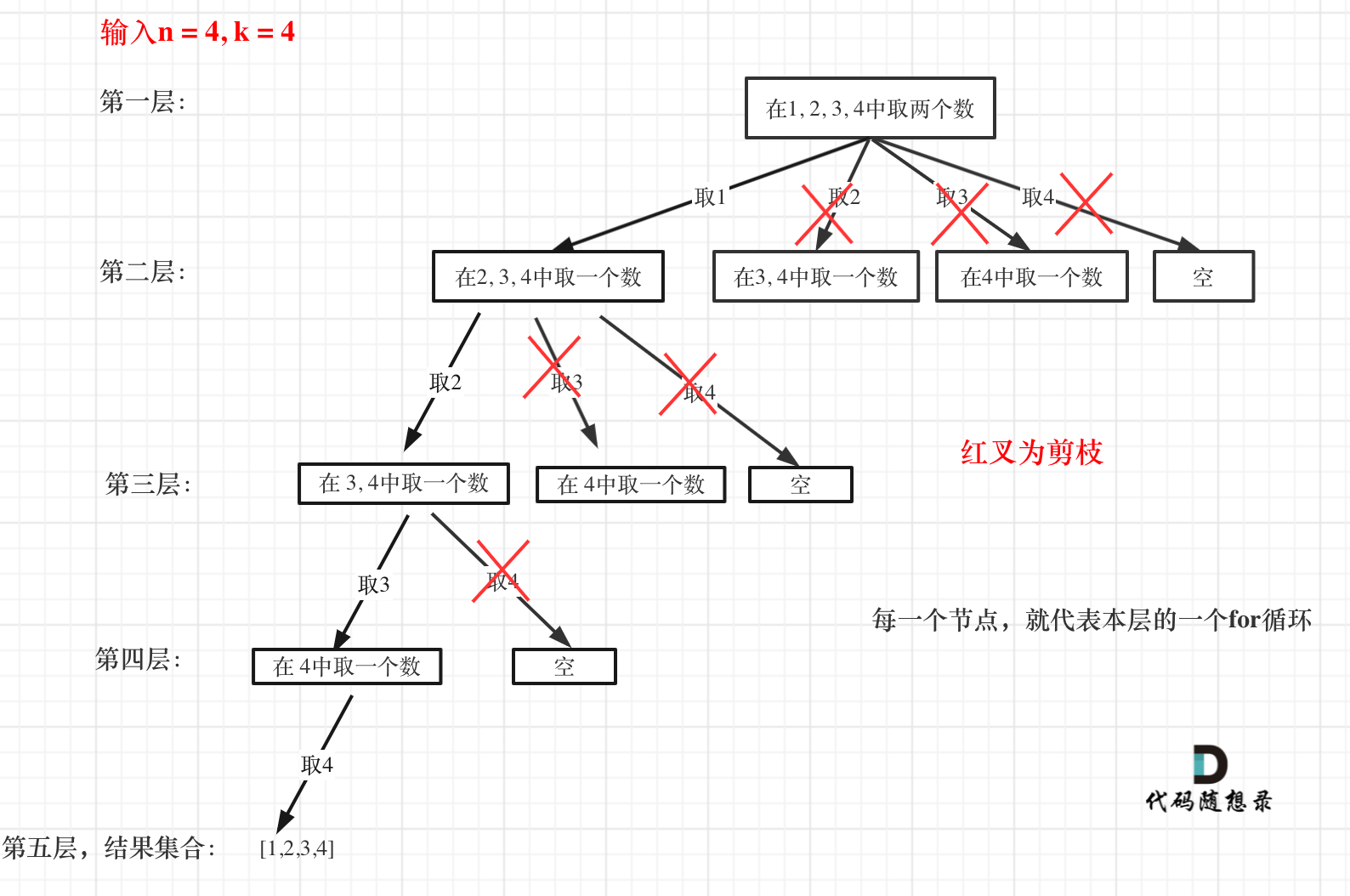
图中每一个节点（图中为矩形），就代表本层的一个 for 循环，那么每一层的 for 循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

所以，可以剪枝的地方就在递归中每一层的 for 循环所选择的起始位置。

如果 for 循环选择的起始位置之后的元素个数已经不足我们需要的元素个数了，那么就没有必要搜索了。

注意代码中 i，就是 for 循环里选择的起始位置。

for (int i = startIndex; i <= n; i++) {

接下来看一下优化过程如下：

已经选择的元素个数：path.size();
还需要的元素个数为: k - path.size();
在集合 n 中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

为什么有个+1 呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3，目前已经选取的元素为 0（path.size 为 0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从 2 开始搜索都是合理的，可以是组合[2, 3, 4]。

所以优化之后的 for 循环是：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i 为本次搜索的起始位置

java

import java.util.ArrayList;
import java.util.List;
public class LeetCode_77_backtrack {
    public List<List<Integer>> paths = new ArrayList<>();
    // 记录当前遍历的路径
    public List<Integer> path = new ArrayList<>();


    public List<List<Integer>> combine(int n, int k) {
        backtrack(n, k, 1);
        return paths;
    }


    public void backtrack(int n, int k, int startIndex) {
        // 递归终止条件是：path 的长度等于 k
        if (path.size() == k) {
            paths.add(new ArrayList<>(path));
            return;
        }
        // 横向遍历处理同一层结点，可能的搜索起点，起点位置要保证后续有足够的元素能构成k个元素
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) {
            // 处理当前结点
            path.add(i);
            // 纵向遍历处理下一层结点，并记录中间结果
            backtrack(n, k, i + 1);
            // 回退当前结点修改
            path.removeLast();
        }
    }
}

python

def combine(n, k):
    res = []  # 存放符合条件结果的集合
    path = []  # 用来存放符合条件结果
    
    def backtrack(n, k, startIndex):
        if len(path) == k:
            res.append(path[:])
            return
        for i in range(startIndex, n - (k - len(path)) + 2):  # 优化的地方
            path.append(i)  # 处理节点 
            backtrack(n, k, i + 1)  # 递归
            path.pop()  # 回溯，撤销处理的节点
            
    backtrack(n, k, 1)
    return res

2、216组合总和 III

LeetCode-- 216. 组合总和 III

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

所有数字都是正整数。
解集不能包含重复的组合。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]

递归

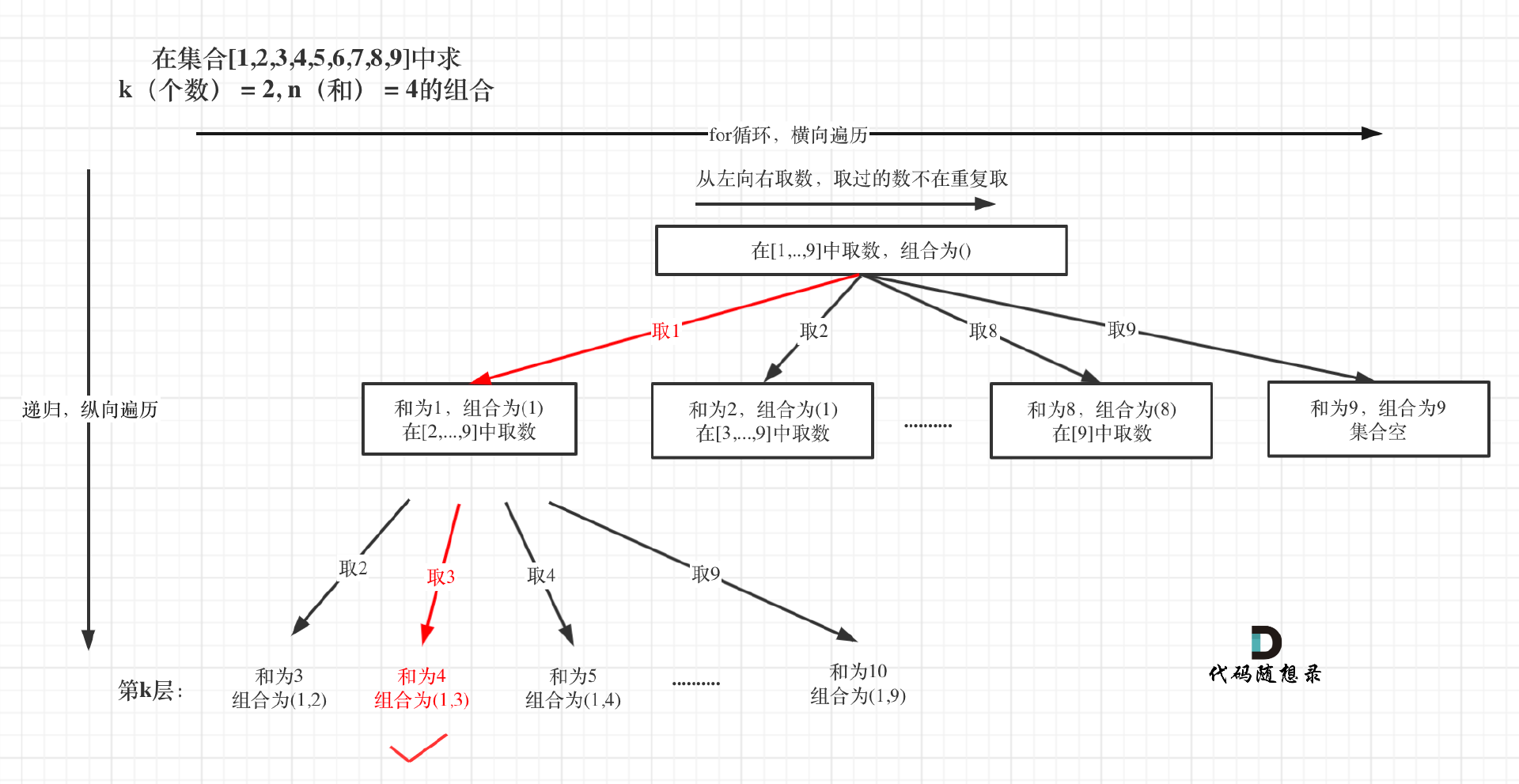
题目类似于上一题，无非就是多了一个限制，整个集合已经是固定的了[1,…,9]

选取过程如图：

剪枝

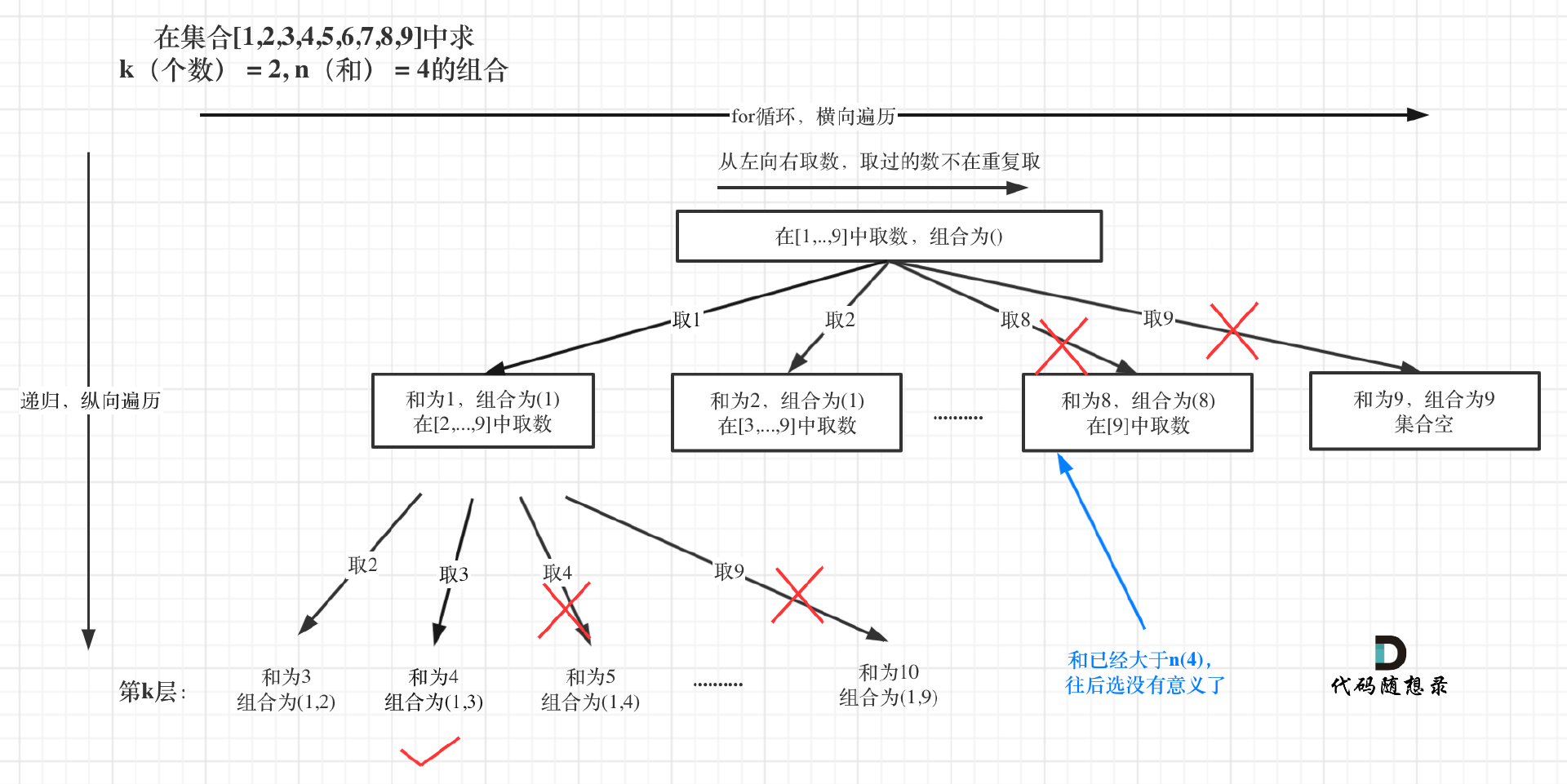
已选元素总和如果已经大于 n（图中数值为 4）了，那么往后遍历就没有意义了，直接剪掉。

那么剪枝的地方一定是在递归终止的地方剪，剪枝代码如下：

if (sum > targetSum) { // 剪枝操作
    return;
}

java

import java.util.ArrayList;
import java.util.List;
public class LeetCode_216_backtrack {
    public static void main(String[] args) {
        int k = 9;
        int n = 45;
        System.out.println(combinationSum3(k, n));
    }


    public static List<List<Integer>> paths = new ArrayList<>();
    public static List<Integer> path = new ArrayList<>();


    public static List<List<Integer>> combinationSum3(int k, int n) {
        backtrack(k, n, 1);
        return paths;
    }


    public static void backtrack(int k, int n, int startIndex) {
        // 递归出口，path长度为k、path元素和=n
        int sum = path.stream().mapToInt(Integer::intValue).sum();
        if (sum > n) {
            return;
        }
        if (path.size() == k) {
            if (sum == n) {
                paths.add(new ArrayList<>(path));
            }
            return;
        }
        // 横向遍历，以每个元素为起点构造组合，保证元素足够k个 且 path元素和<k
        for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
            if (path.stream().mapToInt(Integer::intValue).sum() + i > n) {
                return;
            }
            path.add(i);
            backtrack(k, n, i + 1);
            path.removeLast();
        }
    }
}

python

def combination(n, k):
    paths = []
    path = []
    def backtracking(n, k, startIndex):
        # 剪枝
        if sum(path) > n:
            return
        # 终止条件
        if len(path) == k:
            if sum(path) == n:
                paths.append(path[:])
            return
        # 遍历集合
        for i in range(startIndex, 10-(k-len(path)+1)):
            path.append(i)
            backtracking(n, k, i + 1)
            path.pop()
    backtracking(n, k, 1)
    return paths

3、17.电话号码的字母组合

参考：LeetCode–17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

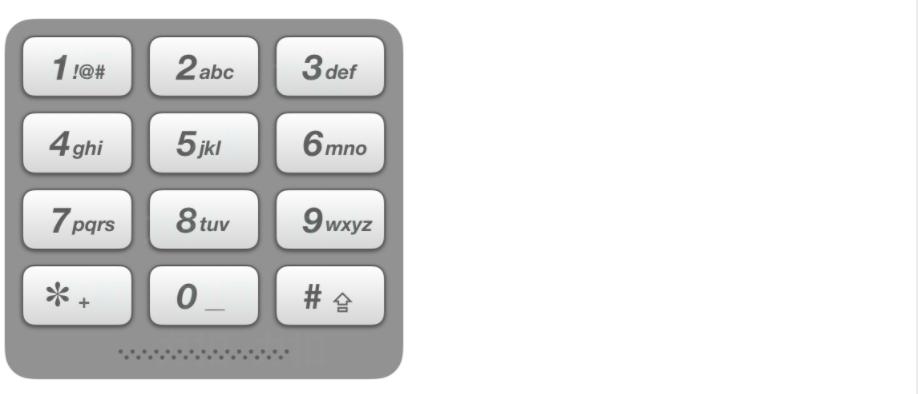
示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

递归

例如：输入：“23”，抽象为树形结构，如图所示：

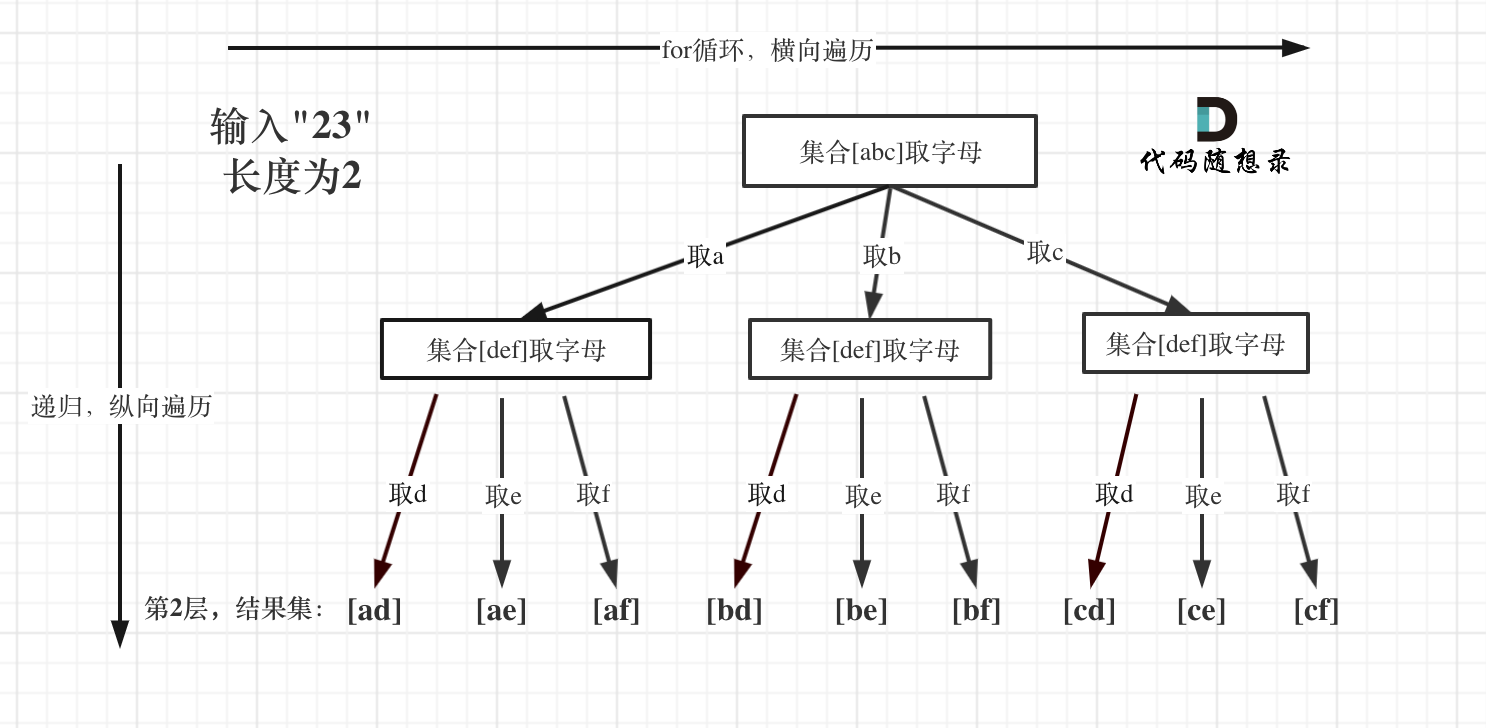
图中可以看出遍历的深度，就是输入"23"的长度，而叶子节点就是我们要收集的结果

java

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
public class LeetCode_17_backtrack {
    public static void main(String[] args) {
        String digits = "23";
        System.out.println(letterCombinations(digits));
    }


    public static List<String> paths = new ArrayList<>();
    public static StringBuilder path = new StringBuilder();
    public static Map<Character, String> digitToLetter = new HashMap<>() {{
        put('2', "abc");
        put('3', "def");
        put('4', "ghi");
        put('5', "jkl");
        put('6', "mno");
        put('7', "pqrs");
        put('8', "tuv");
        put('9', "wxyz");
    }};


    public static List<String> letterCombinations(String digits) {
        if (digits == null || digits.isEmpty()) {
            return paths;
        }
        backtrack(digits, 0);
        return paths;
    }


    public static void backtrack(String digits, int startIndex) {
        // 递归出口，path长度=digits长度
        if (path.length() == digits.length()) {
            paths.add(path.toString());
            return;
        }
        // 横向遍历，以数字对应的字母集合为起点
        String letter = digitToLetter.get(digits.charAt(startIndex));
        for (char ch : letter.toCharArray()) {
            path.append(ch);
            // 纵向遍历，遍历下一层的数字对应的字母
            backtrack(digits, startIndex + 1);
            path.deleteCharAt(startIndex);
        }
    }
}

复杂度分析

时间复杂度：O(3^m ×4^n)，其中 m 是输入中对应 3 个字母的数字个数（包括数字 2、3、4、5、6、8），n 是输入中对应 4 个字母的数字个数（包括数字 7、9），m+n 是输入数字的总个数。当输入包含 m 个对应 3 个字母的数字和 n 个对应 4 个字母的数字时，不同的字母组合一共有 3^m ×4^n 种，需要遍历每一种字母组合。
空间复杂度：O(m+n)，其中 m 是输入中对应 3 个字母的数字个数，n 是输入中对应 4 个字母的数字个数，m+n 是输入数字的总个数。除了返回值以外，空间复杂度主要取决于哈希表以及回溯过程中的递归调用层数，哈希表的大小与输入无关，可以看成常数，递归调用层数最大为 m+n。

python

def letterCombinations(digits):
    if not digits:
        return list()
    letter_map = {
        '2': 'abc',
        '3': 'def',
        '4': 'ghi',
        '5': 'jkl',
        '6': 'mno',
        '7': 'pqrs',
        '8': 'tuv',
        '9': 'wxyz'
    }
    res = []
    path = []
    
    def backtrack(digits, num):
        if len(path) == len(digits):
            res.append(''.join(path[:]))
            return
        for i in letter_map[digits[num]]:
            path.append(i)
            backtrack(digits, num+1)
            path.pop()
            
    backtrack(digits, 0)
    return res

4、39.组合总和

参考：LeetCode–39. 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些组合。

candidates 中的同一个数字可以 无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素互不相同
1 <= target <= 40

递归

本题没有数量要求，可以无限重复，但是有总和的限制，所以间接的也是有个数的限制。本题搜索的过程抽象成树形结构如下：

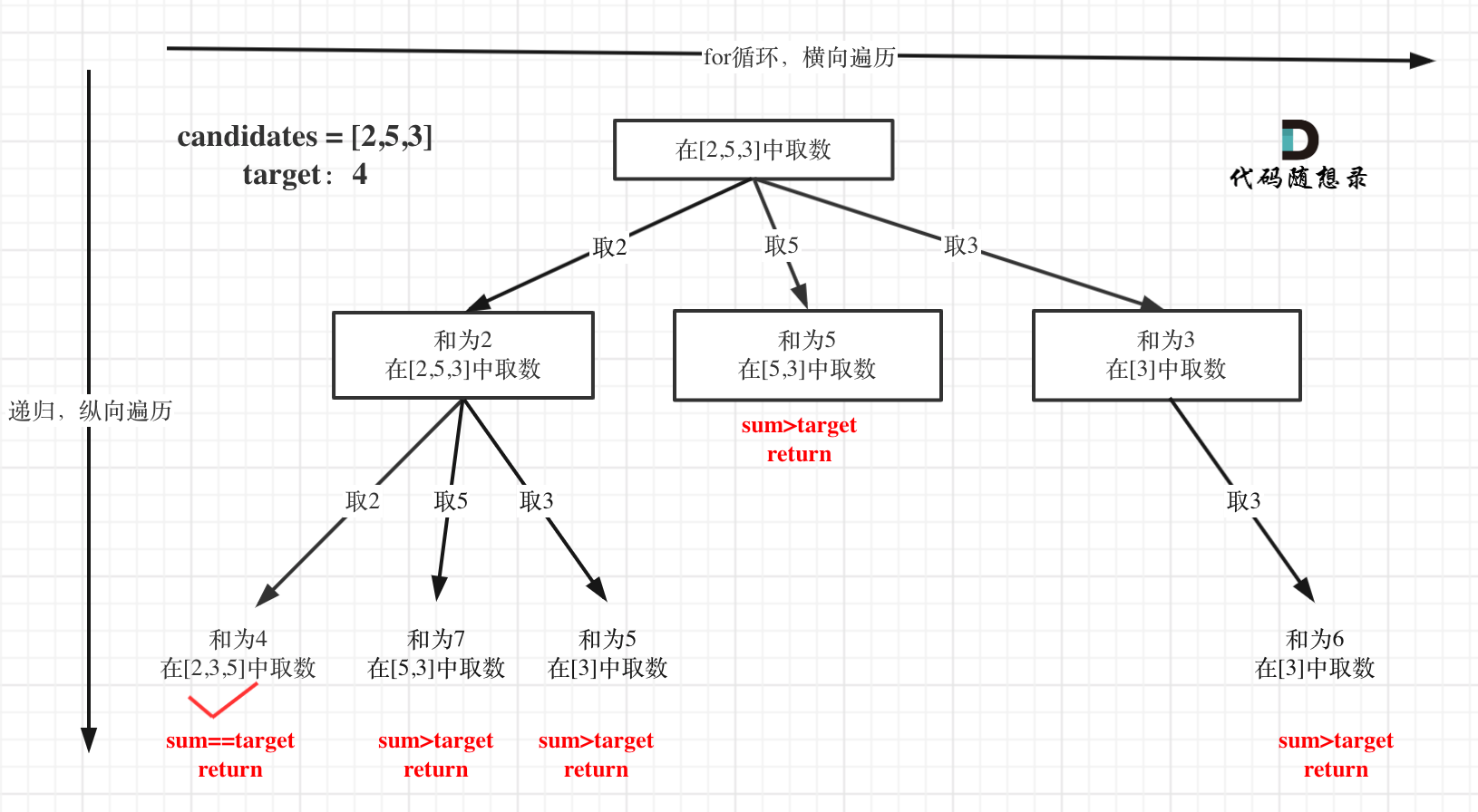
注意图中叶子节点的返回条件，因为本题没有组合数量要求，仅仅是总和的限制，所以递归没有层数的限制，只要选取的元素总和超过 target，就返回

java

import java.util.ArrayList;
import java.util.List;
public class LeetCode_39_backtrack {
    public static void main(String[] args) {
        int[] candidates = {2, 3, 6, 7};
        int target = 7;
        System.out.println(combinationSum(candidates, target));
    }


    public static List<List<Integer>> paths = new ArrayList<>();
    public static List<Integer> path = new ArrayList<>();


    public static List<List<Integer>> combinationSum(int[] candidates, int target) {
        backtrack(candidates, target, 0);
        return paths;
    }


    public static void backtrack(int[] candidates, int target, int startIndex) {
        // 递归出口，path和>=target
        int sum = path.stream().mapToInt(Integer::intValue).sum();
        if (sum >= target) {
            if (sum == target) {
                paths.add(new ArrayList<>(path));
            }
            return;
        }
        // 横向遍历，选取每个元素作为起点，元素可重复
        for (int i = startIndex; i < candidates.length; i++) {
            path.add(candidates[i]);
            backtrack(candidates, target, i);
            path.removeLast();
        }
    }
}

python

def combinationSum(candidates, target):
    paths = []
    path = []
    def backtracking(candidates, target, startIndex, sum_):
        # 结束条件
        if sum_ >= target:
            if sum_ == target:
                paths.append(path[:])
            return
        # 单层递归逻辑
        for i in range(startIndex, len(candidates)):
            sum_ += candidates[i]
            path.append(candidates[i])
            # 因为无限制重复选取，所以不是 i+1
            backtracking(candidates, target, i, sum_)
            sum_ -= candidates[i]
            path.pop()
        return
    
    backtracking(candidates, target, 0, 0)
    return paths

递归-剪枝优化

在上面这个树形结构中：上面的版本一的代码大家可以看到，对于 sum 已经大于 target 的情况，其实是依然进入了下一层递归，只是下一层递归结束判断的时候，会判断 sum > target 的话就返回。

其实如果已经知道下一层的 sum 会大于 target，就没有必要进入下一层递归了。
那么可以在 for 循环的搜索范围上做做文章了。
对总集合排序之后，如果下一层的 sum（就是本层的 sum + candidates[i]）已经大于 target，就可以结束本轮 for 循环的遍历。

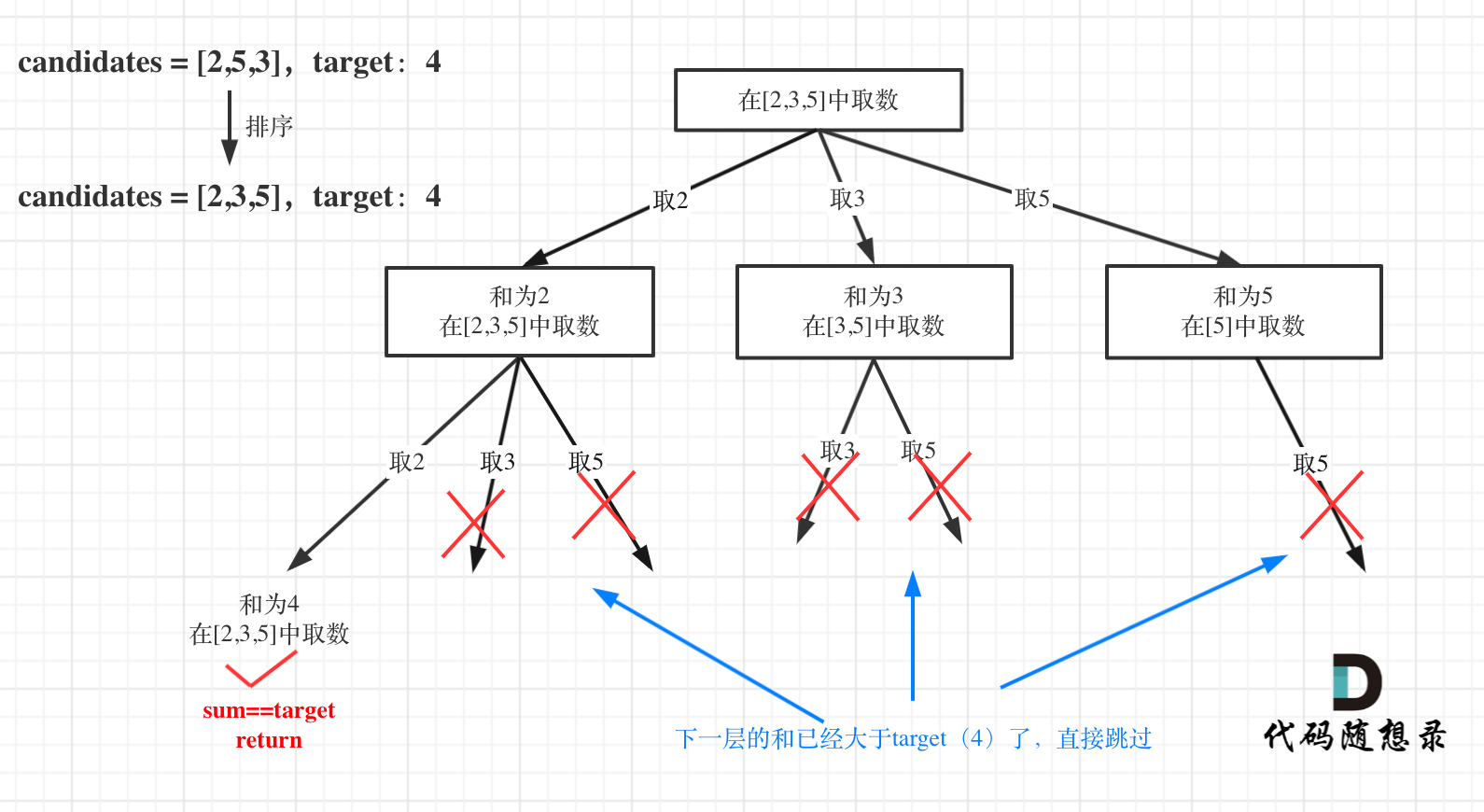
java

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class LeetCode_39_backtrack_2 {
    public static void main(String[] args) {
        int[] candidates = {2, 3, 6, 7};
        int target = 7;
        System.out.println(combinationSum(candidates, target));
    }


    public static List<List<Integer>> paths = new ArrayList<>();
    public static List<Integer> path = new ArrayList<>();


    public static List<List<Integer>> combinationSum(int[] candidates, int target) {
        // 为剪枝提前进行排序
        Arrays.sort(candidates);
        backtrack(candidates, target, 0, 0);
        return paths;
    }


    public static void backtrack(int[] candidates, int target, int startIndex, int sum) {
        // 递归出口，当前路径path的sum>=target
        if (sum >= target) {
            if (sum == target) {
                paths.add(new ArrayList<>(path));
            }
            return;
        }
        // 横向遍历，每个元素作为路径起点，元素可重复使用
        int candidate;
        for (int i = startIndex; i < candidates.length; i++) {
            candidate = candidates[i];
            // 剪枝操作，如果当前元素加上sum超过了target，后续元素更大所以更无法找到符合条件的path
            if (sum + candidate > target) {
                return;
            }
            path.add(candidate);
            sum += candidate;
            // 纵向遍历，向下一层元素遍历。无限制重复选取，所以不是 i+1
            backtrack(candidates, target, i, sum);
            // 一次遍历结束，回溯
            sum -= candidate;
            path.removeLast();
        }
    }
}

python

def combinationSum(candidates, target):
    paths = []
    path = []
    def backtracking(candidates, target, startIndex, sum_):
        # 结束条件
        if sum_ >= target:
            if sum_ == target:
                paths.append(path[:])
            return
        # 单层递归逻辑
        for i in range(startIndex, len(candidates)):
            # 剪枝，提前结束循环
            if sum_ + candidates[i] > target:
                return
            sum_ += candidates[i]
            path.append(candidates[i])
            # 因为无限制重复选取，所以不是 i+1
            backtracking(candidates, target, i, sum_)
            sum_ -= candidates[i]
            path.pop()
        return
    # 为剪枝提前进行排序
    backtracking(sorted(candidates), target, 0, 0)
    return paths

5、40.组合总和 II

参考：LeetCode-- 40. 组合总和 II

给定一个数组 candidates 和一个目标数 target，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

递归

本题的难点在于集合（数组 candidates）有重复元素，但还不能有重复的组合。把所有组合求出来，再用 set 或者 map 去重，这么做很容易超时！所以要在搜索的过程中就去掉重复组合。所谓去重，其实就是使用过的元素不能重复选取。

元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

为了理解去重我们来举一个例子，candidates = [1, 1, 2], target = 3，（方便起见 candidates 已经排序了）强调一下，树层去重的话，需要对数组排序！

选择过程树形结构如图所示：

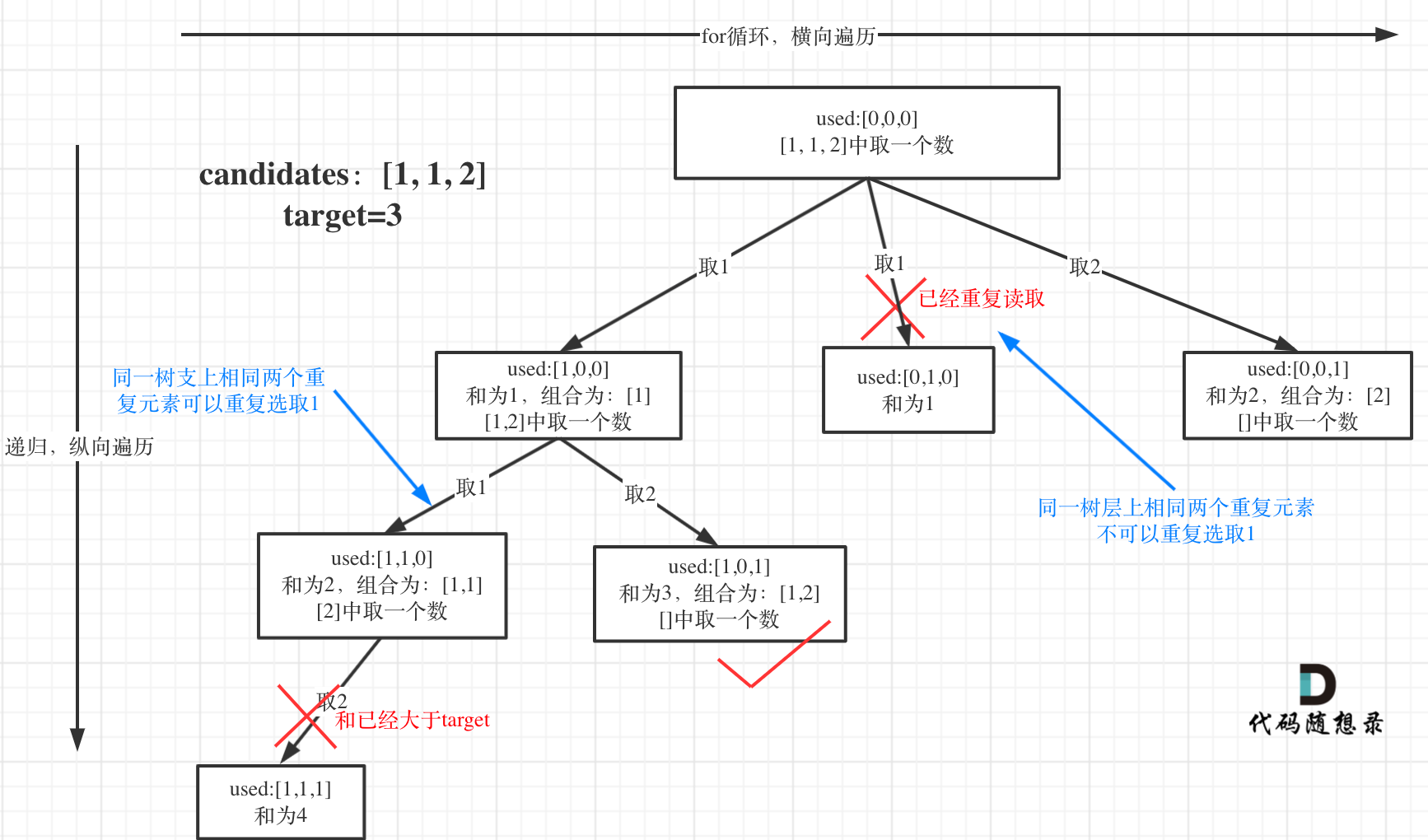
java

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class LeetCode_40_backtrack {
    public static void main(String[] args) {
        int[] candidates = {10, 1, 2, 7, 6, 1, 5};
        int target = 8;
        System.out.println(combinationSum2(candidates, target));
    }


    public static List<List<Integer>> paths = new ArrayList<>();
    public static List<Integer> path = new ArrayList<>();


    public static List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        backtrack(candidates, target, 0, 0);
        return paths;
    }


    public static void backtrack(int[] candidates, int target, int startIndex, int sum) {
        // 递归出口，路径path元素之和>=target
        if (sum >= target) {
            if (sum == target) {
                paths.add(new ArrayList<>(path));
            }
            return;
        }
        // 横向遍历，每个元素作为起点，数组中有重复元素，但是路径中不可有重复元素
        int candidate;
        for (int i = startIndex; i < candidates.length; i++) {
            candidate = candidates[i];
            // 同一层起点相同的不重复遍历
            if (i > startIndex && candidate == candidates[i - 1]) {
                continue;
            }
            // 剪枝操作
            if (sum + candidate > target) {
                return;
            }
            path.add(candidate);
            sum += candidate;
            // 纵向遍历，遍历下一层的元素
            backtrack(candidates, target, i + 1, sum);
            // 当前路径遍历结束，回溯
            sum -= candidate;
            path.removeLast();
        }
    }
}

python

def combinationSum(candidates, target):
    paths = []
    path = []
    def backtracking(candidates, target, sum_, startIndex):
        if sum_ >= target:
            if sum_ == target:
                paths.append(path[:])
            return
        for i in range(startIndex, len(candidates)):
            # 剪枝
            if sum_ + candidates[i] > target:
                return
            # 跳过同一树层使用过的元素
            if i > startIndex and candidates[i] == candidates[i-1]:
                continue
            sum_ += candidates[i]
            path.append(candidates[i])
            backtracking(candidates, target, sum_, i + 1)
            sum_ -= candidates[i]
            path.pop()
            
    backtracking(candidates, target, 0, 0)
    return paths

递归-used数组去重

class Solution:
    def __init__(self):
        self.paths = []
        self.path = []
        self.used = []
    def combinationSum2(self, candidates, target):
        '''
        类似于求三数之和，求四数之和，为了避免重复组合，需要提前进行数组排序
        本题需要使用 used，用来标记区别同一树层的元素使用重复情况：注意区分递归纵向遍历遇到的重复元素，和 for 循环遇到的重复元素，这两者的区别
        '''
        self.paths.clear()
        self.path.clear()
        self.usage_list = [False] * len(candidates)
        # 必须提前进行数组排序，避免重复
        candidates.sort()
        self.backtracking(candidates, target, 0, 0)
        return self.paths
        
    def backtracking(self, candidates, target, sum_, start_index):
        # Base Case
        if sum_ == target:
            self.paths.append(self.path[:])
            return
        # 单层递归逻辑
        for i in range(start_index, len(candidates)):
            # 剪枝，同 39.组合总和
            if sum_ + candidates[i] > target:
                return
            # 检查同一树层是否出现曾经使用过的相同元素
            # 若数组中前后元素值相同，但前者却未被使用(used == False)，说明是 for loop 中的同一树层的相同元素情况
            if i > 0 and candidates[i] == candidates[i - 1] and self.usage_list[i - 1] == False:
                continue
            sum_ += candidates[i]
            self.path.append(candidates[i])
            self.usage_list[i] = True
            self.backtracking(candidates, target, sum_, i + 1)
            self.usage_list[i] = False  # 回溯，为了下一轮 for loop
            self.path.pop()  # 回溯，为了下一轮 for loop
            sum_ -= candidates[i]  # 回溯，为了下一轮 for loop

三、排列问题

6、46.全排列

参考：LeetCode-- 46. 全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

回溯

以[1,2,3]为例，抽象成树形结构如下：

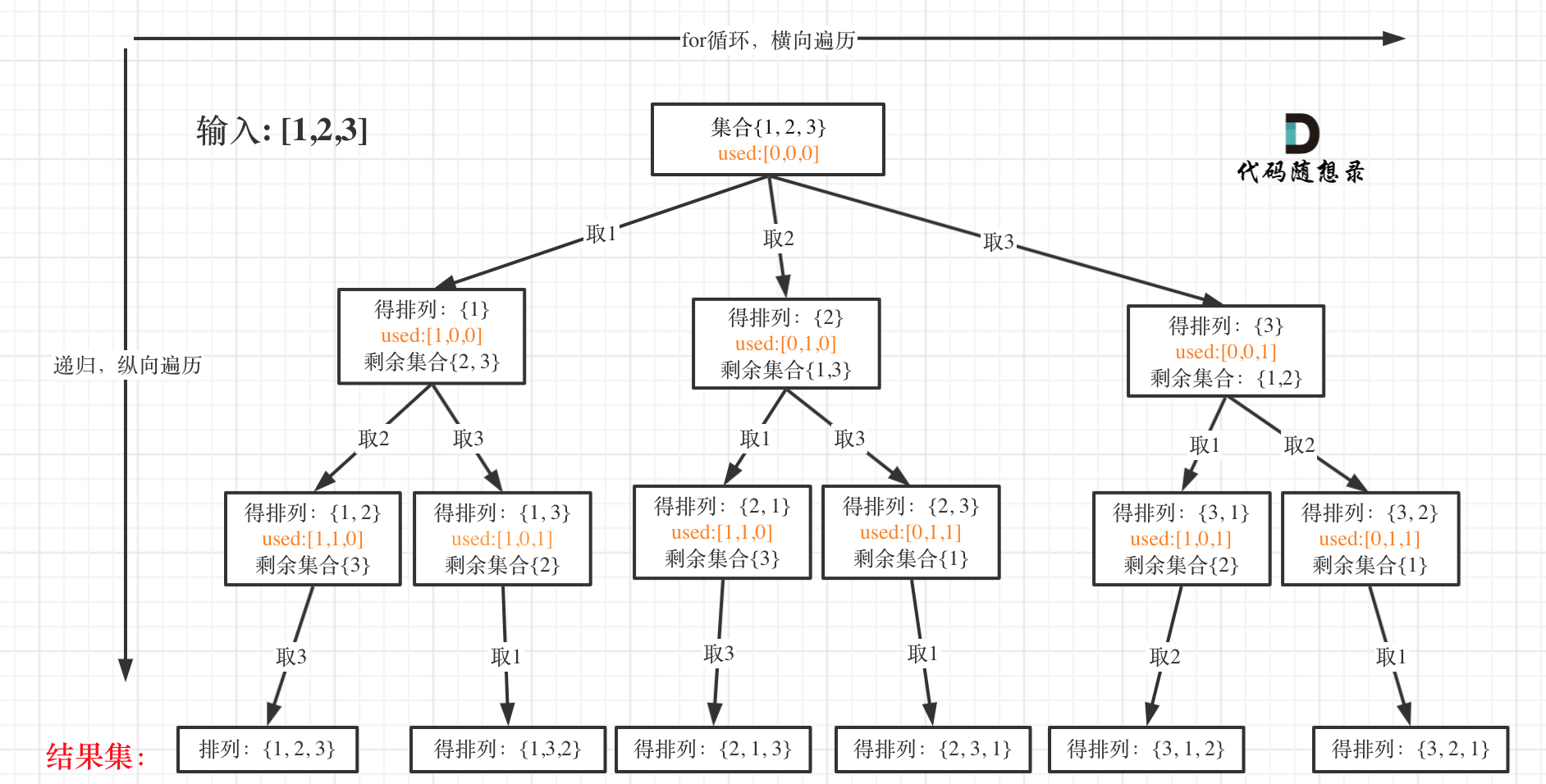
排列问题：

每层都是从 0 开始搜索而不是 startIndex
需要 used 数组记录 path 里都放了哪些元素了

回溯三部曲

(1)递归函数参数

先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合。
可以看出元素 1 在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次 1，所以处理排列问题就不用使用 startIndex 了。
但排列问题需要一个 used 数组，标记已经选择的元素，如图橘黄色部分所示

(2)递归终止条件

可以看出叶子节点，就是收割结果的地方。当收集元素的数组 path 的大小达到和 nums 数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。

(3)单层搜索的逻辑

最大的不同就是 for 循环里不用 startIndex 了。因为排列问题，每次都要从头开始搜索，例如元素 1 在[1,2]中已经使用过了，但是在[2,1]中还要再使用一次 1。
used 数组，其实就是记录此时 path 里都有哪些元素使用了，一个排列里一个元素只能使用一次。

java

import java.util.ArrayList;
import java.util.List;
public class LeetCode_46_backtrack {
    public static void main(String[] args) {
        int[] nums = {1, 2, 3};
        System.out.println(permute(nums));
    }


    public static List<List<Integer>> paths = new ArrayList<>();
    public static List<Integer> path = new ArrayList<>();


    public static List<List<Integer>> permute(int[] nums) {
        boolean[] used = new boolean[nums.length];
        backtrack(nums, used);
        return paths;
    }


    public static void backtrack(int[] nums, boolean[] used) {
        int n = nums.length;
        // 递归出口，path长度=nums长度
        if (path.size() == n) {
            paths.add(new ArrayList<>(path));
            return;
        }
        // 横向遍历，每个元素作为起点，遍历过的元素做标记
        for (int i = 0; i < n; i++) {
            if (used[i]) {
                continue;
            }
            path.add(nums[i]);
            used[i] = true;
            // 纵向遍历，从下一层中选取没有遍历过的元素
            backtrack(nums, used);
            // 回溯，当前路径遍历结束
            used[i] = false;
            path.removeLast();
        }
    }
}

python

def permute(nums):
    '''
    所以处理排列问题每层都需要从头搜索，故不再使用 start_index
    '''
    def backtracking(nums, usage_list):
        # 结束条件
        if len(path) == len(nums):
            paths.append(path[:])
            return


        # 单层递归逻辑
        for i in range(len(nums)):  # 从头开始搜索
            # 若遇到 path 里已收录的元素，跳过
            if usage_list[i] == True:
                continue
            usage_list[i] = True
            path.append(nums[i])
            backtracking(nums, usage_list)     # 纵向传递使用信息，去重
            path.pop()
            usage_list[i] = False
    
    path = []
    paths = []
    usage_list = [False] * len(nums)
    backtracking(nums, usage_list)
    return paths

回溯+丢掉 usage_list

def permute(nums) -> list:
    def backtracking(nums):
        # Base Case 本题求叶子节点
        if len(path) == len(nums):
            paths.append(path[:])
            return


        # 单层递归逻辑
        for i in range(0, len(nums)):  # 从头开始搜索
            # 若遇到 path 里已收录的元素，跳过
            if nums[i] in path:
                continue
            path.append(nums[i])
            backtracking(nums)
            path.pop()
    
    path = []
    paths = []
    backtracking(nums)
    return paths

7、47.全排列 II

参考：LeetCode-- 47. 全排列 II

给定一个可包含重复数字的序列 nums，按任意顺序返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

回溯

这道题目与上一题的区别在与给定一个可包含重复数字的序列，要返回所有不重复的全排列。这里又涉及到去重了。

去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

我以示例中的 [1,1,2]为例（为了方便举例，已经排序）抽象为一棵树，去重过程如图：

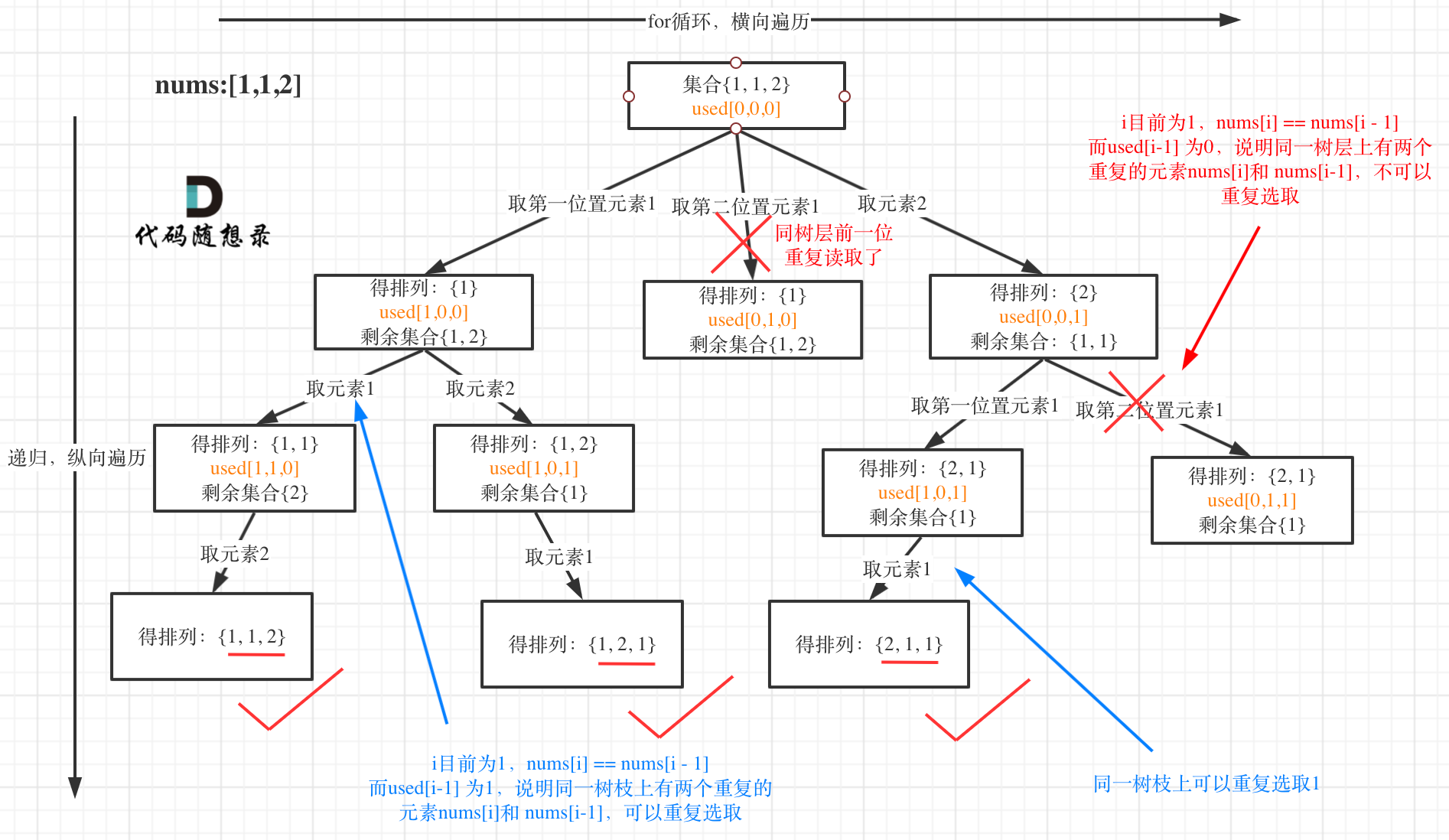
图中我们对同一树层，前一位（也就是 nums[i-1]）如果使用过，那么就进行去重。

一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。

去重最为关键的代码为：（树层上去重）

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
    continue;
}

java

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class LeetCode_47_backtrack {
    public static void main(String[] args) {
        int[] nums = {1, 1, 2};
        System.out.println(permuteUnique(nums));
    }


    public static List<List<Integer>> paths = new ArrayList<>();
    public static List<Integer> path = new ArrayList<>();


    public static List<List<Integer>> permuteUnique(int[] nums) {
        boolean[] used = new boolean[nums.length];
        // 数组排序，后续通过和上一个元素比较判断是否为重复的起点
        Arrays.sort(nums);
        backtrack(nums, used);
        return paths;
    }


    public static void backtrack(int[] nums, boolean[] used) {
        int n = nums.length;
        // 递归出口，path长度=nums长度
        if (path.size() == n) {
            paths.add(new ArrayList<>(path));
        }
        // 横向遍历，每个元素作为起点，重复的起点跳过
        for (int i = 0; i < n; i++) {
            // 同一层重复的结点跳过遍历
            if (used[i] || (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])) {
                continue;
            }
            path.add(nums[i]);
            used[i] = true;
            // 纵向遍历，向下一层结点遍历
            backtrack(nums, used);
            // 回溯，当前路径遍历结束
            used[i] = false;
            path.removeLast();
        }
    }
}

python

def permuteUnique(nums):
    # res 用来存放结果
    if not nums: return []
    res = []
    used = [0] * len(nums)
    def backtracking(nums, used, path):
        # 终止条件
        if len(path) == len(nums):
            res.append(path.copy())
            return
        for i in range(len(nums)):
            if not used[i]:
                # 如果同⼀树层 nums[i - 1]使⽤过则直接跳过
                if i>0 and nums[i]==nums[i-1] and not used[i-1]:
                    continue
                used[i] = 1
                path.append(nums[i])
                backtracking(nums, used, path)
                used[i] = 0
                path.pop()
                
    # 记得给 nums 排序
    backtracking(sorted(nums),used,[])
    return res

三、切割问题

8、131.分割回文串

参考：

LeetCode–131. 分割回文串
动态规划解法：131. 分割回文串 | 手写图解版思路 + 代码讲解

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。返回 s 所有可能的分割方案。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]

回溯+正反序判断回文串

其实切割问题类似组合问题。

例如对于字符串 abcdef：

组合问题：选取一个 a 之后，在 bcdef 中再去选取第二个，选取 b 之后在 cdef 中在选组第三个…。
切割问题：切割一个 a 之后，在 bcdef 中再去切割第二段，切割 b 之后在 cdef 中在切割第三段…。

所以切割问题，也可以抽象为一棵树形结构，如图：

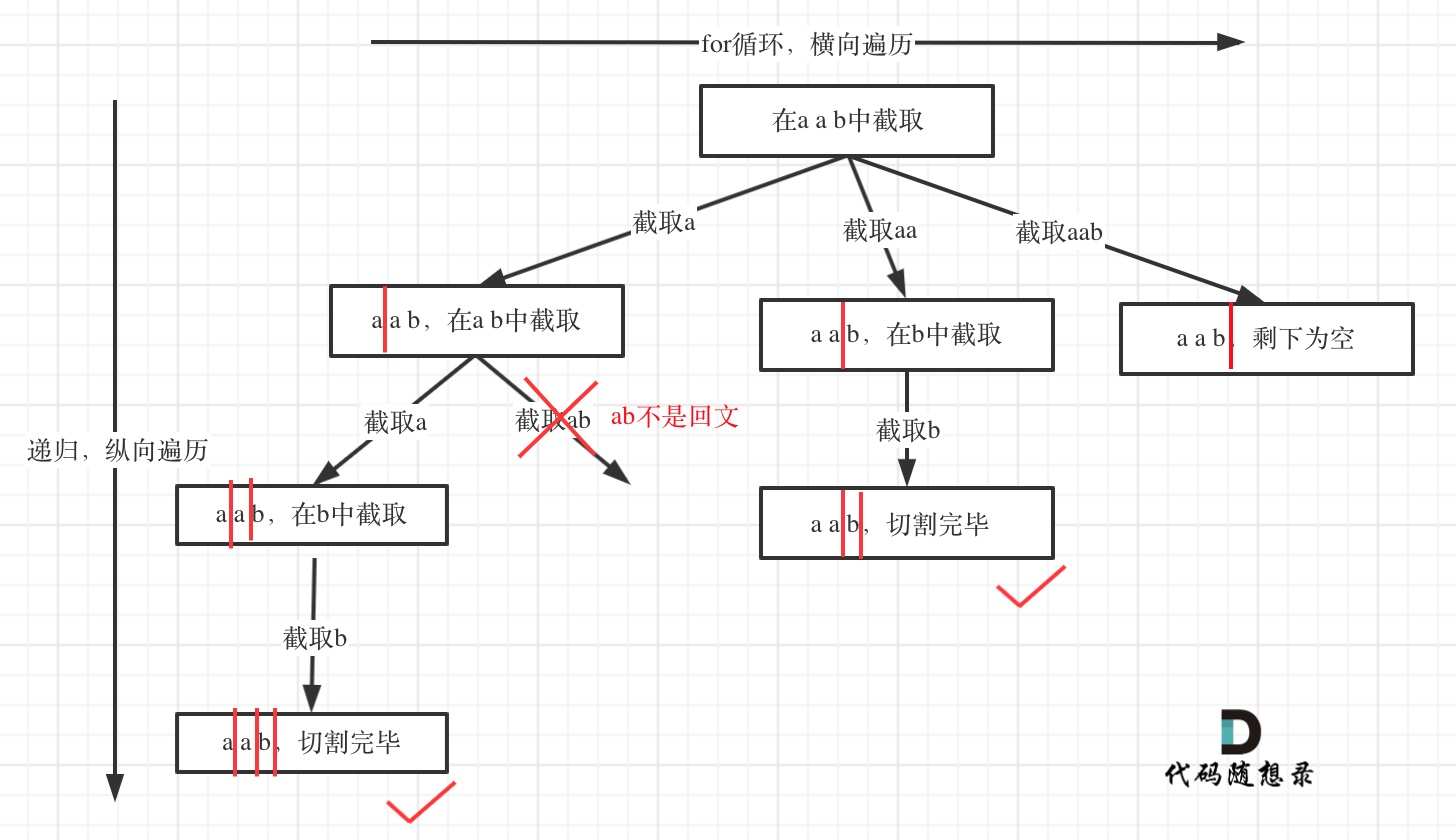
递归用来纵向遍历，for 循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。

此时可以发现，切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。

java

import java.util.ArrayList;
import java.util.List;
public class LeetCode_131_backtrack {
    public static void main(String[] args) {
        String s = "aab";
        System.out.println(partition(s));
    }


    public static List<List<String>> paths = new ArrayList<>();
    public static List<String> path = new ArrayList<>();


    public static List<List<String>> partition(String s) {
        backtrack(s, 0);
        return paths;
    }


    public static void backtrack(String s, int startIndex) {
        int n = s.length();
        // 递归出口，startIndex >= n
        if (startIndex >= n) {
            paths.add(new ArrayList<>(path));
            return;
        }
        // 横向遍历，每个元素作为起点，划分出来的每个字符串是回文串
        for (int i = startIndex; i < n; i++) {
            String cur = s.substring(startIndex, i + 1);
            // 判断当前划分是否回文
            if (!cur.contentEquals(new StringBuilder(cur).reverse())) {
                continue;
            }
            path.add(cur);
            // 纵向遍历，从下一个元素开始寻找下一个回文子串
            backtrack(s, i + 1);
            // 回溯，当前路径遍历结束
            path.removeLast();
        }
    }
}

python

class Solution:
    def __init__(self):
        self.paths = []
        self.path = []
    def partition(self, s: str):
        '''
        递归用于纵向遍历
        for 循环用于横向遍历
        当切割线迭代至字符串末尾，说明找到一种方法
        类似组合问题，为了不重复切割同一位置，需要 start_index 来做标记下一轮递归的起始位置(切割线)
        '''
        self.path.clear()
        self.paths.clear()
        self.backtracking(s, 0)
        return self.paths
        
    def backtracking(self, s, start_index):
        # Base Case
        if start_index >= len(s):
            self.paths.append(self.path[:])
            return
        # 单层递归逻辑
        for i in range(start_index, len(s)):
            # 此次比其他组合题目多了一步判断：
            # 判断被截取的这一段子串([start_index, i])是否为回文串
            temp = s[start_index:i + 1]
            if temp == temp[::-1]:  # 若反序和正序相同，意味着这是回文串
                self.path.append(temp)
                self.backtracking(s, i + 1)  # 递归纵向遍历：从下一处进行切割，判断其余是否仍为回文串
                self.path.pop()
            else:
                continue

回溯+函数判断回文串

class Solution:
    def __init__(self):
        self.paths = []
        self.path = []
    def partition(self, s):
        '''
        递归用于纵向遍历
        for 循环用于横向遍历
        当切割线迭代至字符串末尾，说明找到一种方法
        类似组合问题，为了不重复切割同一位置，需要 start_index 来做标记下一轮递归的起始位置(切割线)
        '''
        self.path.clear()
        self.paths.clear()
        self.backtracking(s, 0)
        return self.paths
        
    def backtracking(self, s, start_index):
        # Base Case
        if start_index >= len(s):
            self.paths.append(self.path[:])
            return
        # 单层递归逻辑
        for i in range(start_index, len(s)):
            # 此次比其他组合题目多了一步判断：
            # 判断被截取的这一段子串([start_index, i])是否为回文串
            if self.is_palindrome(s, start_index, i):
                self.path.append(s[start_index:i + 1])
                self.backtracking(s, i + 1)  # 递归纵向遍历：从下一处进行切割，判断其余是否仍为回文串
                self.path.pop()  # 回溯
            else:
                continue
    def is_palindrome(self, s, start, end):
        i: int = start
        j: int = end
        while i < j:
            if s[i] != s[j]:
                return False
            i += 1
            j -= 1
        return True

9、93.复原 IP 地址

参考：LeetCode–93. 复原 IP 地址

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。有效的 IP 地址正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。

例如：“0.1.2.201” 和 “192.168.1.1” 是有效的 IP 地址，但是 “0.011.255.245”、“192.168.1.312” 和 “192.168@1.1” 是无效的 IP 地址。

示例 1：

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

示例 2：

输入：s = "0000"
输出：["0.0.0.0"]

示例 3：

输入：s = "1111"
输出：["1.1.1.1"]

示例 4：

输入：s = "010010"
输出：["0.10.0.10","0.100.1.0"]

示例 5：

输入：s = "101023"
输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

递归

只要意识到这是切割问题，切割问题就可以使用回溯搜索法把所有可能性搜出来。切割问题可以抽象为树型结构，如图：

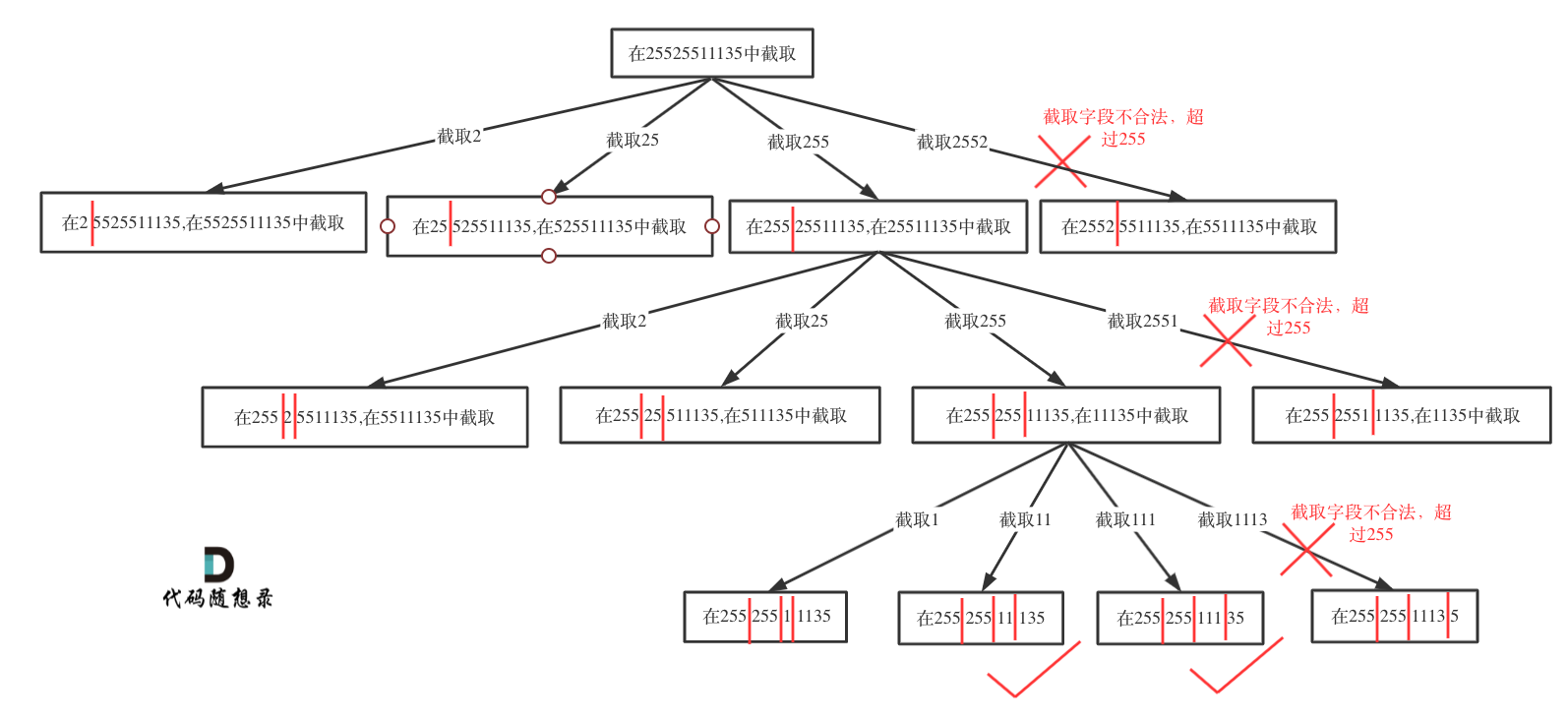
递归和回溯的过程：

递归调用时，下一层递归的 startIndex 要从 i+2 开始（因为需要在字符串中加入了分隔符.），同时记录分割符的数量 pointNum 要 +1。

回溯的时候，就将刚刚加入的分隔符. 删掉就可以了，pointNum 也要-1。

判断子串是否合法

最后就是在写一个判断段位是否是有效段位了。

主要考虑到如下三点：

段位以 0 为开头的数字不合法
段位里有非正整数字符不合法
段位如果大于 255 了不合法

java

import java.util.ArrayList;
import java.util.List;
public class LeetCode_93_backtrack {
    public static void main(String[] args) {
        String s = "25525511135";
        System.out.println(restoreIpAddresses(s));
    }


    public static List<String> paths = new ArrayList<>();
    public static List<String> path = new ArrayList<>();


    public static List<String> restoreIpAddresses(String s) {
        backtrack(s, 0);
        return paths;
    }


    public static void backtrack(String s, int startIndex) {
        int n = s.length();
        // 递归出口，startIndex >= n
        if (startIndex >= n) {
            String tmp = String.join(".", path);
            if (tmp.length() - 3 == n) {
                paths.add(tmp);
            }
            return;
        }
        // 横向遍历，以每一个元素作为起点，同时需要符合ip地址规范：0-256、多个字符不以0开头
        for (int i = startIndex; i < n; i++) {
            String cur = s.substring(startIndex, i + 1);
            // 判断当前划分是否符合ip地址规范
            if (cur.length() > 3 || Integer.parseInt(cur) > 255 || (cur.length() > 1 && cur.charAt(0) == '0')) {
                return;
            }
            path.add(cur);
            // 纵向遍历，下一个元素开始遍历
            backtrack(s, i + 1);
            // 回溯，当前ip地址划分结束
            path.removeLast();
        }
    }
}

python

class Solution:
    def __init__(self):
        self.result = []
    def restoreIpAddresses(self, s: str) -> list:
        '''
        本质切割问题使用回溯搜索法，本题只能切割三次，所以纵向递归总共四层
        因为不能重复分割，所以需要 start_index 来记录下一层递归分割的起始位置
        添加变量 point_num 来记录逗号的数量[0,3]
        '''
        self.result.clear()
        if len(s) > 12: return []
        self.backtracking(s, 0, 0)
        return self.result
        
    def backtracking(self, s: str, start_index: int, point_num: int) -> None:
        # Base Case
        if point_num == 3:
            if self.is_valid(s, start_index, len(s) - 1):
                self.result.append(s[:])
            return
        # 单层递归逻辑
        for i in range(start_index, len(s)):
            # [start_index, i]就是被截取的子串
            if self.is_valid(s, start_index, i):
                s = s[:i + 1] + '.' + s[i + 1:]
                self.backtracking(s, i + 2, point_num + 1)  # 在填入.后，下一子串起始后移 2 位
                s = s[:i + 1] + s[i + 2:]  # 回溯
            else:
                # 若当前被截取的子串大于 255 或者大于三位数，直接结束本层循环
                break
    def is_valid(self, s: str, start: int, end: int) -> bool:
        if start > end: return False
        # 若数字是 0 开头，不合法
        if s[start] == '0' and start != end:
            return False
        if not 0 <= int(s[start:end + 1]) <= 255:
            return False
        return True

四、子集问题

10、78.子集

参考：LeetCode–78 . 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

递归

如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！

其实子集也是一种组合问题，因为它的集合是无序的，子集{1,2} 和子集{2,1}是一样的。

那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for 就要从 startIndex 开始，而不是从 0 开始！

以示例中 nums = [1,2,3]为例把求子集抽象为树型结构，如下：

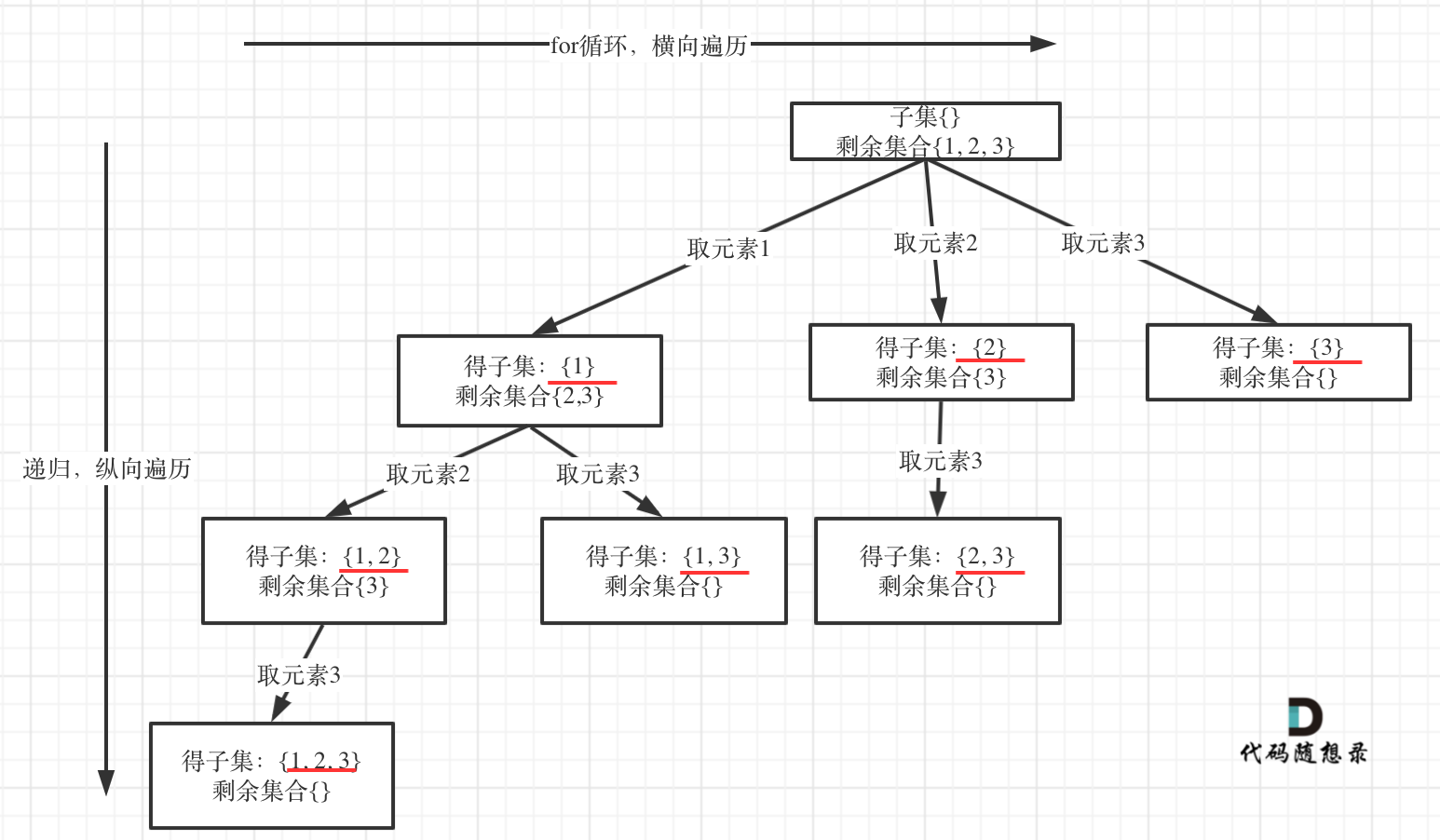
从图中红线部分，可以看出遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合

java

import java.util.ArrayList;
import java.util.List;
public class LeetCode_78_backtrack {
    public static void main(String[] args) {
        int[] nums = {1, 2, 3};
        System.out.println(subsets(nums));
    }


    public static List<List<Integer>> paths = new ArrayList<>();
    public static List<Integer> path = new ArrayList<>();


    public static List<List<Integer>> subsets(int[] nums) {
        backtrack(nums, 0);
        return paths;
    }


    public static void backtrack(int[] nums, int startIndex) {
        int n = nums.length;
        // 记录每一次path的中间过程，即子集
        paths.add(new ArrayList<>(path));
        // 递归出口，startIndex >= n
        if (startIndex >= n) {
            return;
        }


        // 横向遍历，以每一个元素为起点
        for (int i = startIndex; i < n; i++) {
            path.add(nums[i]);
            // 纵向遍历，从下一个元素开始获取下一层的元素
            backtrack(nums, i + 1);
            // 回溯，当前路径遍历结束
            path.removeLast();
        }
    }
}

复杂度分析

时间复杂度：O(n×2^n)。一共 2^n 个状态，每种状态需要 O(n) 的时间来构造子集。
空间复杂度：O(n)。临时数组 t 的空间代价是 O(n)，递归时栈空间的代价为 O(n)。

python

class Solution:
    def __init__(self):
        self.path: list = []
        self.paths: list = []
    def subsets(self, nums: list) -> list:
        self.paths.clear()
        self.path.clear()
        self.backtracking(nums, 0)
        return self.paths
        
    def backtracking(self, nums: list, start_index: int) -> None:
        # 收集子集，要先于终止判断
        self.paths.append(self.path[:])
        # Base Case
        if start_index == len(nums):
            return
        # 单层递归逻辑
        for i in range(start_index, len(nums)):
            self.path.append(nums[i])
            self.backtracking(nums, i+1)
            self.path.pop()     # 回溯

11、90.子集 II

参考：LeetCode–90. 子集 II

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例 1：

输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

递归

集合里有重复元素了，而且求取的子集要去重。理解“树层去重”和“树枝去重”非常重要

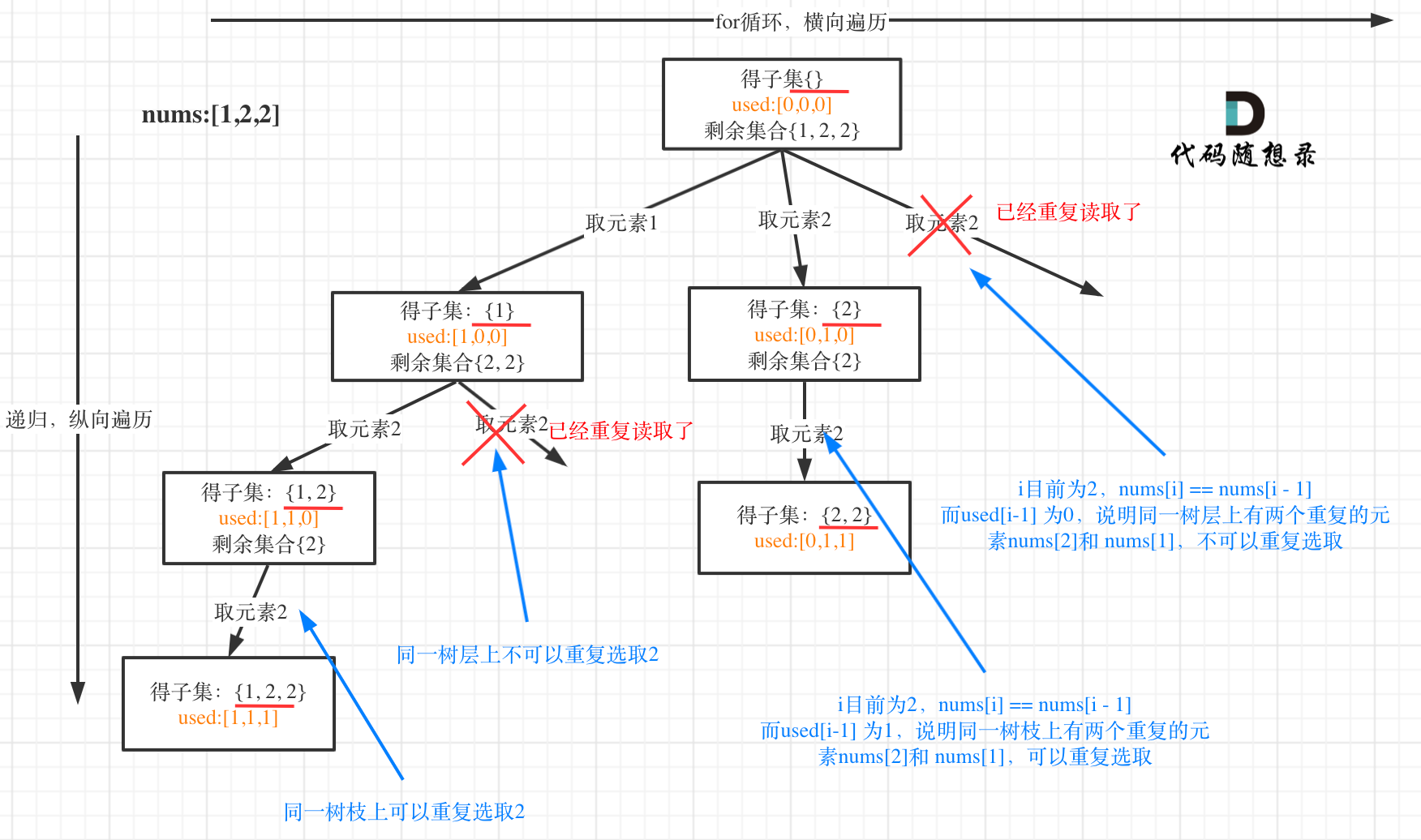
从图中可以看出，同一树层上重复取 2 就要过滤掉，同一树枝上就可以重复取 2，因为同一树枝上元素的集合才是唯一子集！

java

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class LeetCode_90_backtrack {
    public static void main(String[] args) {
        int[] nums = {1, 2, 2};
        System.out.println(subsetsWithDup(nums));
    }


    public static List<List<Integer>> paths = new ArrayList<>();
    public static List<Integer> path = new ArrayList<>();


    public static List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        backtrack(nums, 0);
        return paths;
    }


    public static void backtrack(int[] nums, int startIndex) {
        int n = nums.length;
        // 记录path的中间过程，即子集
        paths.add(new ArrayList<>(path));
        // 递归出口，startIndex >= n
        if (startIndex >= n) {
            return;
        }


        // 横向遍历，以每个元素作为起点，同一层重复的结点跳过
        for (int i = startIndex; i < n; i++) {
            if (i > startIndex && nums[i] == nums[i - 1]) {
                continue;
            }
            path.add(nums[i]);
            // 纵向遍历，从下一个元素开始遍历下一层结点
            backtrack(nums, i + 1);
            // 回溯，当前路径遍历结束
            path.removeLast();
        }
    }
}

复杂度分析

时间复杂度：O(n×2^n)，其中 n 是数组 nums 的长度。排序的时间复杂度为 O(nlogn)。最坏情况下 nums 中无重复元素，需要枚举其所有 2^n 个子集，每个子集加入答案时需要拷贝一份，耗时 O(n)，一共需要 O(n×2^{n)+O(n)=O(n×2}n) 的时间来构造子集。由于在渐进意义上 O(nlogn) 小于 O(n×2^n)，故总的时间复杂度为 O(n×2^n)。
空间复杂度：O(n)。临时数组 t 的空间代价是 O(n)，递归时栈空间的代价为 O(n)。

python

class Solution:
    def __init__(self):
        self.paths = []
        self.path = []
    def subsetsWithDup(self, nums: list) -> list:
        nums.sort()
        self.backtracking(nums, 0)
        return self.paths
        
    def backtracking(self, nums: list, start_index: int) -> None:
        # ps.空集合仍符合要求
        self.paths.append(self.path[:])
        # Base Case
        if start_index == len(nums):
            return
        # 单层递归逻辑
        for i in range(start_index, len(nums)):
            if i > start_index and nums[i] == nums[i - 1]:
                # 当前后元素值相同时，跳入下一个循环，去重
                continue
            self.path.append(nums[i])
            self.backtracking(nums, i + 1)
            self.path.pop()

12、491.非递减子序列

参考：LeetCode–491. 非递减子序列

给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是 2。

示例 1：

输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

输入：nums = [4,4,3,2,1]
输出：[[4,4]]

思路

求自增子序列，是不能对原数组经行排序的，排完序的数组都是自增子序列了。所以不能使用之前的去重逻辑！

本题给出的示例，还是一个有序数组 [4, 6, 7, 7]，这更容易误导大家按照排序的思路去做了。为了有鲜明的对比，我用[4, 7, 6, 7]这个数组来举例，抽象为树形结构如图：

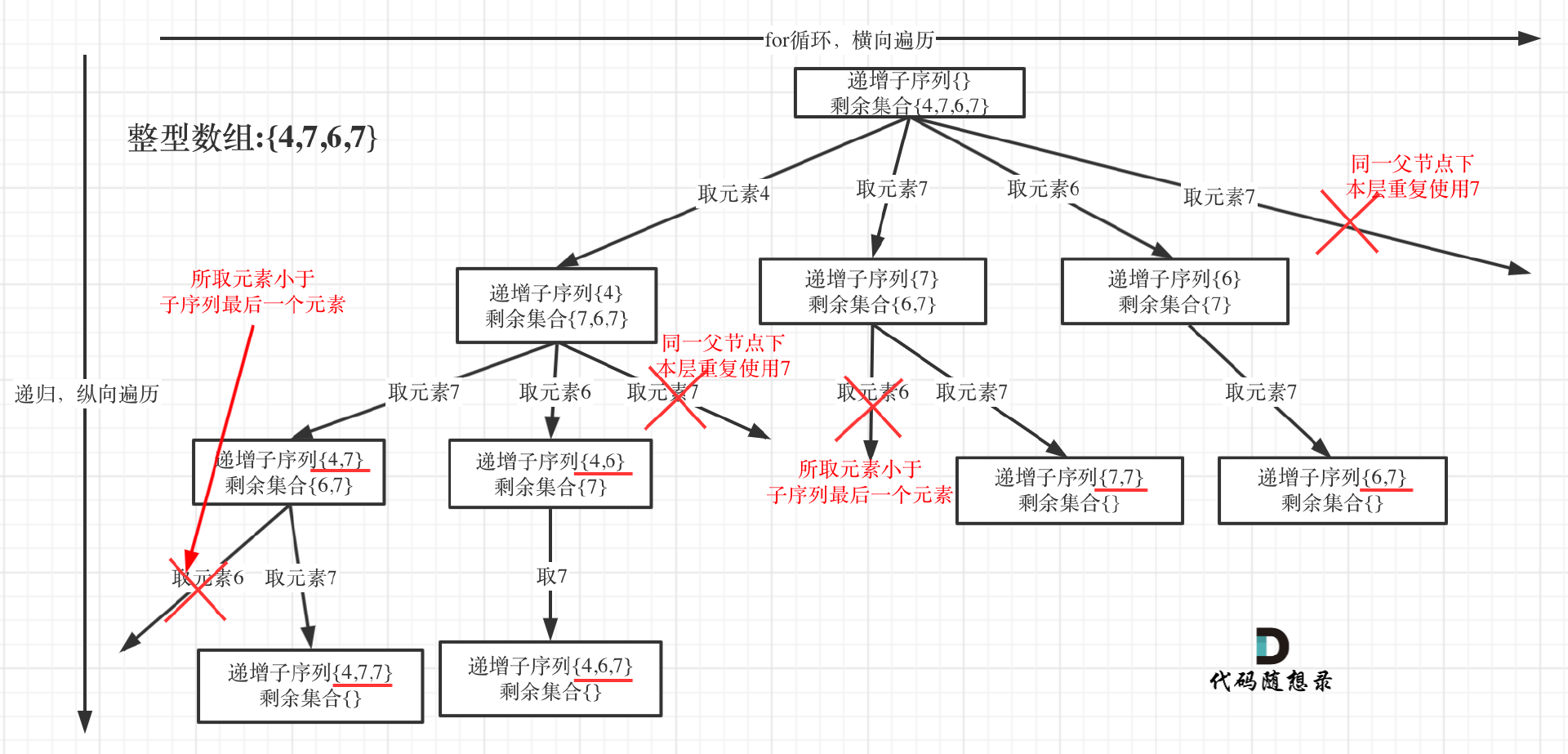
回溯

java

import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.Set;
public class LeetCode_491_backtrack {
    public static void main(String[] args) {
        int[] nums = {4, 6, 7, 7};
        System.out.println(findSubsequences(nums));
    }


    public static List<List<Integer>> paths = new ArrayList<>();
    public static List<Integer> path = new ArrayList<>();


    public static List<List<Integer>> findSubsequences(int[] nums) {
        backtrack(nums, 0);
        return paths;
    }


    public static void backtrack(int[] nums, int startIndex) {
        // 记录path的中间过程，即子集
        if (path.size() >= 2) {
            paths.add(new ArrayList<>(path));
        }
        // 递归出口，startIndex >= n
        int n = nums.length;
        if (startIndex >= n) {
            return;
        }


        Set<Integer> visited = new HashSet<>();
        // 横向遍历，以每个元素为起点，同一层相同的元素跳过（未排序数组），保证子集升序
        for (int i = startIndex; i < n; i++) {
            if ((!path.isEmpty() && nums[i] < path.getLast()) || visited.contains(nums[i])) {
                continue;
            }
            visited.add(nums[i]);
            path.add(nums[i]);
            backtrack(nums, i + 1);
            path.removeLast();
        }
    }
}

复杂度分析

时间复杂度：O(2^n *n)。仍然需要对子序列做二进制枚举，枚举出的序列虽然省去了判断合法性和哈希的过程，但是仍然需要 O(n) 的时间添加到答案中。
空间复杂度：O(n)。这里临时数组的空间代价是 O(n)，递归使用的栈空间的空间代价也是 O(n)。

python

class Solution:
    def __init__(self):
        self.paths = []
        self.path = []
    def findSubsequences(self, nums: list) -> list:
        '''
        本题求自增子序列，所以不能改变原数组顺序
        '''
        self.backtracking(nums, 0)
        return self.paths
        
    def backtracking(self, nums: list, start_index: int):
        # 收集结果，仍要置于终止条件之前
        if len(self.path) >= 2:
            # 本题要求所有的节点
            self.paths.append(self.path[:])
        # Base Case（可忽略）
        if start_index == len(nums):
            return
        # 单层递归逻辑
        # 深度遍历中每一层都会有一个全新的 usage_list 用于记录本层元素是否重复使用
        usage_list = set()
        # 同层横向遍历
        for i in range(start_index, len(nums)):
            # 若当前元素值小于前一个时（非递增）或者曾用过，跳入下一循环
            if (self.path and nums[i] < self.path[-1]) or nums[i] in usage_list:
                continue
            usage_list.add(nums[i])
            self.path.append(nums[i])
            self.backtracking(nums, i + 1)
            self.path.pop()

回溯+哈希表去重

class Solution:
    def __init__(self):
        self.paths = []
        self.path = []
    def findSubsequences(self, nums: list) -> list:
        '''
        本题求自增子序列，所以不能改变原数组顺序
        '''
        self.backtracking(nums, 0)
        return self.paths
        
    def backtracking(self, nums: list, start_index: int):
        # 收集结果，同 78.子集，仍要置于终止条件之前
        if len(self.path) >= 2:
            # 本题要求所有的节点
            self.paths.append(self.path[:])
        # Base Case（可忽略）
        if start_index == len(nums):
            return
        # 单层递归逻辑
        # 深度遍历中每一层都会有一个全新的 usage_list 用于记录本层元素是否重复使用
        usage_list = [False] * 201  # 使用列表去重，题中取值范围[-100, 100]
        # 同层横向遍历
        for i in range(start_index, len(nums)):
            # 若当前元素值小于前一个时（非递增）或者曾用过，跳入下一循环
            if (self.path and nums[i] < self.path[-1]) or usage_list[nums[i] + 100] == True:
                continue
            usage_list[nums[i] + 100] = True
            self.path.append(nums[i])
            self.backtracking(nums, i + 1)
            self.path.pop()

六、其他

13、332.重新安排行程

参考：LeetCode–332. 重新安排行程

给定一个机票的字符串二维数组 [from, to]，子数组中的两个成员分别表示飞机出发和降落的机场地点，对该行程进行重新规划排序。所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。

提示：

如果存在多种有效的行程，请你按字符自然排序返回最小的行程组合。例如，行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小，排序更靠前
所有的机场都用三个大写字母表示（机场代码）。
假定所有机票至少存在一种合理的行程。
所有的机票必须都用一次且只能用一次。

示例 1：

输入：tickets = [["MUC","LHR"],["JFK","MUC"],["SFO","SJC"],["LHR","SFO"]]
输出：["JFK","MUC","LHR","SFO","SJC"]

示例 2：

输入：tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
输出：["JFK","ATL","JFK","SFO","ATL","SFO"]
解释：另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"] ，但是它字典排序更大更靠后。

回溯

这道题目有几个难点：

一个行程中，如果航班处理不好容易变成一个圈，成为死循环
有多种解法，字母序靠前排在前面，让很多同学望而退步，如何该记录映射关系呢？
使用回溯法（也可以说深搜）的话，那么终止条件是什么呢？
搜索的过程中，如何遍历一个机场所对应的所有机场。

如何理解死循环

对于死循环，我来举一个有重复机场的例子：

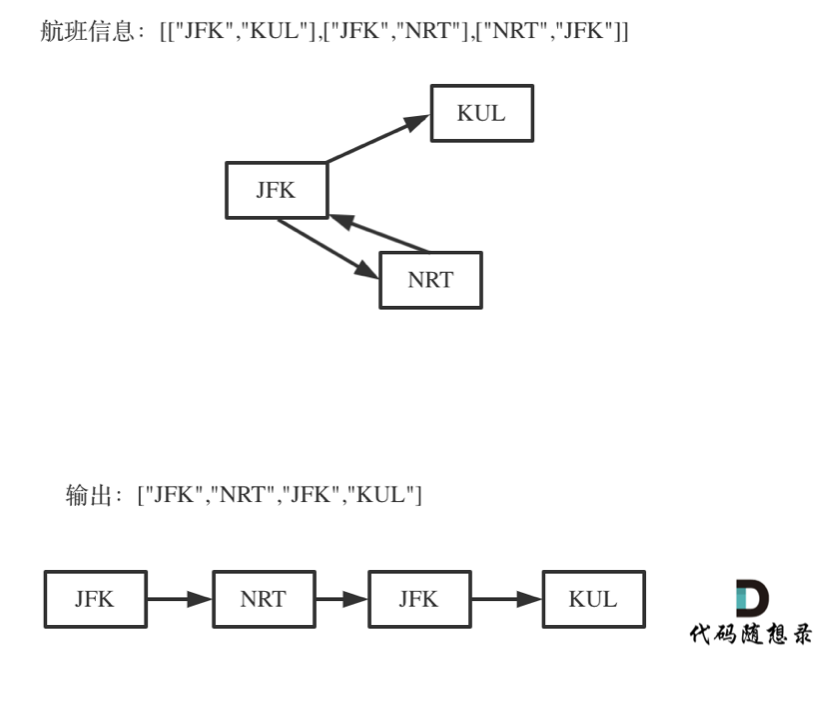
这个例子呢，就是告诉大家，出发机场和到达机场也会重复的，如果在解题的过程中没有对集合元素处理好，就会死循环。

tickets_dict：起点对应的终点集合，为了方便记录遍历过程中走过的路径和未走过的路径；

终止条件：遍历过程第一次找到路径点数=路径边+1 的路径，说明所有边都包含在路径中；

多种解法选取：tickets_dict 在使用前进行升序排序，可以保证回溯遍历过程中最先找到的路径是最终答案，即可停止遍历；

python

from collections import defaultdict
def findItinerary(tickets: list) -> list:
    # defaultdic(list) 是为了方便直接 append
    tickets_dict = defaultdict(list)
    for item in tickets:
        tickets_dict[item[0]].append(item[1])
    '''
    tickets_dict 里面的内容是这样的
     {'JFK': ['SFO', 'ATL'], 'SFO': ['ATL'], 'ATL': ['JFK', 'SFO']})
    '''
    path = ["JFK"]
    
    def backtracking(start_point):
        # 终止条件
        if len(path) == len(tickets) + 1:
            return True
        tickets_dict[start_point].sort()
        for _ in tickets_dict[start_point]:
            # 必须及时删除，避免出现死循环
            end_point = tickets_dict[start_point].pop(0)
            path.append(end_point)
            # 只要找到一个就可以返回了
            if backtracking(end_point):
                return True
            path.pop()
            tickets_dict[start_point].append(end_point)
            
    backtracking("JFK")
    return path

七、棋盘问题

14、51.N 皇后

LeetCode-- 51. N 皇后

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。给你一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个不同的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例 1：

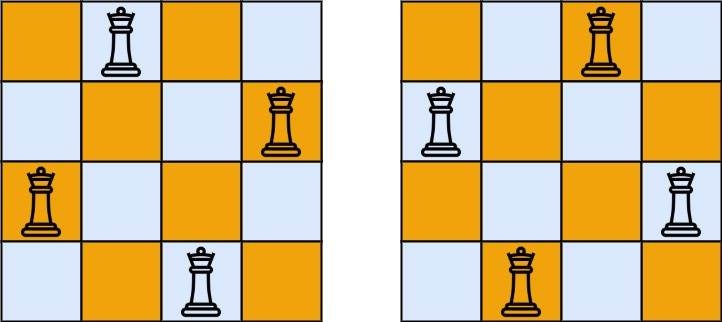
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

思路

首先来看一下皇后们的约束条件：

不能同行
不能同列
不能同斜线

确定完约束条件，来看看究竟要怎么去搜索皇后们的位置，其实搜索皇后的位置，可以抽象为一棵树。

下面我用一个 3 * 3 的棋盘，将搜索过程抽象为一棵树，如图：

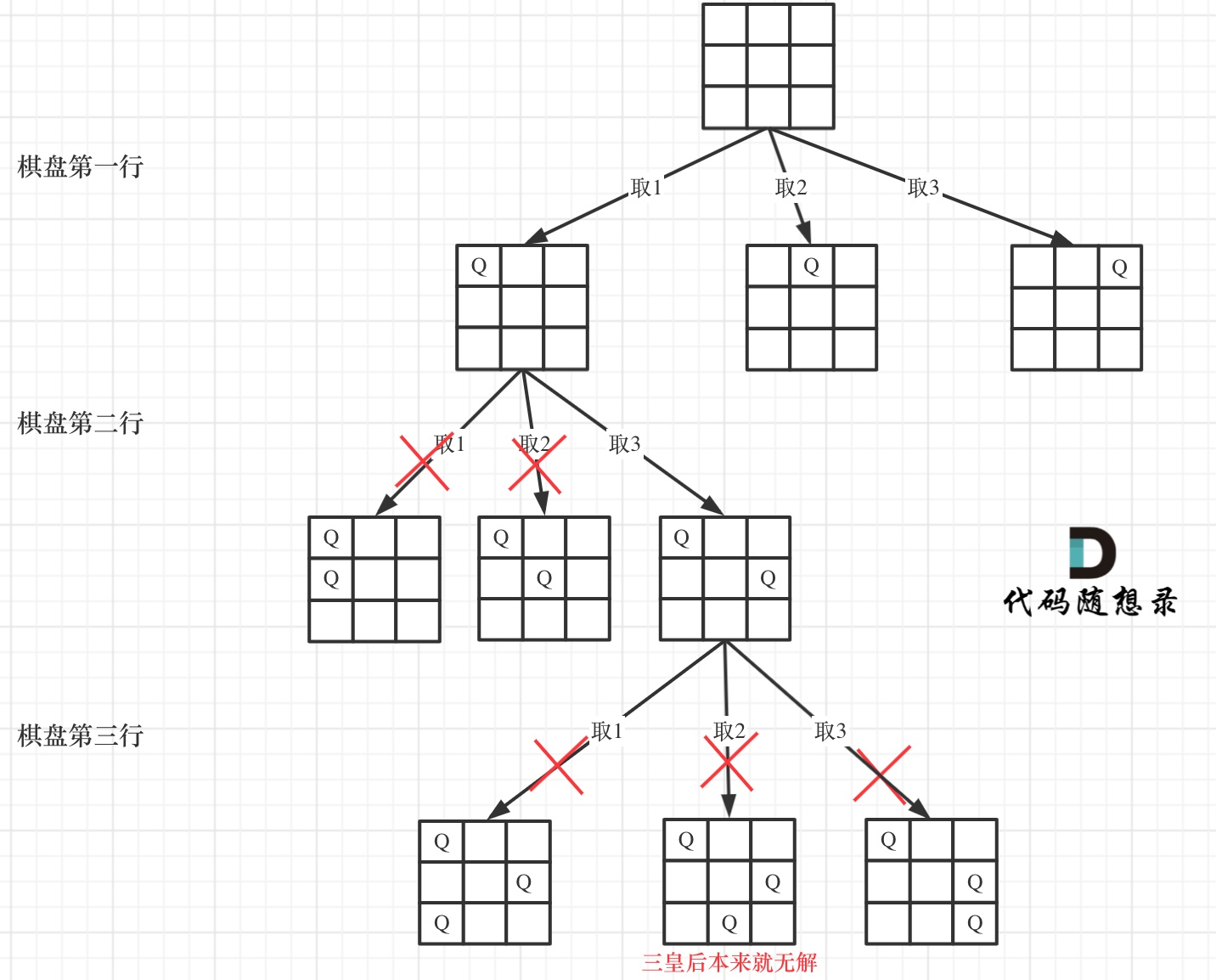
从图中，可以看出，二维矩阵中矩阵的高就是这棵树的高度，矩阵的宽就是树形结构中每一个节点的宽度。

那么我们用皇后们的约束条件，来回溯搜索这棵树，只要搜索到了树的叶子节点，说明就找到了皇后们的合理位置了。

回溯解法

def solveNQueens(n: int) -> list:
    if not n: return []
    board = [['.'] * n for _ in range(n)]
    res = []
    
    def isVaild(board, row, col):
        # 判断同一列是否冲突
        for i in range(len(board)):
            if board[i][col] == 'Q':
                return False
        # 判断左上角是否冲突(45 度角)
        i = row - 1
        j = col - 1
        while i >= 0 and j >= 0:
            if board[i][j] == 'Q':
                return False
            i -= 1
            j -= 1
        # 判断右上角是否冲突(135 度角)
        i = row - 1
        j = col + 1
        while i >= 0 and j < len(board):
            if board[i][j] == 'Q':
                return False
            i -= 1
            j += 1
        return True
        
    def backtracking(board, row, n):
        # 如果走到最后一行，说明已经找到一个解
        if row == n:
            temp_res = []
            for temp in board:
                temp_str = "".join(temp)
                temp_res.append(temp_str)
            res.append(temp_res)
        for col in range(n):
            if not isVaild(board, row, col):
                continue
            board[row][col] = 'Q'
            backtracking(board, row + 1, n)
            board[row][col] = '.'
            
    backtracking(board, 0, n)
    return res